Численное решение уравнений биокинетики в курсах «Общая экология» и «Моделирование биологических процессов»

Модель «хищник-жертва»

Обозначим через b1 и b2 популяцию (на момент времени t) зайцев и лис соответственно. Модель «хищник-жертва» утверждает, что b1 и b2 удовлетворяют системе

r1, r2, r3 и r4 – некоторые константы, например r1 = 2, r2 = 0.02, r3 = 0.0002 и r4 = 0.8. Решение ищется на некотором интервале t, например, [0; 5], причем в начальный момент времени имеется известное количество зайцев и лис, например, 5000 и 100, соответственно [Мэтьюз и Финк, 2001, с. 533–534]. Сравнивая эту модель с общей формой (1), замечаем следующее:

1. В данной конкретной модели рассматриваются только переменные и уравнения, характеризующие концентрации организмов, но нет переменных (cj ), описывающих концентрации веществ (и, следовательно, нет уравнений для них).
2. R1(b2) = r1 – r2 × b2 = 2 – 0.02 × b2; R2(b1) = –r3 + r4 × b1 = –0.0002 + 0.8 × b1; g1 = g2 = 0; θ = 5.
3. В уравнениях нет членов div(K × grad bi ) и div(v × bi ). С формальной точки зрения это может означать, что K = 0 и v = 0 или/и д2bi /дх2 = д2bi /ду2 = д2bi /дz2 = 0,
   дbi /дх = дbi /ду = дbi /дz = 0.
4. Поскольку, как было отмечено в предыдущем пункте, нет членов, описывающих перенос концентраций, то последние не будут изменяться в пространстве. Следовательно, пропадает смысл вообще вводить пространственные координаты х, область Q, ограничивающие ее поверхности Гk , а раз нет границ, то не будет и условий (2).
5. Начальные условия:

Распределенный брюсселятор

Рассмотрим систему

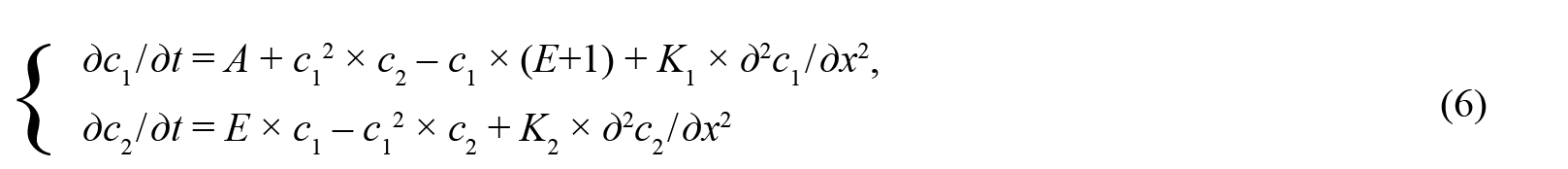
в области t>0, х∈(0, L), с начальными условиями

и условиями на границе отрезка (0, L)

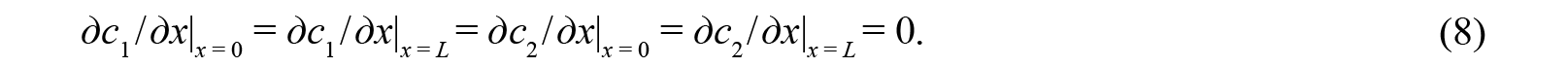
Эта система, описывающая многостадийную химическую реакцию с диффузией, была изучена в работах Пригожина и его школы (в Брюсселе [Ризниченко, 2011, с. 171]). Она дает модельное описание процессов, происходящих при дифференцировке тканей и морфогенезе [Рубин и др., 1987, с. 77–78]. Сравнивая модель (6)–(8) с общей формой (1)–(3), замечаем следующее:

1. В данной конкретной модели рассматриваются только переменные и уравнения, характеризующие концентрации веществ, но нет переменных (bi ), описывающих концентрации организмов (и, следовательно, нет уравнений для них).
2. W1(с1, с2) = А + c12 × c2 – c1 × (Е+1); W2(с1, с2) = Е × c1 – c12 × c2.
3. В уравнениях нет членов div(v × сj ). С формальной точки зрения это может означать, что v = 0.
4. Поскольку система одномерная, то div(Ki  × grad сi ) = д(Ki × дci /дх)/дх. В случае постоянного коэффициента диффузии, его можно вынести из оператора дифференцирования: д(Ki × дci /дх)/дх = Ki × д2ci /дх2. Заметим, что в данном примере K оказывается вектором, включающим в себя два элемента 14, ибо для вещества с1 характерен один коэффициент диффузии (K1), а для с2 – другой (K2).
5. Все функции ψjk  – нулевые; а операторы граничных условий Ĉjk  – это операторы дифференцирования: Ĉ11 = д/дх|х = 0 , Ĉ12 = д/дх|х = L , Ĉ21 = д/дх |х = 0; Ĉ22 = д/дх |х = L  (здесь мы полагали, что ось Х направлена слева направо и, таким образом, левую границу считали первой, правую – второй, т.е. k принимают значения 1 и 2, соответственно, для левой и правой границ).
6. Начальные условия (7) заданы как раз в форме (3).

Эффект Олли в стационарной распределенной системе

Следуя [Рубин и др., 1987, с. 76], рассмотрим в качестве очередного примера уравнение

в области х∈(0, L), с условиями на границе отрезка (0, L)

описывающее сильный эффект Олли 15.

В случае сильного эффекта Олли существует нижняя предельная численность (А), такая, что если популяция оказывается ниже этой численности, то скорость роста становится отрицательной, популяция вымирает (этот эффект можно интерпретировать как настолько низкую численность популяции, что репродукивные особи не находят друг друга в брачный сезон). Типичная форма учета сильного эффекта Олли имеет вид r × b × (b – А) × (1 – b/E). Таким образом, в соответствии с законами биологической кинетики мы должны были бы иметь для популяции в одномерной среде уравнение

дb/дt = D × д2b/дх2 + r × b × (b – А) × (1 – b/E),

где E – потенциальная емкость экологической системы [Братусь и др., 2010, с. 31, 332]; D – «коэффициент диффузии», отражающий, например, интенсивность перемещения организмов (в данном случае предполагается, что перемещение носит достаточно хаотический характер; а при четко выраженном таксисе уравнение будет другим). В стационарных условиях дb/дt = 0, поэтому

Полученное стационарное уравнение легко преобразовать к виду (9). Домножим (11) на E и разделим на r:

(E/r) × D × d2b/dх2 + b × (b – А) × (E – b) = 0.

Полученное уравнение в точности соответствует (9), если К = E × D/r.

Сравнивая модель (9)–(10) с общей формой (1)–(3), замечаем, следующее:

1. В данной конкретной модели рассматривается только переменная и уравнение 16, характеризующие концентрацию организмов, но нет переменных (сi ), описывающих концентрации веществ (и, следовательно, нет уравнений для них).
2. R1(b) = (b – А) × (E – b); g1(х, t) = 0.
3. В уравнении нет члена div(v × b). С формальной точки зрения это может означать, что v = 0.
4. Поскольку система одномерная, то div(K × grad b) = д(K × дb/дх)/дх. В случае постоянного коэффициента диффузии, его можно вынести из оператора дифференцирования: d(K × db/dх)/dх = K × d2b/dх2.
5. Все функции φik  – нулевые; а операторы граничных условий Âik  – это операторы дифференцирования: Â11 = д/дх|х = 0, Â12 = д/дх|х = L  (здесь мы полагали, что ось Х направлена слева направо и, таким образом, левую границу считали первой, правую – второй, т.е. k принимают значения 1 и 2, соответственно, для левой и правой границ).
6. Поскольку уравнение (9) описывает стационарную систему, то концентрация с течением времени меняться не будет (и нет члена дb/дt, описывающего это изменение). Следовательно, пропадает смысл вообще вводить начальные условия.

Прогноз качества воды

Рассмотрим, следуя Н.И. Дружинину и А.И. Шишкину [1989, с. 131], широко распространенное в практике инженерных расчетов прогноза качества воды дифференциальное уравнение в виде:

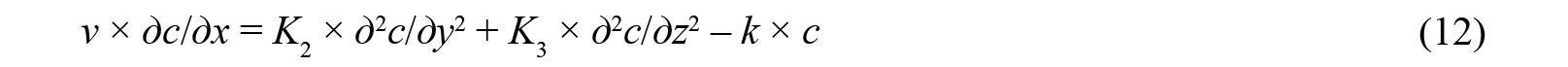
с граничными условиями второго рода

Сравнивая модель (12)–(13) с общей формой (1)–(3), замечаем следующее:

1. В данной конкретной модели рассматривается только переменная и уравнение 17, характеризующие концентрацию вещества, но нет переменных (bi ), описывающих концентрации организмов (и, следовательно, нет уравнений для них).
2. W1(с) = –k × c;
3. Член div(v × с) редуцирован до -v × дс/дх. С формальной точки зрения это может означать, что компонены вектора v таковы: v1 = –v, v2 = v3 = 0. А по физическому смыслу это соответствует конвективному переносу вдоль оси х (с постоянной скоростью) и отсутствию 18 такового по направлениям у и z.
4. Член div(K × grad c) редуцирован до K2 × д2c/ду2 + K3 × д2c/дz2. С формальной точки зрения это означает, что х-компонента вектора К – нулевая (или/и д2c/дх2 = 0), а две другие – постоянны, но различны. По физическому смыслу это соответствует отсутствию диффузионного переноса вдоль оси х и диффузионному транспорту с различающимися коэффициентами диффузии по направлениям у и z.
5. На первый взгляд мы имеем стационарное уравнение (типа 1.3.0 – см. рис. 1). Таким образом, концентрация с течением времени меняться не будет (и нет члена дb/дt, описывающего это изменение). Следовательно, пропадает смысл вообще вводить начальные условия. По физическому смыслу это, конечно, так. Но 
   с точки зрения математического формализма к данному уравнению можно подойти иначе. Если формально вместо «х» написать «t» 19, то (12) окажется относящимся к типу 1.2.1 (см. рис. 1). Поскольку в уравнении производная по х имеет первый порядок, то соответствующее краевое условие нужно задать только на одной границе. Если, например, известно распределение концентрации в плоскости yz, задаваемое некоторой функцией C1(y, z) то мы имеем начальное условие с(0, y, z) = C1(y, z).
6. На других границах задается по два граничных условия 2 –го рода.

Хемостат

Теория хемостата представляет собой одну из основных классических теорий микробиологической кинетики и подробно описана в литературе – см., например, [Перт, 1978, с. 43–74; Полуэктов с соавт., 1980, с. 73–81; Паников, 1992, с. 30–31; Глаголев и Смагин, 2005, с. 39–49]. Кратко коснемся истории разработки хемостата.

Впервые проточный способ культивирования был применен Виноградским для выращивания серобактерий еще в XIX в. Свежую питательную среду он вносил вручную порциями (несколько раз в день). Также вручную и дискретными порциями производилась подача свежей питательной среды при многолетнем непрерывном выращивании простейших в опытах Л. Вудрафа 20 [Паников, 1992, c. 29]. Но из-за дискретности подачи среды эти первые робкие попытки нельзя считать истинно хемостатным куьтивированием.

В 1920-е гг. появились первые культиваторы с истинно непрерывным поступлением питательной среды [Паников, 1992, c. 29]. Практически одновременно их создали Е.С. Haddon 21 и М.Д. Утёнков. Поскольку имя последнего оказалось, фактически, забыто в истории отечественной науки, сейчас мы бы хотели отчасти исправить эту несправедливость.

Михаил Дмитриевич Утёнков (1893–1953) был научным сотрудником Красной Советской больницы им. С.П. Галицкого 22. В 1929 г. он запатентовал 23 аппарат, названный им «микрогенератор», в 1939 г. защитил диссертацию 24 на тему «Микрогенерирование», а в 1941 г. опубликовал о нем книгу «Микрогенерирование» 25 (издательство «Советская наука») [Белокрысенко, 2014].

«Микрогенератор» давал возможность непрерывного культивирования микроорганизмов в изолированном стерильном сосуде – «культиваторе», – обеспеченном ручной системой непрерывного добавления свежей питательной среды, регулированием рН, аэрацией и оттоком избытка среды с культурой. В своей книге Михаил Дмитриевич представил не только описание и схему общего принципа работы аппарата, но и целый ряд техник и устройств, обеспечивающих стерильность работы, регулярный отбор проб из культиватора для микропрепаратов и посевов с 5- или 10-минутными промежутками, а также 6 вариантов моделей микрогенераторов, использованных им на практике и предназначенных для специальных исследований: автоматического изменения состава подаваемой жидкой среды, быстрого или постепенного, многократного изменения состава питательной среды и др. Среди прочих описана модель «газового микрогенератора» для работы с анаэробами и в атмосфере определённого газа. Что касается теории, то дан расчёт скорости подачи свежей питательной среды в культиватор с учётом времени генерации микроорганизмов. В книге приведен и ряд важных наблюдений: уменьшение времени генерации (для кишечной палочки – с 20 до 15 мин) с уменьшением размеров клеток, охарактеризованы взаимоотношения двух бактериальных видов, культивируемых одновременно. Также определены возможности практического использования техники непрерывного культивирования микроорганизмов: получение микробной массы (например, грибов), непрерывное получение продуктов бактериального синтеза, токсинов, получение «модифицированных» культур микроорганизмов путём длительного непрерывного культивирования при медленно изменяющихся условиях (температура, химические агенты) [Белокрысенко, 2014]. К сожалению, судьба изобретателя «микрогенератора»-хемостата сложилась трагически.

В 1944 г. Утёнков был исключён из ВКП(б), а в 1945 г. (в соответствии с приказом наркома здравоохранения СССР Т.А. Митерева) освобождён от должности зав. кафедрой с запрещением вести преподавательскую работу 26. С 1942 по 1948 г. М.Д. Утёнков заведовал также микробиологической лабораторией в Институте патологии и терапии интоксикаций АМН СССР. Но в 1948 г. лаборатория была ликвидирована, а он переведён на должность старшего научного сотрудника и затем – в Институт вирусологии АМН СССР, где утверждён в должности заведующего лабораторией геморрагических лихорадок 27 [Белокрысенко, 2014]. Однако в постановлении декабрьской 8 –ой сессии общего собрания АМН СССР было сказано о решении ликвидировать лабораторию Утёнкова. И можно предположить, что весной или летом 1953 г. она действительно была закрыта [Шаталкин, 2016, с. 162]. 28 августа 1953 г. М.Д. Утёнков и его жена Мария Казимировна Утёнкова покончили жизнь самоубийством (через повешение) [Белокрысенко, 2014].

Хемостатная культура – это полностью перемешиваемая суспензия биомассы, в которую с постоянной скоростью подается среда и из которой с той же скоростью отбирается культура; общий объем культуры остается постоянным. Увеличение концентрации биомассы дается уравнением баланса биомассы:

Общее увеличение биомассы = Рост – Отток.

Пусть b – концентрация биомассы, V и F – соответственно объем и скорость течения среды, а µ − удельная скорость роста (скорость роста единицы биомассы). Тогда для бесконечно малого промежутка времени dt для полной культуры этот баланс будет выглядеть следующим образом:

V × db = V × m × b × dt – F × b × dt.

Поделив это уравнение на V × dt, получим

Значение F/V = D известно как скорость разбавления [Перт, 1978, c. 44, 47].

Баланс для лимитирующего субстрата:

Общее увеличение = Поступление – Отток – Субстрат, использованный на рост.

Пусть sr  и c – концентрации субстрата соответственно на входе в хемостат и на выходе из него, а Y – экономический коэффициент [Перт, 1978, c. 47]. Тогда этот баланс можно выразить следующим образом:

V × dc = F × sr × dt – F × c × dt – V × m × b × dt /Y.

Следовательно,

Итак, модель динамики системы «хемостат» задана общими уравнениями (14), (15).

Если скорость вымывания биомассы вначале будет меньше максимальной скорости роста, то конценрация биомассы будет увеличиваться. Однако соответствующее уменьшение концентрации лимитирующего рост субстрата приведет к тому, что удельная скорость роста биомассы будет уменьшаться до тех пор, пока скорость роста биомассы не станет равной скорости вымывания. Дальнейших изменений в конценрации биомассы и лимитирующего субстрата не может быть [Перт, 1978, c. 46], следовательно, мы имеем стационарное состояние.

В стационарном состоянии db/dt = dc/dt = 0, тогда значения стационарных концентраций (bст, cст) даются уравнениями

(µ – D) × bст = 0,

D × (sr  – cст) – m × bст/Y = 0.

Но для возможности практического решения этих уравнений (для того, чтобы получить bст и cст) нужно подставить конкретное выражение для удельной скорости роста [Перт, 1978, c. 47] – ее зависимость от концентрации субстрата 28.

Для конкретного примера изберем функцию № 11 из [Бирюков и Кантере, 1985, с. 99]:

µ = mmax × c/[(KS +c) × ec/K].

Тогда система стационарных уравнений примет вид:

Сравнивая модель (16) с общей формой (1)–(3), замечаем, следующее:

1. В данной конкретной модели рассматривается по одной переменной для концентраций организмов и веществ (и, следовательно, по одному уравнению для них), поэтому мы не стали вводить подстрочные индексы для переменных, а ограничились обозначениями bст и сст.
2. R1(сст) = mmax × cст/[(KS +c) × eхр(cст/K)] – D; g1 = 0.
3. В уравнениях нет членов div(v × bст), div(v × cст), div(K × grad bст) и div(K × grad сст). Для данной системы это вполне естественно, поскольку хемостат представляет собой систему с полным перемешиванием, в результате которого достигаются одинаковые условия во всем объеме среды, следовательно, производные от cст и bст по пространственным координатам будут нулевыми.
4. Поскольку, как было отмечено в предыдущем пункте, нет членов, описывающих перенос концентраций, то последние не будут изменяться в пространстве. Следовательно, пропадает смысл вообще вводить пространственные координаты х, область Q, ограничивающие ее поверхности Гk , а раз нет границ, то не будет и условий (2) на этих границах.
5. Аналогично, поскольку система (16) описывает стационарную систему, то концентрации с течением времени меняться не будут (и нет членов дbст/дt, дсст/дt, описывающих эти изменения). Следовательно, пропадает смысл вообще вводить начальные условия.

То, что конкретные примеры моделей оказались существенно проще общей постановки задачи (1)–(3), наводит на следующую мысль: возможно, для этих частных случаев существуют более простые методы решения, чем универсальный метод для (1–3).

---