Робастное управление динамическими объектами

На рис. 3 представления обобщенная структурная схема системы управления [1, 13]. Она содержит матричный (многомерный) объект P, включающий в себя весовые функции, регулятор K и матричную неопределенность $\mathrm{\Delta }$. Векторный сигнал d содержит шумы, возмущения и задающие воздействия, e есть векторный сигнал, содержащий все управляемые сигналы и сигналы ошибок, u – сигнал управления, y – сигнал измерений, поступающий в обратную связь через регулятор K.

Блок-схема рис. 3 описывается следующей системой уравнений

$\left[\begin{array}{c}z\\ e\\ y\end{array}\right]=P \left[\begin{array}{c}v\\ d\\ u\end{array}\right], v=\mathrm{\Delta }z, u=Ky.$

Пусть передаточная матрица от d к e есть Tde, а приемлемая неопределенность удовлетворяет условию $\overline{\sigma }\left(\mathrm{\Delta }\right) < 1/{\gamma }_u$ для некоторого ${\gamma }_u > 0$.

Тогда проблема анализа состоит в том, чтобы получить ответ: является ли замкнутая система устойчива для всех приемлемых $\mathrm{\Delta }$ и удовлетворяется ли неравенство качества управления ${||T_{de}||}_{\infty }\le {\gamma }_p$ для заданного ${\gamma }_p > 0$.

Задача синтеза состоит: в проектировании регулятора , который бы удовлетворял вышеупомянутым условиям робастной устойчивости и качества управления.

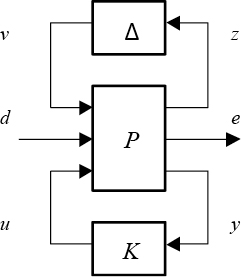
Рис. 3. Обобщенная структурная схема системы управления [1]

В зависимости от наличия или отсутствия входного сигнала d или неопределенности $\mathrm{\Delta }$ в схеме рис. 3 имеется четыре постановки задач устойчивости и управления.

Номинальная устойчивость (Nominal Stability). Система устойчива в отсутствии неопределенности в объекте $(d=0, \mathrm{\Delta }=0)$.

Номинальное качество управления (Nominal Performance). Система удовлетворяет спецификации на качество управления в отсутствии неопределенности в объекте $(d\ne 0, \mathrm{\Delta }=0)$.

Робастная устойчивость (Robust Stability). Система устойчива при всех возмущенных объектах относительно номинальной модели, включая наихудший случай неопределенности модели $(d=0, \mathrm{\Delta }\ne 0)$.

Робастное качество управления (Robust Performance). Система удовлетворяет спецификации на качество управления для всех возмущенных объектов относительно номинальной модели, включая наихудший случай неопределенности модели $(d\ne 0, \mathrm{\Delta }\ne 0)$.

На рис. 4 приведена структурная схема замкнутой системы, поясняющая принцип робастного управления [24, с. 62]. Здесь семейство объектов описывается множеством P, которое состоит из номинальной передаточной функции P0 с добавлением к ней множества передаточных функций $P={\left\{\mathrm{\Delta }{P}_i\right\}}_1^N$, характеризующих неопределенность модели объекта: $P={\left\{{\mathrm{P}}_0+\mathrm{\Delta }{P}_i\right\}}_1^N$. Робастный регулятор должен гарантировать устойчивость замкнутой системы и требуемое качество управления для любого представителя модели объекта из семейства $P$ в отличие от классического регулятора, который обеспечивает устойчивость и качество управления только для одного объекта.

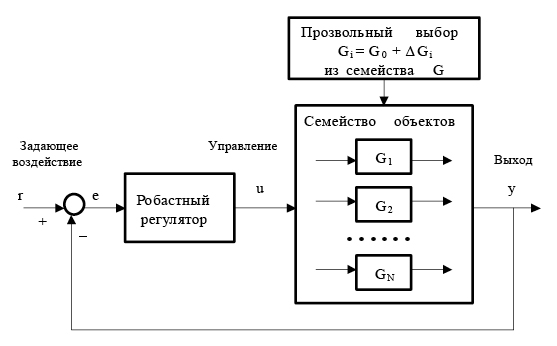
Рис. 4. Структурная схема робастной системы управления [24]