Робастное управление динамическими объектами

Компромисс между хорошим качеством управления и хорошей робастностью достигается посредством частотного разделения их при формулировании задачи смешанной чувствительности следующим образом.

Вначале взвешивают So и To с помощью весовых функций W1 и W3, а затем формируют передаточную функцию Tzd от возмущения d к фиктивному выходному сигналу

$z=\left[\begin{array}{c}{z}_1\\ z_2\end{array}\right], \mathrm{где} {\mathrm{z}}_1 = W_{1 }y, \mathrm{где} {\mathrm{z}}_2 = W_{3 }{y}_p$

(см. раздел 3 рис. 1):

$T_{zd }= \left[\begin{array}{cc}{W}_1& S_o\\ W_3& T_o\end{array}\right], {||T_{zd }||}_{\infty }\le 1.$

Для того, чтобы добиться минимального влияния возмущения d на выход z, нужно минимизировать $H_{\infty }-\mathrm{норму}$ передаточной функции системы с учетом ограничения 2-нормы выходного сигнала при действии на вход системы сигнала, ограниченного по 2-норме, согласно следующей лемме [6]:

Лемма. Если $w\in L_2$ и Z = Gw , то ${||z||}_2 \le {||G||}_{\infty }{||w||}_2$.

Доказательство

$$\begin{gathered} {||z||}_2^2 = \frac{1}{2\pi }{\int }_{-\infty }^{\infty }{||z\left(j\omega \right)||}^{2}d\omega = \frac{1}{2\pi }{\int }_{-\infty }^{\infty }{||G\left(j\omega \right)w\left(j\omega \right)||}^{2}d\omega \le \\ \le \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\overline{\sigma }\left(G\right(j\omega ){)}^2{||w\left(j\omega \right)||}^{2}d\omega \le \sup \overline{\sigma }(G\left(j\omega \right){)}^2 \frac{1}{2\pi }{\int }_{-\infty }^{\infty }{||w\left(j\omega \right)||}^{2}d\omega = {||G||}_{\infty }^2{||w||}_2^2 \end{gathered}$$

Тогда задача робастного управления ставится как задача H∞ оптимизации [2, 13]

(16) ${||T_{zd}(P,K)||}_{\infty } \underset{K}{\to } \min ,$

где K – принадлежит множеству внутренне стабилизирующих регуляторов. При этом матричные весовые функции $W_1\left(j\omega \right), W_3\left(j\omega \right)$

$\frac{1}{\overline{\sigma }\left[S_o\right(j\omega \left)\right]} \ge \overline{\sigma }\left[W_1\right(j\omega \left)\right],$ 

$\overline{\sigma }[ T_o (j\omega \left)\right] \le \underline{\sigma }\left[W_3^{-1}\right(j\omega \left)\right],$

выбираются так, чтобы задать границы области достижения желаемого качества управления (performance bound) и робастного запаса устойчивости (robustness bound) (рис. 2). Тогда на низких частотах

$\frac{1}{\overline{\sigma }\left[S_o\right(j\omega \left)\right]} \approx \overline{\sigma }\left[L_o\right(j\omega \left)\right] \ge \overline{\sigma }\left[W_1\right(j\omega \left)\right] \gg 1,$

а на высоких частотах

$\overline{\sigma }\left[S_o\right(j\omega \left)\right] \approx \overline{\sigma }\left[L_o\right(j\omega \left)\right] \le \underline{\sigma }\left[W_3^{-1}\right(j\omega \left)\right] \ll 1.$

Здесь использованы следующие неравенства [9]

$\underline{\sigma }\left(L_o\right)-1 \le \underline{\sigma }(L_o+I)\le \underline{\sigma }\left(L_o\right)+1,$

$\underline{\sigma }\left(L_o\right)-1 \le \frac{1}{\overline{\sigma }\left(S\right)} \le \underline{\sigma }\left(L_o\right)+1,$

$\underline{\sigma }\left(L_o\right) \gg 1 \Rightarrow \underline{\sigma }\left(L_o\right) \approx \frac{1}{\overline{\sigma }\left(S_o\right)}.$.

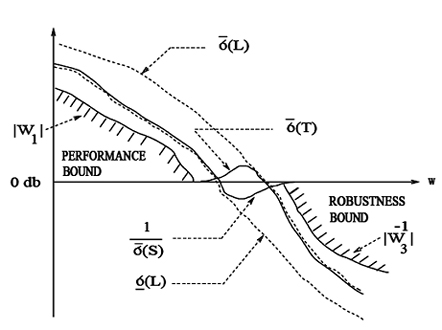
Рис. 2. Спецификация на So и To посредством частотных зависимостей сингулярных чисел [32].