Робастное управление динамическими объектами

3.1. Замкнутая система управления

3.2. Устойчивость

3.3. Слежение и стабилизация

3.4. Подавление выходного возмущения

3.5. Подавление шума

3.6. Робастность

***

3.1. Замкнутая система управления

На рис. 1 приведена стандартная конфигурация замкнутой системы управления. Она содержит модель объекта управления P и регулятор K, замкнутые отрицательной обратной связью. На систему воздействует задающее воздействие r(t), шум датчиков (ошибки измерений) n(t), возмущение на входе объекта di(t), возмущение на выходе объекта d(t). В общем случае предполагается, что система является многомерной: сигналы являются векторными функциями времени, а передаточные матрицы модели объекта P(s) и регулятора K(s) имеют соответствующие размеры.

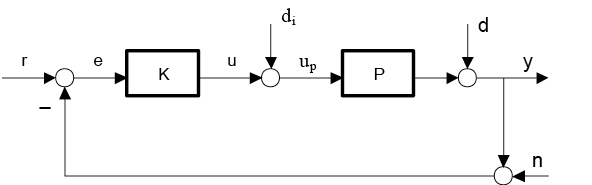
Рис. 1. Стандартная блок-схема замкнутой системы управления [13]

Введем основные матричные соотношения, связывающие различные сигналы замкнутой системы. Определим входную Li и выходную Lo матричные передаточные функции разомкнутой системы

Li = KP, Lo = PK,

где Li получается размыканием контура обратной связи на входе u объекта, а Lo – на выходе y объекта соответственно. Входная матричная передаточная функция чувствительности Si определяется как передаточная функция от di к up:

Si = (I+Li )–1, up = Sidi.

Выходная матричная передаточная функция чувствительности So преобразует сигнал d в y:

So = (I+Li )–1, up = Sidi.

Входная Ti и выходная To дополнительные матричные передаточные функции чувствительности определяются следующим образом:

Ti = I – Si = LiSi = SiLi ,
To = I – So = LoSo = SoLo .

Термин дополнительный используется для подчеркивания того факта, что To является дополнением к So, т.е.

To = I – So.

Это фундаментальное соотношение легко доказывается

So + To = (I + Lo)–1 + Lo (I + Lo)–1 = (I + Lo)(I + Lo)–1 = I.

Матрица $I+L_i$называется входной возвратной разностью, а матрица $I+L_o$ – выходной возвратной разностью.

Определение. Замкнутая система является корректной (хорошо обусловленной), если передаточные функции, преобразующие сигналы (r, di) в (e, up), являются правильными.

Из этих правильных передаточных функций могут быть получены все другие передаточные функции замкнутой системы, которые также будут правильными. Корректность определяется следующей леммой.

Лемма [6]. Пусть $P, K\in R{H}_{\infty }$. Тогда система на рис. 1 корректна, если и только если

(9) $\det [I+Lo(\infty \left)\right]\ne 0.$

Выполнение условия (9) означает реализуемость передаточных функций системы, т. к. каждый элемент правильных передаточных матриц имеет степень числителя не выше степени знаменателя. Входные сигналы (r, di, d, n) системы связаны с выходом y и внутренними сигналами (e, u, up) следующими соотношениями:

(10) y = To(r – n) + SoPdi + Sod,

(11) e = So(r – d – n) + SoPdi,

(12) u = KSo(r – d – n) + Tidi,

(13) up = KSo(r – d – n) + Sidi.

3.2. Устойчивость

Первое требование, которому должна удовлетворять замкнутая система – это устойчивость. Прежде всего, система должна быть устойчива относительно входа и выхода: передаточные матрицы, преобразующие (r, di, d, n) в y, должны быть устойчивы, что эквивалентно ограниченности выхода y при ограниченности входных сигналов (r, di, d, n). Часто требуется более сильное требование к устойчивости для того, чтобы обеспечить также ограниченность внутренних сигналов. Это приводит к следующему определению внутренней устойчивости.

Определение. Говорят, что система (рис. 1) внутренне устойчива, если передаточная функция от w, d к e, up устойчива.

Т. к. это условие обеспечивает устойчивость всех других передаточных функций системы, то ограниченные сигналы (r, di, d, n) вызывают ограниченные выход y и внутренние сигналы e, up.

Лемма [6]. Пусть $P, K\in R{H}_{\infty }$, тогда система с обратной связью на рис. 1 внутренне устойчива, если и только если

(14) ${\left[\begin{array}{cc}I& K\\ –P& I\end{array}\right]}^{–1}= \left[\begin{array}{cc}{S}_i& –K{S}_o\\ P{S}_i& S_o\end{array}\right] \in R{H}_{\infty }.$

3.3. Слежение и стабилизация

Одной из целей корректной и внутренне устойчивой системы управления, удовлетворяющей (9), (14), является слежение выхода y за задающим воздействием r. (Если r=const, то решается задача стабилизации). Из (11) следует, что So преобразует r в сигнал ошибки er = Sor. Тогда на любой частоте ω хорошее слежение может быть достигнуто при низкой выходной чувствительности, поскольку

$\frac{{\displaystyle {||e_r\left(j\omega \right)||}_2}}{{\displaystyle {||r\left(j\omega \right)||}_2}} \le \overline{\sigma } \left[S_o\left(j\omega \right)\right].$

Если So=0, то To=I и тогда возможно точное слежение во всем частотном диапазоне. Такое слежение требует большого коэффициента усиления разомкнутой системы $\underset{}{\underline{\sigma }} \left(L_o\right) \gg 1$. На практике это возможно только в ограниченном диапазоне частот.

3.4. Подавление выходного возмущения

Из (10) вытекает, что So преобразует d в компоненту yd = Sod. Тогда для ослабления действия выходного возмущения d на выход объекта y, необходимо также иметь малую величину выходной чувствительности

$\frac{{\displaystyle {||y_d\left(j\omega \right)||}_2}}{{\displaystyle {||d\left(j\omega \right)||}_2}} \le \overline{\sigma } \left[S_o\left(j\omega \right)\right].$

Слежение и подавление выходного возмущения имеют согласующиеся цели, которые могут быть достигнуты посредством обеспечения малости коэффициента усиления оператора выходной чувствительности.

3.5. Подавление шума

К сожалению имеются жесткие противоречия при выборе $\overline{\sigma } \left(S_o\right) \ll 1$, поэтому способ синтеза регулятора должен включать достижение некоторого компромисса. Первое противоречие касается подавления шума датчиков. Из (10) и схемы рис. 1 ясно, что поскольку после сумматора сигналы r и n становятся неразличимы, то хорошее слежение за задающим воздействием r приводит также к хорошему слежению и за шумом n. Действительно, выходная компонента сигнала, вызванная шумом, определяется так yn = – Tn. Тогда для подавления шума отношение

$\frac{{\displaystyle {||y_n\left(j\omega \right)||}_2}}{{\displaystyle {||n\left(j\omega \right)||}_2}} \le \overline{\sigma } \left[T_o\left(j\omega \right)\right].$

должно быть мало, что приводит к малости коэффициента усиления разомкнутой системы $\overline{\sigma } \left(L_o\right) \ll 1$, т.к. To = (I + Lo)–1 . Таким образом, для подавления выходного возмущения и шума должны одновременно быть малыми So и To, что невозможно из-за тождества To + So = I. Это противоречие между целями слежения (или подавления выходного возмущения) и подавления влияния шума разрешается посредством частотного разделения.

На низкой частоте, когда важно слежение, а шум датчиков мал, приемлем большой коэффициент усиления разомкнутого контура, который приводит к хорошему слежению и подавлению низкочастотного возмущения.

С другой стороны, на высоких частотах может доминировать шум над спектром полезного сигнала, и поэтому шум здесь должен быть подавлен. Более того, хорошее слежение на высоких частотах может привести к неприемлемым управляющим воздействиям, вызывающим насыщение исполнительных устройств, поэтому в этом случае требуется низкий коэффициент усиления разомкнутого контура.

3.6. Робастность

Второе противоречие связано с выбором функции чувствительности низкого уровня по отношению к робастности замкнутой системы.

Пусть P есть заданная номинальная модель объекта, чьей «верной» передаточной функцией является Pt. Предположим, что Pt располагается «по соседству» от P, что можно описать выходной мультипликативной неопределенностью вида

(15) $P_t=(I+\mathrm{\Delta })P.$

Для этого типа непараметрической (неструктурированной) ошибки модели, величина $\overline{\sigma } \left[\mathrm{\Delta }\right(j\omega \left)\right]$ обычно выбирается как возрастающая функция частоты ω. Для того, чтобы достигнуть хороших робастных запасов устойчивости, размер $\overline{\sigma } \left[\mathrm{\Delta }\right(j\omega \left)\right]$ величины ошибки моделирования $\mathrm{\Delta }$, которая входит в (15) без дестабилизации номинально устойчивой замкнутой системы, должна быть как можно больше. Если регулятор внутренне стабилизирует номинальный объект P, и как Р, так и Рt имеют одно и то же количество полюсов в ${\overline{C}}_{+}$, то размер наименьшей неопределенности $\mathrm{\Delta }$, для которой система становится неустойчивой, есть [8, 9, 11]

$\overline{\sigma } \left[\mathrm{\Delta }\right(j\omega \left)\right]=\frac{1}{\overline{\sigma } \left[T_o\right(j\omega \left)\right]}.$

Этот результат можно также трактовать с точки зрения теоремы о малом коэффициенте усиления для конфигурации $T_o-\mathrm{\Delta }$.

Теорема (о малом коэффициенте усиления – Small Gain Theorem) [1, 13]. Пусть $T_o\left(s\right)\in R{H}_{\infty }$ и $\gamma >0$. Тогда конфигурация с обратной связью $T_o-\mathrm{\Delta }$ корректна и внутренне устойчива для всех $\mathrm{\Delta }s\in R{H}_{\infty }$ и

${||\mathrm{\Delta }s||}_{\infty }\le \frac{1}{\gamma }\iff {||T_o\left(s\right)||}_{\infty }<\gamma .$

Таким образом, чем больше $\overline{\sigma } \left[T_o\right(j\omega \left)\right]$, тем меньше размер наименьшей дестабилизирующей неопределенности, следовательно, хорошая робастная устойчивость требует малого коэффициента усиления разомкнутого контура Lo, в частности, на высоких частотах, где модель объекта наименее надежна.