Цель обработки – повышение отношения сигнал/помеха. Все эти процедуры иногда называют общим словом – фильтрация, т.е. выделение чего-то из смеси с чем-то другим. Но чаще термин фильтрация относится к частотной фильтрации, т.е. разделению сигнал по частотному составу (спектру). Фильтры разделяются на одноканальные и многоканальные. Но многоканальные фильтры, как пространственные фильтры, имеют большое разнообразие, и по принципу действия обычно имеют собственное название: накопление, суммирование, смешение, миграция, вычитание волн и т.д.
Одноканальные частотные фильтры широко применялись и применяются в электротехнике и радиотехнике, имеют общее название электрических или аналоговых фильтров, так как содержат такие элементы, как электрические емкости, сопротивления и индуктивности. Такие фильтры еще называют физически реализуемыми или фильтрами реального времени, так как фильтрация в них осуществляется в процессе прохождения сигнала через эти цепи.
Цифровые фильтры, в отличие от аналоговых фильтров, имеют дело не с самим сигналом, а с его оцифрованным образом, и работают уже не в реальном времени, как бы быстро вычисление не производилось. Поэтому цифровые фильтры могут, как имитировать работу аналоговых фильтров, но также могут осуществлять те операции, которые в аналоговых фильтрах не могут быть реализованы по законам физики.
Частотная фильтрация сигналов
Если частотные спектры сигнала и помехи различаются, то с применением частотных фильтров можно добиться существенного повышения отношения сигнал/помеха (Бат М., 1980, Хаттон Л. и др., 1989, Харкевич А.А., 1962).
Частотные фильтры различаются по типу: фильтры высоких частот (ФВЧ) – пропускают высокие частоты и задерживают низкие (рис.2.1,a), фильтры низких частот (ФНЧ) – пропускают низкие частоты, задерживают высокие (рис.2.1,b), полосовые фильтры (ПФ) – пропускают сигналы внутри определенного интервала частот, за приделами этого интервала задерживают (рис.2.1,c), режекторные фильтры (РФ) – пропускают все частоты за исключением сигналов в узкой полосе частот вокруг заданной частоты (рис.2.1,d).
Кроме типа фильтра нужно еще указать, в каком частотном диапазоне работает данный фильтр. Для этого вводят понятие граничной частоты (или частот) фильтра. Обычно граничная частота фильтра определяется как частота, на которой коэффициент передачи фильтра падает до 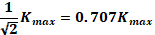 , где
, где  – коэффициент фильтра в полосе пропускания (рис.2.1).
– коэффициент фильтра в полосе пропускания (рис.2.1).
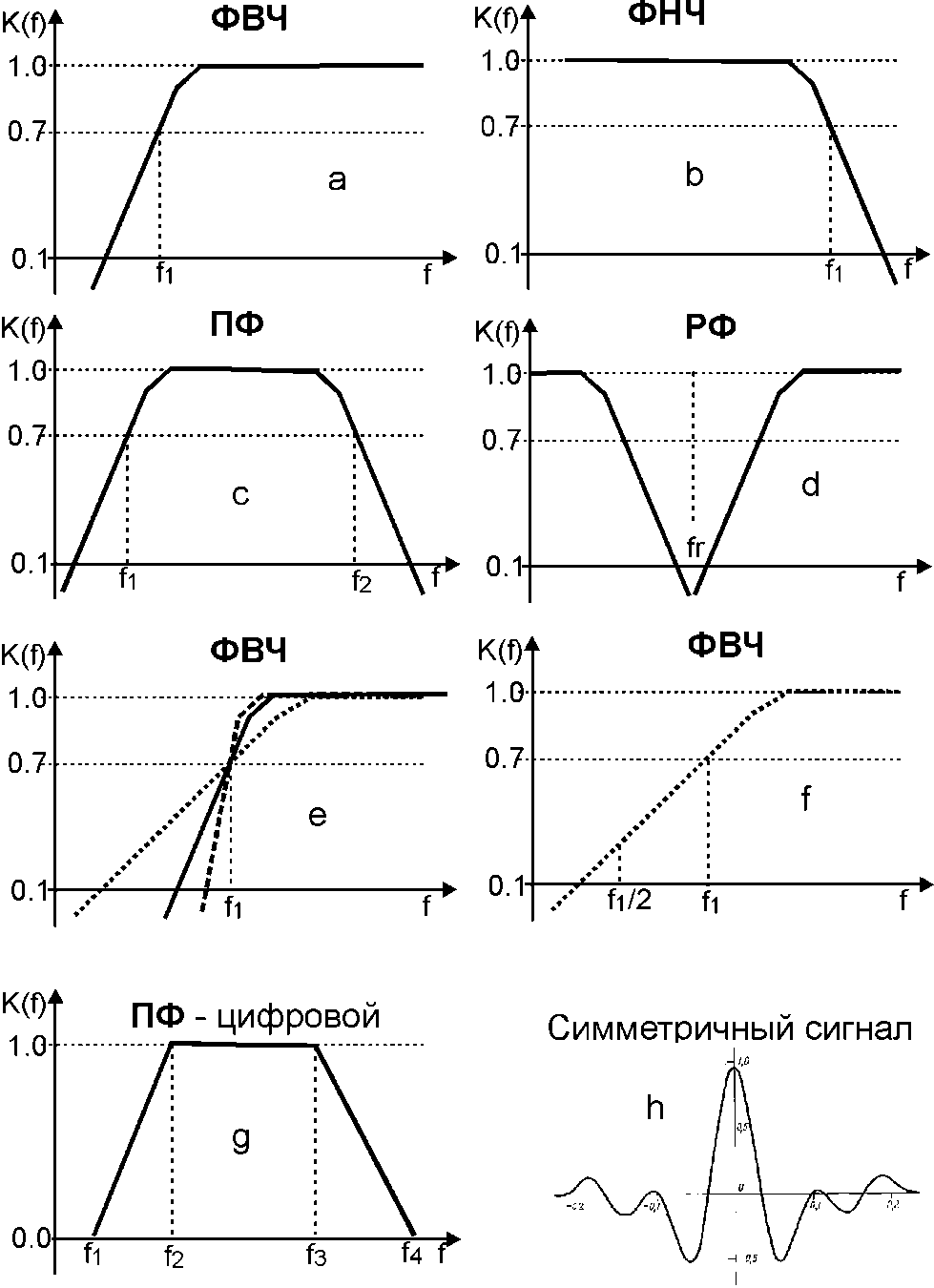
Рис. 2.1. Характеристики частотных фильтров: a) ФВЧ; b) ФНЧ; c) ПФ; d) РФ; e) фильтры с разной крутизной спада; f) определение крутизны спада характеристики фильтра; g) характеристика цифрового фильтра в виде трапеции; h) симметричный нуль-фазовый сигнал
Но фильтры одного и того же типа с одинаковой граничной частотой еще могут различаться крутизной склонов частотной характеристики (рис.2.1,e), который в радиоэлектронике принято измерять в дицебеллах на октаву (дб/окт). Октава – изменение частоты в два раза (рис. 2.1,f), а дицебелл – десятая доля Белла – единицы измерения энергии сигнала, которая пропорциональна квадрату амплитуды
D = log10E = log10A2 = 2 log10A.
Отсюда крутизна в дб/окт 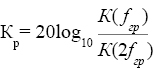 .
.
Перечисленные фильтры могут быть реализованы как электрические фильтры, выполняющие фильтрацию в реальном времени, а также в цифровом виде, когда фильтрация осуществляется вычислениями в компьютере уже зарегистрированных цифровых сигналов. Для характеристик электрических фильтров действуют определенные ограничения, связанные с принципом причинности. Например, их крутизны не могут быть бесконечно большими, фазовая и амплитудная характеристики определенным образом взаимосвязаны. Известны также другие недостатки аналоговых электрических фильтров: ограниченный динамический диапазон и нелинейные искажения, собственные шумы. Кроме того, в любой аппаратуре имеется только ограниченный набор фильтров, который не всегда позволяет подобрать оптимальные параметры фильтра.
Для цифровых фильтров многие эти ограничения не актуальны, так как вычисления производятся уже с оцифрованными данными, хотя существуют свои ограничения, связанные с особенностями вычислений. Цифровая фильтрация может осуществляться в области частот, простым вырезанием от спектра сигнала определенных частотных составляющих. Параметры такого фильтра принято задавать 4 частотами – фильтр с амплитудной частотной характеристикой в виде трапеции (рис.2.1, g). При этом фазовая характеристика фильтра может быть задана равной нулю (нуль-фазовый фильтр). Временной отклик такого фильтра будет симметричным относительно максимума (рис. 2.1, h). Конечно, такой фильтр не относится к физически реализуемым фильтрам, но симметричный сигнал на выходе фильтра оказывается удобным для корреляции границ на временных разрезах и может обеспечить максимальную разрешающую способность.
В цифровом виде могут быть реализованы и более сложные фильтры, почти в точности учитывающие характеристики спектра сигнала. Например, согласованный фильтр, когда амплитудная характеристика фильтра повторяет частотный спектр сигнала, чтобы еще более усилить эти частоты, или обратный фильтр, когда наоборот, амплитудная и фазовая характеристика фильтра выбираются обратными спектру сигнала, так что на выходе фильтра амплитудный спектр оказывается равномерной для всех частот, а фаза равна нулю. Это приводит к сжатию сигнала, и повышению разрешающей способности.
Согласно теории информации ширина спектра сигнала и эффективная длительность самого сигнала связаны обратно пропорциональной зависимостью, т.е. чем короче сигнал, тем шире его спектр, и наоборот, чем уже спектр, тем длиннее сигнал. Иными словами, справедливо соотношение неопределенности относительно сигнала и его спектра Δτ ∙ Δf  1–3.
1–3.
Это накладывает жесткие ограничения на возможности частотной фильтрации – для максимального повышения отношения сигнал/помеха часто нужно бы применить очень узкополосную фильтрацию, но это приведет к сильному растяжению сигнала и потере разрешающей способности. Для повышения разрешающей способности, наоборот, нужно бы максимально расширить спектр сигнала, но это может привести к резкому возрастанию уровня помех, и сделать сигнал невидимым. Поэтому на практике нужно выбирать оптимальную полосу частот фильтрации методом проб и ошибок.
Предсказывающая деконволюция
Из цифровых фильтров, которые не могут быть реализованы в аналоговом виде, наиболее часто используется предсказывающая деконволюция. Фильтр основан на Винеровской теории фильтрации по минимуму среднеквадратического отклонения. Согласно этой теории по сейсмической трассе предсказывается форма одиночного сигнала, затем оператор фильтра от каждого вступления сигнала в трассе вычитает предсказанную хвостовую часть, оставляя некоторую начальную часть сигнала, тем самым сокращая длительность сигнала и повышая разрешающую способность записи.
Алгоритм работы фильтра требует задания нескольких параметров, в частности, длины оператора, т.е. окна предсказания, и длины пропускаемой начальной части сигнала. Еще задается коэффициент «белого шума», который определяет устойчивость работы фильтра, т.е. чем меньше этот коэффициент, тем «жестче» работает фильтр, максимально сжимая сигнал, но соответственно повышается уровень шума на выходе фильтра.
Регулировка амплитуд
Амплитуда сейсмических волн уменьшается с расстоянием, а значит и со временем регистрации, по целому ряду причин.
Во-первых, это сферическое расхождение фронта волны. Так как размеры источника небольшие, он может считаться точечным на удалении. По этой причине амплитуда волны падает с расстоянием обратно пропорционально расстоянию (времени регистрации), т.е. 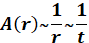 .
.
Другая причина спада амплитуд с расстоянием – поглощение энергии волн за счет неидеальной упругости среды. Амплитуда волн падает также за счет рассеяния на неоднородностях, малых по сравнению с длиной волны, а также при прохождении промежуточных границ. В среднем, такой спад амплитуд может быть описан экспоненциальным множителем.
Суммарный эффект от всех этих факторов может привести к изменению амплитуд сигналов вдоль трассы в сотни и тысячи раз. Естественно, при постоянном коэффициенте усиления вдоль трассы только какая-то часть сигналов может быть нормально видимой, остальные окажутся или слишком малой амплитуды, чтобы быть видимыми, или будут искажены до неузнаваемости. Поэтому требуется регулировка усиления сигналов вдоль сейсмической трассы.
Для компенсации сферического расхождения можно умножать амплитуды на коэффициент, обратно пропорциональный времени регистрации, т.е. k = α*t.
Для компенсации поглощения и рассеяния можно умножать их на экспоненциальный коэффициент, т.е. k = ebt .
Эта регулировка осуществляется по определенному одинаковому закону для всех трасс, поэтому еще называется программной регулировкой усиления (ПРУ).
Однако это очень обобщенные законы. На амплитуды сигналов сильно влияют также характер сейсмогеологического разреза, расположение приемников относительно источника, тип источника (взрыв в скважине, удар по поверхности, вибратор).
Если требуется более глубокая регулировка амплитуд вдоль сейсмических трасс, если необходимо, чтобы амплитуды сигналов были как можно более одинаковыми (например, для целей суммирования), то используется автоматическая регулировка усиления (АРУ). Такая программа вычисляет средний уровень сигнала в некотором интервале трассы и делит амплитуду сигнала на коэффициент, пропорциональный этому среднему уровню, так, что средний уровень сигнала по всем окнам вдоль трассы становится одинаковым. Однако сами коэффициенты не запоминаются, и это приводит к потере информации об относительных амплитудах сигналов.
Последовательность выполнения задачи
Для последующей обработки данных создадим новый поток, назовем ее, к примеру, 20-Preprocessing. В данной задаче мы будем пытаться улучшить соотношение сигнал/помеха в наших данных, уже загруженных в базу системы. Поэтому считывать их будем процедурой Trace Input. Контролировать качество результатов можно, выводя данные на экран в виде временных разрезов, для пробы считывая данные только по одному каналу из всех сейсмограмм, или рассматривая многоканальные сейсмограммы, тогда для быстроты считывая только определенную часть сейсмограмм. После выбора всех параметров обработки, следует в процедуре ввода указать все сейсмограммы и все каналы, а обработанные данные сохранить процедурой Trace Output, как новая база данных (например: file_preproc).
Меню процедуры Trace Input выглядит так (рис. 2.1).
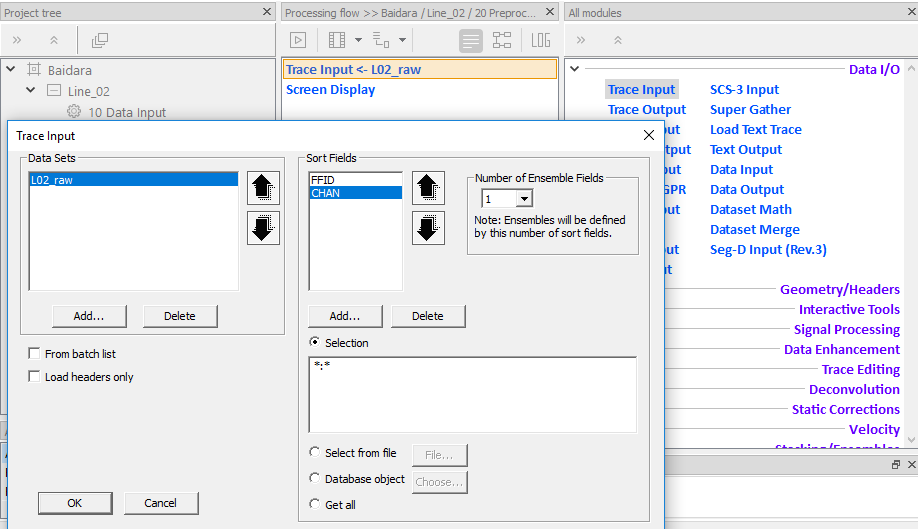
Рис. 2.1. Меню процедуры Trace Input
В появившемся меню процедуры (рис. 2.1) в окно Data Sets нужно вставить имя базы данных, откуда теперь будем считывать данные. Для этого нужно кликнуть по кнопке Add и в появившемся внутреннем директории RadExPro выбрать нужный файл.
Затем в окно Sort Fields нужно вставить поля заголовков трасс, по которым будет осуществляться сортировка трасс при вводе. В начале рекомендуется поставить те же поля заголовков трасс, как и при вводе данных в первом потоке, т.е. FFID и CHAN.
Второй процедурой следует поставить Screen Display, теми же параметрами, что и в первом потоке. Кстати, можно второй поток заново не создавать, а просто создать копию первого потока, изменить название потока, затем стереть там все процедуры, кроме Screen Display, а потом спереди поставить Trace Input.
В случае, если хотим данные наблюдать в виде временного разреза, то сортировать их следует сначала по номерам полевой записи – FFID, затем CHAN, сортируя трассы с каждого пункта возбуждения в порядке их полевой записи. В окно Selection вставляем сначала звездочку (*), что означает считать все сейсмограммы, или указываем диапазон считываемых сейсмограмм. После звездочки ставим разделитель – двоеточие (:), после него – номер трассы, который с каждой сейсмограммы надо считывать (более подробно о задании выбора трасс в этом окне читайте в прилагаемом описании процедуры).
Если данные надо наблюдать как многоканальные сейсмограммы, то во второе поле можно поставить звездочку (все каналы), или указать, с какого по какой канал нужно считать.
Второй процедурой в этом потоке поставим Screen Display, настройки ее скопируем с первого потока – 10-Data Input.
Теперь запустив этот поток (20-Preprocessing) убедимся, что сохраненные в базе данных записи полевого файла читаются, и получается такое же изображение временного разреза, как и в первом потоке (рис. 1.5), или многоканальные сейсмограммы (рис. 1.10).
Далее приступаем к применению частотной фильтрации. Для выбора параметров фильтра сначала определим частотные спектры сигнала и помехи. Для этого воспользуемся инструментом расчета спектров в модуле Screen Display. После того, как поток (рис. 2.1) выдаст изображение сейсмограмм на экране (рис. 2.2), следует кликнуть на главном меню последовательность кнопок Tools->Spectrum->Average, затем переместить маркер на изображение сейсмограмм, и выделить прямоугольник на желаемом месте изображения, скажем, для вычисления спектра сигнала там, где сигнал лучше виден (синий прямоугольник на рис. 2.2). Осредненный спектр сигналов, попадающих в этот прямоугольник, появится в соответствующем окошке спектров (рис. 2.2, зеленый спектр). Точно также можно вычислить спектр помех (рис. 2.2, оранжевый прямоугольник и оранжевый спектр).
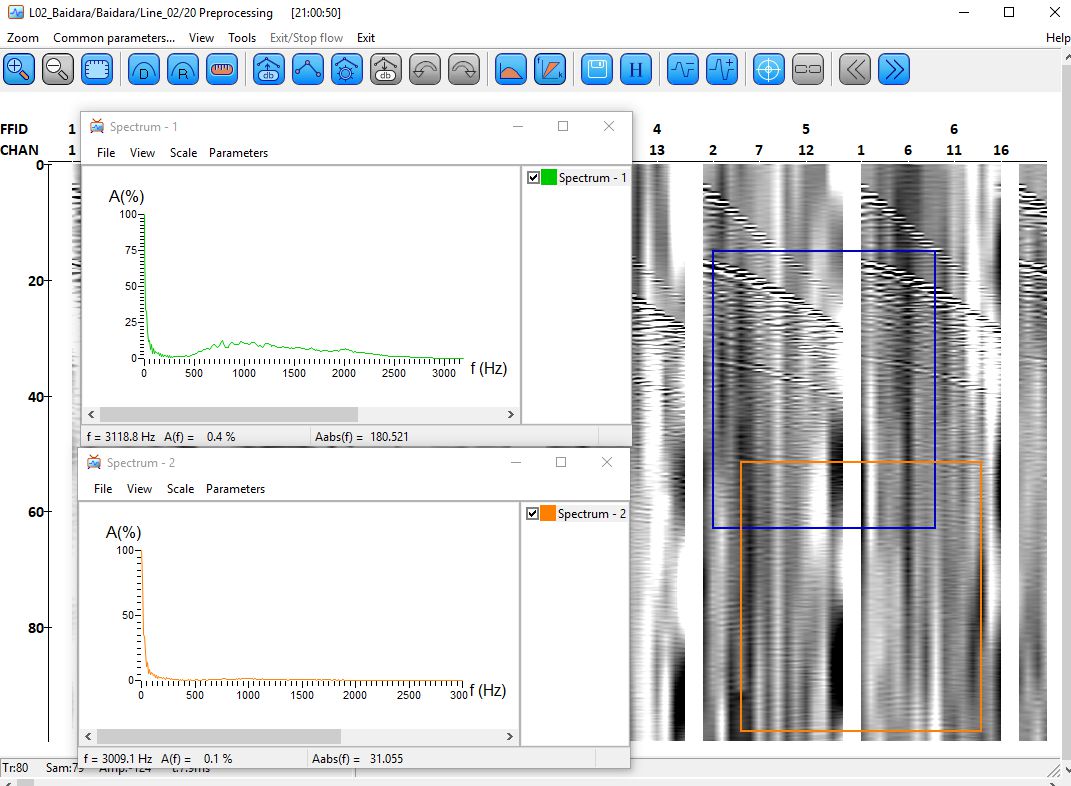
Рис. 2.2. Расчет спектров сигнала и помехи
Так как сигнал (в синем прямоугольнике) записан вместе с помехой, то в спектре этого интервала записи (зеленая кривая) присутствуют как относительно высокочастотные составляющие сигнала (интервал частот 500–2500 Гц), так и резко выраженные низкочастотные составляющие помехи (интервал частот 0–100 Гц). Это хорошо подтверждается спектром, вычисленном в оранжевом окне, где сигнал становится практически незаметным – здесь в спектре преобладают низкочастотные составляющие (ниже 100 Гц), а частоты, соответствующие спектру сигнала (500–2500 Гц) пренебрежимо малой амплитуды.
Для избавления сигнала от вышеуказанной помехи в поток вставим процедуру полосовой частотной фильтрации Bandpass Filtering с частотами среза 50, 100, 2000, 3000 Гц (рис. 2.3). Для визуальной оценки результатов фильтрации после этой процедуры вставим еще один модуль Screen Display, продублировав первый такой модуль в потоке.
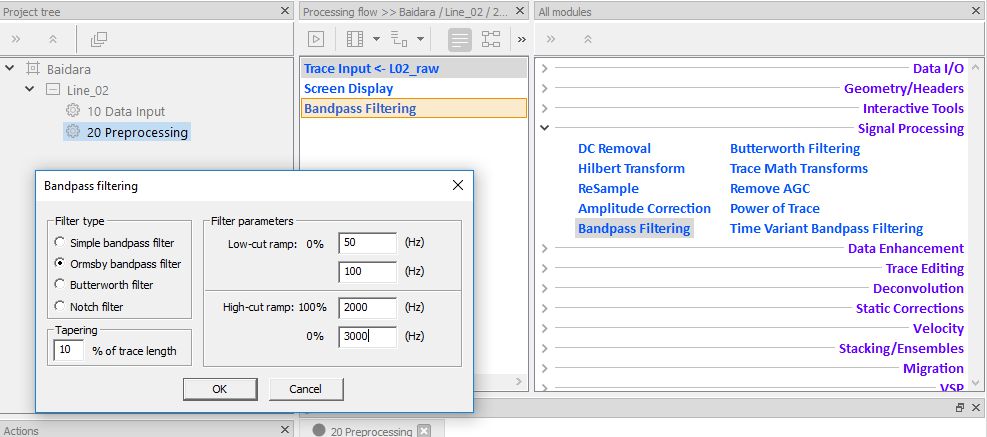
Рис. 2.3. Настройка параметров процедуры Bandpass Filtering
Запустив поток, сначала увидим исходные данные, не отфильтрованные (рис. 1.10). Выйдя из этого изображения (Exit), продолжим работу потока, а именно, проработает процедура Bandpass Filtering, затем второй модуль Screen Display выдаст изображение уже отфильтрованных данных (рис. 2.4).

Рис. 2.4. Отфильтрованные сейсмограммы
Аналогично реализуются и другие способы предварительной обработки данных, такие, как различные способы регулировки амплитуд, деконволюция, редактирование трасс.
Процедуры деконволюции и регулировки амплитуд рассмотрим на примере файла одноканальных данных SFilan15 (Рис.2.5)
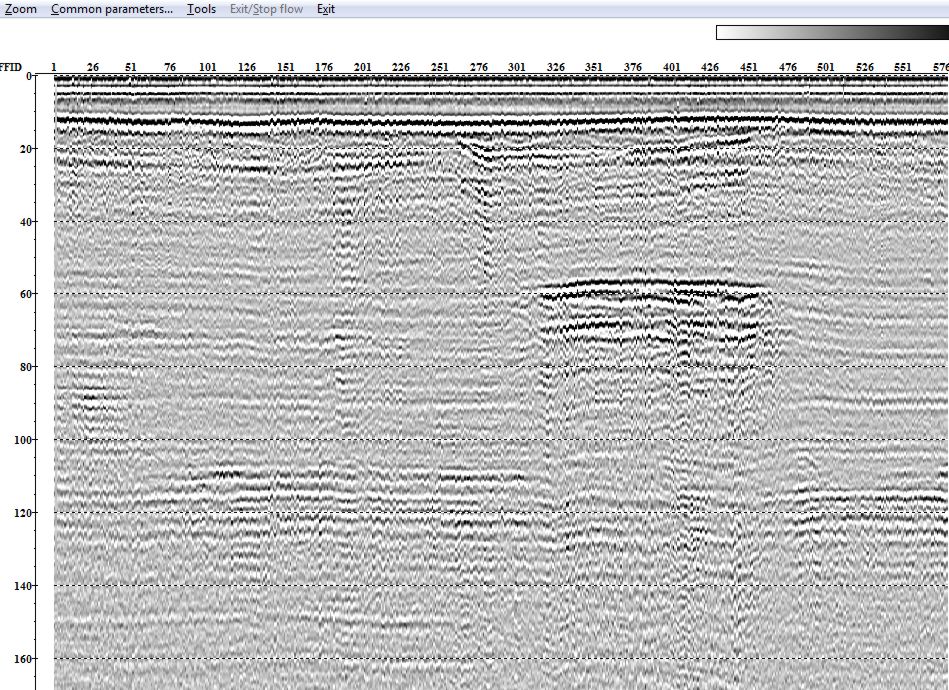
Рис. 2.5. Временной разрез SFilan15 после фильтрации
Если внимательно присмотреться к временному разрезу на рис.2.5, то можно заметить, что почти каждая граница сопровождается некоторым повтором самой себя с интервалом времени, равным примерно 10 мс. Это многократные волны или волны-спутники. Для борьбы с этим явлением попробуем применить процедуру Predictive Deconvolution (рис. 2.6).
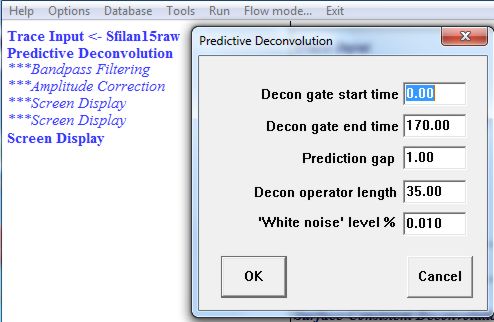
Рис. 2.6. Меню процедуры Predictive Deconvolution
Во всплывшем меню процедуры устанавливаем параметры, исходя из длительности повторных импульсов и желаемой длительности самого сигнала. В нашем примере мы выбрали интервал действия процедуры почти на всю длину трассы (0–170 мс), желаемую длину сигнала 1 мс, а длину всего оператора, т.е. интервал времени, на котором будут подавляться повторные колебания сигнала, – 35 мс. Уровень белого шума оставили таким, как первоначально было задано в программе – 0.01. Для первоначальной настройки процедуры все остальные процедуры обработки пока можно сделать неактивными (рис. 2.6).
Запустив поток, получаем временной разрез, на котором все повторяющиеся сигналы оказываются заметно ослабленными, но уровень шумов кажется более высоким. Это из-за того, что деконволюция пытается выровнять весь частотный спектр сигнала, и поднимает одновременно и те частоты, на которых преобладают помехи. Поэтому после деконволюции теперь полезно применить уже настроенный нами ранее полосовой частотный фильтр (рис. 2.7). Естественно, такой разрез легче интерпретировать, в нем почти нет ложных границ.

Рис. 2.7. Временной разрез SFilan15 после процедуры
Predictive Deconvolution и полосовой частотной фильтрации
Для дальнейшего улучшения качества временного разреза применим процедуру Amplitude Correction, для чего перетащим ее со списка процедур в левое окно и во всплывшем меню выберем для начала Spherical divergence correction – компенсацию сферического расхождения фронта волны (рис. 2.8). Эта регулировка умножает амплитуды сигнала на коэффициент, пропорциональный времени вступления сигнала. В результате амплитуды сигналов в начале записи уменьшаются, к концу – увеличиваются, что и можно увидеть после выполнения потока (рис. 2.9). Как улучшение можно считать, что яркие пятна в середине разреза (пикеты 320–460) на времени 60 мс стали лучше выделяться, а также отражения от более глубоких границ стали более интенсивными.
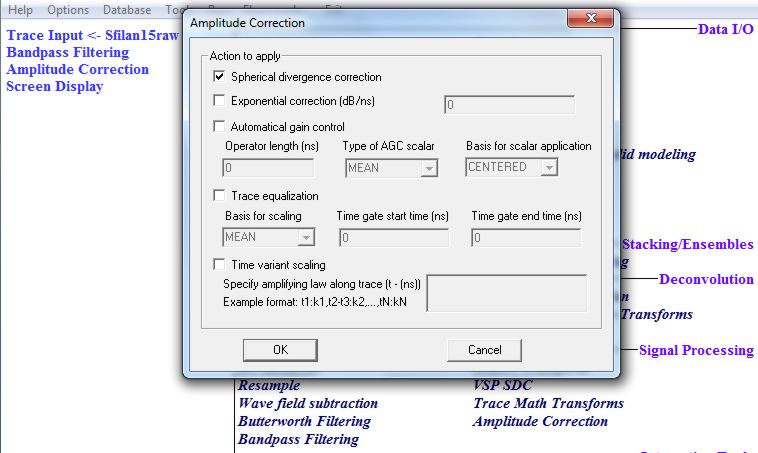
Рис. 2.8. Меню процедуры Amplitude Correction
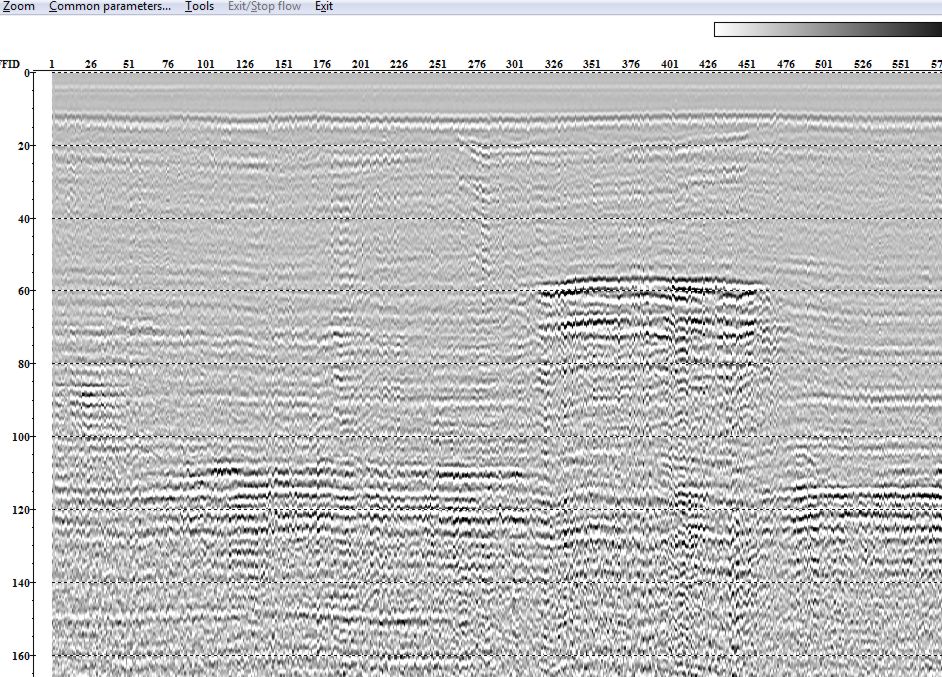
Рис. 2.9. Временной разрез SFilan15 после фильтрации
и компенсации сферического расхождения
В качестве второго примера можно попробовать применить автоматическую регулировку амплитуд Automatical gain control (рис. 2.10). Выберем длину оператора 20 мс, в качестве нормирующего множителя будем использовать среднее значение амплитуд в окне (MEAN), а регулировку будем применять к амплитудам в центре этого окна (CENTERED). Запустив поток с такой регулировкой амплитуд получаем временной разрез (рис. 2.11), на котором оси синфазности очень хорошо прослеживаются, но различия амплитуд сильных и слабых отражений сгладились.
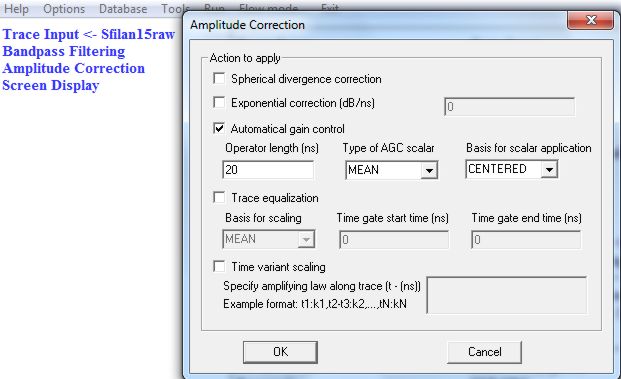
Рис. 2.10. Меню процедуры Amplitude Correction
с выбранными параметрами режима Automatical gain control
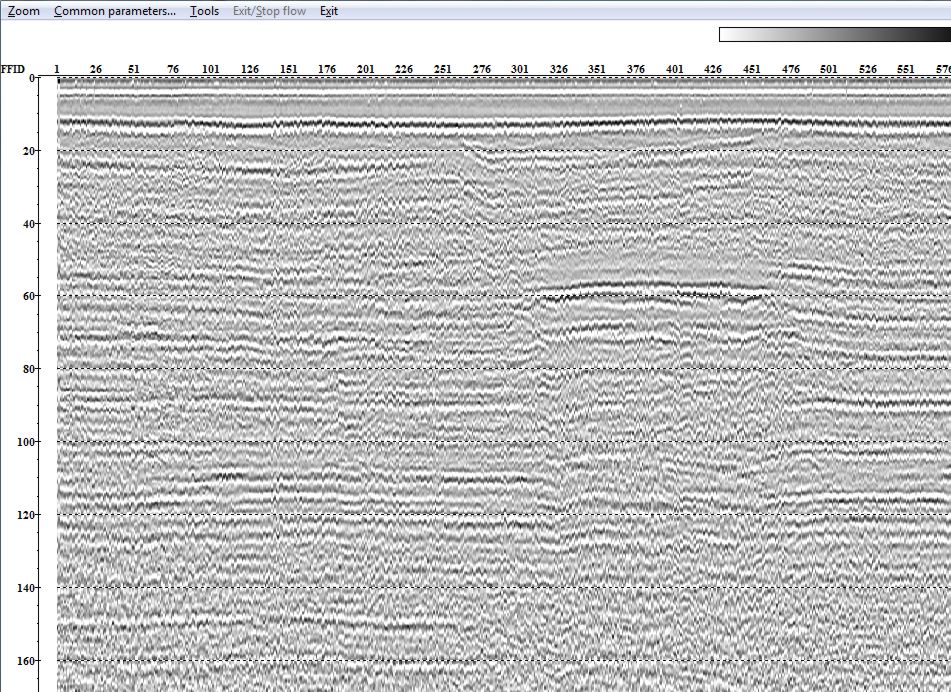
Рис. 2.11. Временной разрез после применения процедуры
Amplitude Correction в режиме Automatical gain control
Для самостоятельной обработки студентам даются файлы многоканальных сейсмоакустических данных. Необходимо к этим данным применить всю описанную последовательность процедур с выбором оптимальных параметров, так, чтобы после обработки разрез стал вполне читаемым, т.е. можно было проследить основные границы, и понять геологию.
Когда все процедуры с соответствующими параметрами выбраны, в процедуре Trace Input выбирается ввод данных всех каналов и всех нужных номеров сейсмограмм, в конце потока ставится процедура Trace Output, которая сохраняет обработанные трассы в базу данных, например, под названием L02_Preproc для дальнейшей обработки уже с многоканальными процедурами.

