Численное решение уравнений биокинетики в курсах «Общая экология» и «Моделирование биологических процессов»

Действительно, при разработке и совершенствовании методов интегрирования производится максимальное упрощение структуры уравнений (1). Для решения конкреных, особенно инженерно-прикладных задач нет необходимости использовать всю полную систему (1)–(3), т.к. с одной стороны, это сделало бы модель необозримой и не реализуемой 29, а с другой стороны, каждая конкретная экосистема допускает существенное упрощение модели трансформации вещества соответственно характеру поставленного вопроса. Чтобы облегчить выбор оптимальной модели и устранить произвол в процедуре упрощения, необходимы разработки типизации и схематизации условий [Айзатуллин и Лебедев, 1977, с. 30–31].

Очевидный путь упрощения системы уравнений (1) состоит в сокращении размерности пространственно-временной области, что будет выражаться в уменьшении числа независимых переменных. Пока рассматриваемая система задана в 4-мерной области: мы имеем три независимых переменных (х, у, z) по пространственным направлениям и еще одну независимую переменную – время t.

Одно из важнейших свойств открытых биологических систем – установление в них стационарных состояний в отличие от термодинамического равновесия, свойственного изолированным системам. По определению в стационарном состоянии все производные по времени обращаются в нуль. Отсюда, приравнивая нулю правые части [Рубин и др., 1987, с. 9] (1), получим систему (1.3.0) – см. рис. 1.

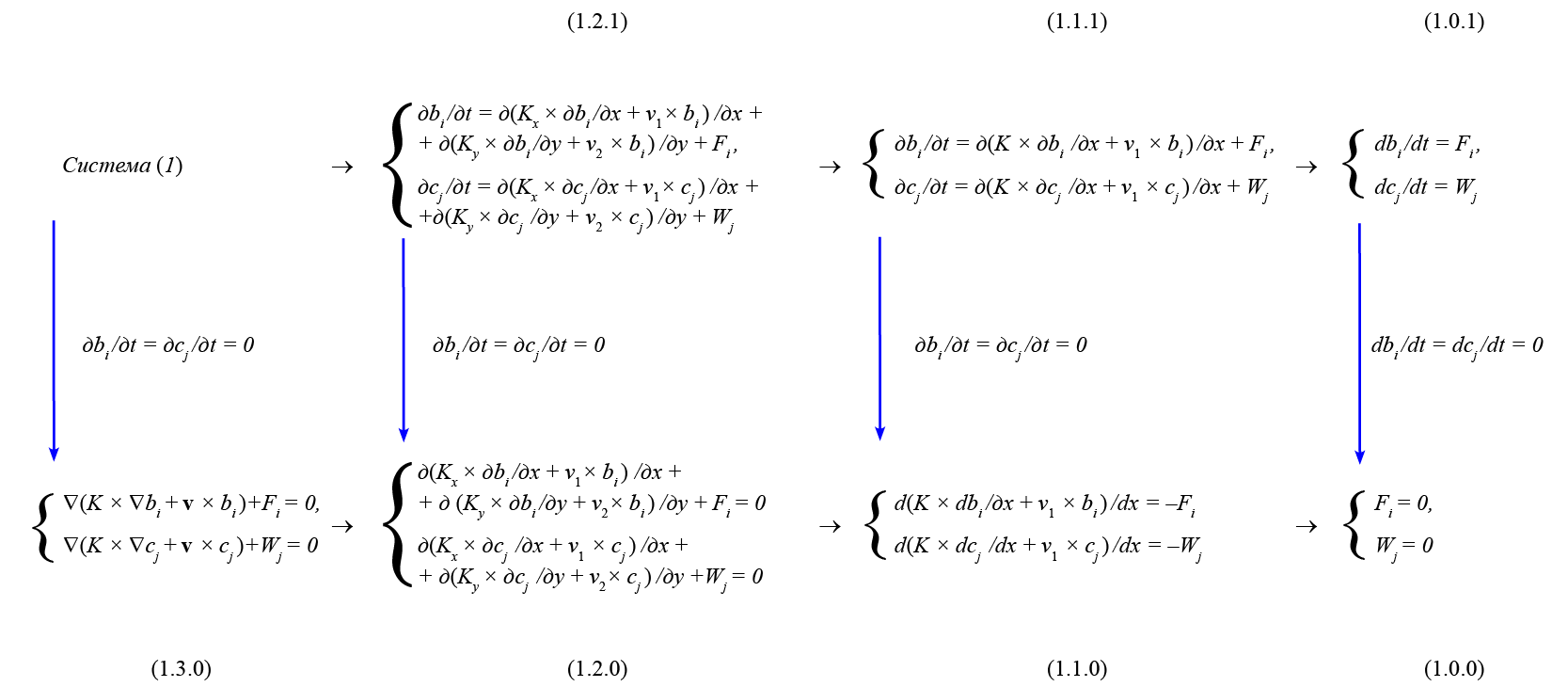
Рис. 1. Пути упрощения общей системы биологической кинетики.
Горизонтальные стрелки обозначают изъятие из рассматриваемой системы одного пространсвенного
измерения, например, при переходе от «системы (1)» к (1.2.1) и, аналогично,
от (1.3.0) к (1.2.0), из рассмотрения исключается координата z.

Однако вместо удаления производной по времени из модели (1), мы в некоторых ситуа-
циях могли бы выполнить аналогичное упрощение в пространсвенной области – удалить одну из пространственных координат (для определенности будем считать, что отбрасывается координата z). С формальной точки зрения это означает, что

д(Kz × дbi /дz + v2 × bi )/дz = д(Kz × дcj /дz + v2 × cj )/дz = 0,

а по физическому смыслу соответствует отсутствию 30 переноса вдоль оси z. При этом система (1) упрощается до (1.2.1) 31 – см. рис. 1.

Если окажется возможным удалить еще одну пространственную координату (для определенности будем считать, что отбрасывается координата y), то (1.2.1) упростится до (1.1.1) 32.

Посмотрим, какими величинами мы должны пренебречь, чтобы система (1.1.1) переходила в систему обыкновенных дифференциальных уравнений (1.0.1). Такая редукция возможна если внешние параметры можно считать постоянными во всем объеме Q, так же как и начальные условия. Таким образом, если внешние условия и начальные концентрации однородны во всем объеме Q, то достаточно рассматривать точечную систему. Другой случай, когда точечная система хорошо описывает кинетику, – случай больших коэффициентов диффузии. Если скорости диффузии велики по сравнению со скоростями процессов Fi  и Wj , то прежде чем существенно изменятся концентрации [Рубин и др., 1987, с. 75] bi  и cj , произойдет перемешивание во всем объеме и мы придем к рассмотренному выше случаю однородности во всем объеме Q.

Если для системы (1.1.1) мы будем рассмаривать стационарное состояние, то, полагая производные по времени равными нулю, придем к системе (1.1.0), которая, очевидно, содержит обыкновенные дифференциальные уравнения, как и система (1.0.1). Однако на рис. 1 мы привели только преобразования системы уравнений (1), но не затрагивали вопрос о дополнительных условиях (2) и (3). А ведь при тех или иных упрощениях (1) они тоже будут меняться соответствующим образом. Если отбрасываются производные по времени, то исчезнут начальные условия (3), ибо теперь в них нет никакого смысла – в стационарном состоянии значения bi  и cj  не меняются и определяются в любой момент времени из решения самой системы уравнений. А если отбрасывается какая-либо пространственная переменная, то исчезает необходимость ставить граничные условия (2) по этой переменной – раз в пространстве нет данного направления, то и нет границ на этом направлении.

В связи с только что сказанным, задачи (1.0.1) и (1.1.0) будут существенно различаться. Подчеркнем: именно задачи будут различаться, а тип системы уравнений в обоих случаях будет один и тот же – обыкновенные дифференциальные уравнения (ОДУ). Чем же тогда различаются задачи? Для системы (1.0.1) будут даны начальные условия (при том, что граничных условий не будет) и, следовательно, надо найти такие bi  и cj , которые при t = 0 удовлетворяют условиям (3).

Если решение системы ОДУ нужно определить в том случае, когда заданы все его компоненты в одной «начальной точке» (при каком-то значении независимой переменной, вообще говоря – не обязательно при нулевом), то это – задача с начальными условиями [Шампайн и др., 2009, с. 158] (ЗаСНУ) 33. А вот для системы (1.1.0) будут даны граничные условия (при том, что нет начальных условий).

Если значения компонент решения или определенные соотношения между ними задаются в нескольких точках (при соответствующих значениях независимой переменной, принадлежащих определенному интервалу), то это – задача с граничными условиями [Шампайн и др., 2009, с. 158] (ЗаСГУ) 34.

Наконец, приравнивая нулю правые части системы обыкновенных дифференциальных уравнений (1.0.1) [Рубин и др., 1987, с. 9], получим систему алгебраических или трансцендентных уравнений (1.0.0) 35 – см. рис. 1.

---