♦ La fonction dont (1) le graphe est représenté sur la fig. 1 admet six extremums locaux stricts dont (1) deux sont globaux.
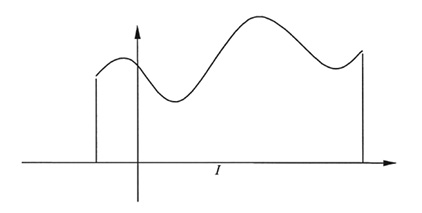
Figure 1: Extremums locaux
Si la fonction est dérivable, on a une condition nécessaire pour avoir un extremum local:
Soient f une fonction dérivable sur un intervalle ouvert I et x0 un point de I. Si f admet un extremum local en x0, alors f ‘ (x0) = 0.
◊ Attention, cette condition n’est pas suffisante: il se peut que la dérivée s’annule sans qu’il y ait (2) un extremum local. Par exemple, la fonction [x |→ x3], définie sur [–1, 1], n’admet pas d’extremum local en 0, bien que sa dérivée s’annule (3) en 0.
◊ Soit f une fonction définie sur [a, b]. Il est possible que f admette (4) un extremum en a ou b sans que f ′(a) ou f ′(b) soit (2) nul. Par exemple, la fonction f : x |→ x2 définie sur [0, 1] admet un maximum en 1, mais f ′(l) ≠ 0.
♦ La fonction [ x |→ x (l – x) ], définie sur [0, 1] admet un maximum global (strict) au point 1/2. On a donc l’inégalité
∀ x ∈ [0, 1], x (1–x ) ≤ 1/4
A l’aide de cette condition nécessaire, on démontre le résultat suivant:
Théorème de Rolle. Soit f une fonction définie sur un segment [a, b] (avec a < b), dérivable sur l’intervalle ouvert ]a, b[, et telle que f (a) = f (b). Alors, il existe un élément c de ]a, b[ tel que f ′(c) = 0.
Vocabulaire:
|
extremum [εkstrεm⊃m] (m) |
экстремум |
|
local, -e |
локальный |
|
admettre qch. |
допускать; обладать, иметь; принимать |
|
strict [strikt], -e |
строгий, точный |
|
global, -e |
глобальный |
|
il se peut |
может случиться |
|
s’annuler |
обращаться в ноль |
|
sans que |
без того, чтобы |
|
bien que |
хотя |
|
maximum [maksim⊃m] (m) |
максимум |
|
inégalité (f) |
неравенство |
|
aide (f), |
помощь |
|
à l’aide de qch |
при помощи ч.-л. |
|
démontrer qch |
доказать что-л. |
|
résultat (m) |
результат |
|
suivant, -e |
следующий, -ая |
|
théorème (m) |
теорема |
|
segment (m) |
отрезок; сегмент |
Lecture de formules et de symboles:
|
fig |
figure |
|
х3 |
х cube, х puissance 3 |
|
[a, b] |
intervalle fermé a b ou segment a b |
|
]a,b[ |
intervalle ouvert a b |
|
f : x |→ x2 |
f transforme x en x carré |
Des éléments de grammaire de texte:
Des articulateurs et des substituts:
a) soient, soit, alors, attention, par exemple, donc, si;
b) dont, cette (condition) sa (dérivée), telle que, tel que.
Structurer:
– Attention au symbole graphique du texte ||, mettant en relief des idées – clés. (Обратите внимание на графический знак текста ||, выделяющий основные мысли).
– Attention aux sous – titres, aidant à grouper l’information (Обратите внимание на подзаголовки, помогающие сгруппировать информацию): Figure 1: Extremums locaux; Théorème de Rolle.
– N.B. Dans le discours oral les idées – clés seront mises en relief par des articulateurs: définissons... (donnons la définition), d’après le théorème..., ce dessin représente... etc.
Révision de la grammaire de base:
(1) Dont – относительное местоимение (pronom relatif).39
(2) (3) Союзы “sans que” и “bien que” требуют после себя употребления сослагательного наклонения (Subjonctif).40
(4) Сослагательное наклонение (Subjonctif).41

