Рассматривается произвольная трехмерная область Q (ограниченная поверхностями Гk , k = 1,… s), для которой определяется система декартовых координат, и с помощью полуэмпирического уравнения турбулентной диффузии совместно описываются массоперенос и трансформация живого и косного вещества с учетом распределения освещенности и температуры:
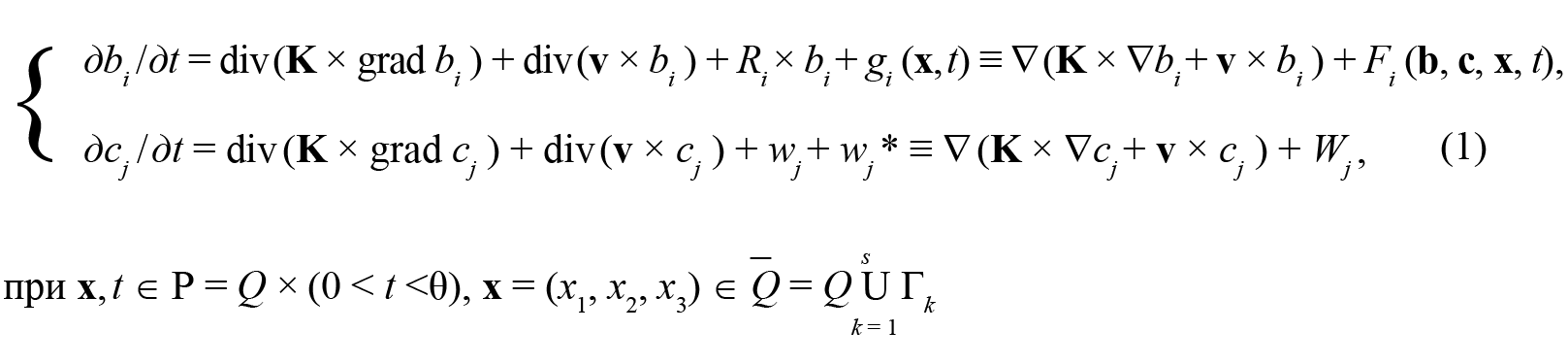
где bi – концентрации организмов и детрита (i = 1,… m); cj – концентрации веществ (j = 1,… n); x – точка с координатами x1 = х, x2 = у, x3 = z 10; v – вектор скорости течения с проекциями vα (α = 1, 2, 3); K – коэффициент турбулентной диффузии 11. Члены Ri (b, c, I, T, K) × bi описывают скорости трансформации живого и косного взвешенного вещества; wj *(b, c, I, T, K) – скорости гетерогенной физической (адсорбция), химической и биохимической трансформации веществ; wj (b, c, I, T, K) – то же, но протекающей гомогенно; div(K × grad bi ) и div(K × grad cj ) – турбулентная диффузия 12 компонентов; div(v × bi ) и div(v × cj ) – адвективный массоперенос 13; gi (x, t) – скорость дополнительного массопереноса, включая седиментацию и миграции [Айзатуллин и Лебедев, 1977, с. 29–30]. Здесь T = T(x, t) и I = I(b, x, t) – функции, задающие, соответственно, температуру и освещенность. Для простоты записи мы ввели Fi (b, c, x, t) = Ri × bi + gi (x, t) и Wj = wj + wj *, а также использовали оператор Гамильтона (набла-оператор), который в декартовых координатах имеет вид: ∇ = (д/дх) × i + (д/дy) × j + (д/дz) × k, где i, j, k – попарно перпендикулярные друг другу единичные векторы, задающие декартову систему координат.
Кроме того, ставятся дополнительные условия: граничные

где Âik и Ĉjk – операторы граничных условий, а φik (x, t) и ψjk (x, t) – граничные функции, содержание которых назначается, исходя из специфики задачи [Айзатуллин и Лебедев, 1977, с. 29–30]; Bi (x) и Cj (x) – функции, задающие начальное (т.е. в начальный момент времени) распределение переменных bi и сj по пространству x.
Задача в такой общей постановке, возможно, не слишком наглядна. Поэтому рассмот-
рим ряд примеров.
10 Ось х3 обычно направляется вертикально вниз [Айзатуллин и Лебедев, 1977, с. 29] если моделируется водоем или почва и вверх – если атмосфера.
11 По-видимому, Айзатуллин и Лебедев [1977, с. 29] принимали, что коэффициент турбуленной диффузии представляет собой одно скалярное значение. Однако, поскольку коэффициенты турбулентной диффузии вдоль различных направлений могут существенно различаться (как это имеет место, например, в приземном слое атмосферы, где вертикальный коэффициент диффузии значительно меньше горизонтального [Калиткин и др., 2005, с. 17–19]), то для большей общности принято рассматривать вектор К с компоненами К1, К2 и К3 – см., например, [Дружинин и Шишкин, 1989, с. 61]. Если говорить о диффузии молекулярной, а не турбулентной, то все равно мы не можем ограничиться одним значением, поскольку коэффициенты диффузии могут различаться для разных компонент bi и сi (например, при 20 °С коэффициенты диффузии рафинозы и щавелевой кислоты в водном растворе составляют, соответственно, 0.36 × 10–5 и 1.53 × 10–5 см2/с [Елецкий, 1991, c. 380]). Для самых «продвинутых» читателей заметим: на еще более высоком уровне строгости оказывается, что коэффициенты турбулентной диффузии наиболее правильно задавать тензором – см., например, [Галкин и Корнейчук, 1981]; но в такие дебри мы здесь залезать не будем.
12 Если говорить более строго, то это – «скорость турбуленной диффузии».
13 Если говорить более строго, то это – «скорость адвективного массопереноса». Впрочем, нет предела совершенству – можно взойти на еще более высокий уровень срогости. Например, в усложненных моделях типа хищник-жертва К.Э. Плохотникова [2017, с. 57] (в которых предполагается преследование хищником своей жертвы и, наоборот, убегание жертвы) член div(v × bi) описывает как раз это активное движение, причем тогда v = λi × grad(bm), где m ≠ i. Т.е. в уравнении, описывающем динамику популяции жертвы, v зависит от концентрации хищника, а в уравнении динамики популяции хищника, v зависит от концентрации жертвы (таким образом, поскольку v для жертвыи и хищника – разные, то следует записывать их с соответствующим индексом: vi). Но если нет макроскопического движения среды, а есть лишь движние отдельных элементов, то разве можно назвать это «адвективным массопереносом»? Кстати, в еще более общем случае – когда и сама среда может двигаться, и организмы внутри нее могут активно перемещаться (например: хищники и жертвы в реке), v = λi × grad(bm)+vо, где vо – вектор скорости перемещения (течения) среды.

