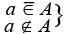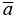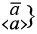Французский язык для математиков

=

égal à...

≠

différent de...

>

supérieur à...

<

inférieur à...

≥

supérieur ou égal à...

au moins égal à...

≤

inférieur ou égal à...

au plus égal à...

≡

égal identiquement à...

correspond à...

≈

égal environ à...

peu différent de...

asymptotiquement égal à...

$\nearrow$

croit

$\searrow$

décroît

→

tend vers…

∞

infini

a ∝ b

a égal b à une constante près

( )

parenthèses

[ ]

crochets

{ }

accolades

" "

guillemets

+

plus

–

moins

±

plus ou moins

+

moins ou plus

x или ·

signe de multiplication (multiplié par)

:

signe de division (divisé par)

/ или –

barre de fraction

,

virgule

.

point

…

etc. (et cetera)

a ~ b

a est équivalent à b

º

degré

,

minute

"

seconde

∠

angle

d, D

angle droit

, ∠α

angle alpha

┴

perpendiculaire à...

a'

a prime

a1

a indice un

a*

a astérisque

a ∈ A

l’élément a appartient à l’ensemble A

l’élément a n’appartient pas à l’ensemble A

A ⊂ B

A est inclus dans B

a

a ondulé

a tiret (s’emploie pour indiquer le nombre conjugué d’un nombre complexe donné)

⇒

implique

a – b = 0 ⇒ a = b

du fait que a moins b égal zéro découle que a égal b

|a|

valeur absolue de a; module de a

a’1

a prime indice un

a’’1

a deux primes indice deux

am

a indice m

f (x)

f de x; fonction de x

D x

accroissement de x

∑

signe somme

an

a puissance n

valeur moyenne de a

n!

factorielle n

Pn

nombre de permutations de n objets (P indice n)

nombre d’arrangements de n objets p à p (A indices n, p)

nombre de combinaisons de n objets p à p (C indices n, p)

Pn = n!

permutation de n éléments

b

∑ x (n)

n=a

sigma, de n = a à n = b, de x (n)

%

pour cent

*

astérisque

∃

existence

∃ i

il existe un i tel que...

∀ i

pour tous les i tels que...

M

module du système de log. de base 10

par rapport au système de base e (M = log10e = 0.43429)

E(a)

partie entière de a

a = b

a égal b

a > b

a est supérieur à b; a est plus grand que b

a ≥ b

a est égal ou supérieur à b

a < b

a est inférieur à b; a est plus petit que b

a ≤ b

a est égal ou inférieur à b

a + b

a plus b

a – b

a moins b

ab

ab: a multiplié par b; produit ab

$\frac{a}{b}$

a sur b: a divisé par b

k

∑ ai

i=m

somme de m à k ;
somme des ai quand i va de m à к

∑ ai

i<n

somme des ai pour les indices i plus petits que n

∑ ai

i≠s

somme des a; pour les indices i non égaux à s

∞

∑ ai

i=k

somme des a; de k à l’infini

double somme des aij pour i allant de m à n et j de k à l

∞

∑ aij

i,j=k

double somme des aij, les indices i et j allant de к à l’infini

n

П ai

i = m

produit des a; pour i allant de m à n

∞

П ai

i = m

produit des ai pour i allant de m à l’infini

a2

a au carré; a carré

a3

a au cube; a cube

a± n

a à la puissance plus ou moins n

a à la puissance к sur n

√

racine carrée de...

3√

racine cubique de...

n√

racine n-ième de...

√ a

racine de a

3√ a

racine cubique de a

n√ a

racine n-ième de a

e x

e à la puissance x

exp x

exponentielle de x

exp [ f (x)]

exponentielle de f (x); exp f (x) = e f (x)

log

logarithme

log10

logarithme décimal

ln

logarithme naturel (népérien)

logb a

logarithme du nombre a avec la base b

logarithme du nombre a de base b

ln a

logarithme népérien de a

log x

log2 x}

logarithme décimal de x

lb x

log2 x}

logarithme binaire de x

colog x

cologarithme décimale de x

sin x

sinus de x

cos x

cosinus de x

tg x

tangente de x

ctg x

cotangente de x

sec x

sécante de x

cosec x

cosécantes de x

sh x

sinus hyperbolique de x

ch x

cosinus hyperbolique de x

th x

tangente hyperbolique de x

cth x

cotangente hyperbolique de x

sch x

sécante hyperbolique de x

csch x

cosécante hyperbolique de x

arcsin x

arc sinus de x, fonction inverse de sin x

arccos x

arc cosinus de x

arcctg x

arc tangente de x

arcctg x

arc cotangente de x

arcsec x

arc sécante de x

arccosec x

arc cosécante de x

lim x

limite de x

lim f (x)

x→0

limite de f (x) quand x tend vers a

limite supérieure de f (x) quand x tend vers a

$\stackrel{}{\underset{x\to a}{\lim }} f\left(x\right)$

limite inférieure de f (x) quand x tend vers a

$\stackrel{}{\underset{x\to \pm \infty }{\lim }} f\left(x\right)$

limite de f (x) quand x tend vers plus ou moins l'infini

limite supérieure de f (x) quand x tend vers plus ou moins l'infini

limite inférieure de f (x) quand x tend vers plus ou moins l'infini

max f (x)

maximum de f (x)

min f (x)

minimum de f (x)

| f (x) |

module dе f (x)

dérivée de f (x) par rapport à x

dérivée seconde de f (x) par rapport à x; dérivée seconde dе f (x) d'ordre deux par rapport à x

dérivée d'ordre n de f (x) par rapport à x

dérivée partielle de f (x, y) par rapport à x

$\frac{{\partial }^{2}f(x,y)}{\partial x\partial y}$

dérivée partielle d'ordre deux par rapport à x et y; dérivée partielle du deuxième ordre par rapport à x et y

∫ f (x) dx

intégrale indéfinie de f (x)

b

∫ f (x) dx

a

intégrale définie de f (x) de a à b

∫∫

intégrale double

∫∫∫

intégrale triple

$\iint \stackrel{\dots }{n}\int$

intégrale n-uple

$\underset{T\to 0}{\lim } {\int }_0^{t}f\left(x\right)dx$

limite quand T tend vers a de l'intégrale prise de 0 à T de la fonction f (x)

limite quand T tend vers l'infini de l'intégrale prise de 0 à T de la fonction f (x)
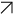