Тенденции и причины изменений глобального климата земли В современную эпоху

2.1. Исторические этапы
в изучении вариаций солнечной активности

2.1.1. Наблюдения солнечной активности

2.1.2. Измерения солнечной постоянной

2.2. Исторические этапы исследований инсоляции Земли

2.2.1. Низкочастотные изменения инсоляции
(история развития астрономической теории палеоклимата)

2.1.2. Высокочастотные изменения инсоляции

***

Солнце излучает энергию, которая обеспечивает Землю теплом и светом. Лучистая энергия Солнца является основным источником энергии гидрометеорологических и многих других процессов, происходящих в атмосфере, гидросфере, на земной поверхности. Энергия Солнца является важнейшим фактором развития жизни на Земле, обеспечивающим необходимые для жизни термические условия и фотосинтез. Поэтому изучение пространственных и временных изменений инсоляции имеет важное значение для исследования происходящих в географической оболочке Земли процессов, причин формирования и изменения климатических условий существования жизни на планете.

Годовой приход солнечной радиации на верхнюю границу атмосферы Земли (ВГА) составляет 5,49 × 1024 Дж. [1, 46, 203, 204]. Этот приход во времени не является постоянным, он подвержен межгодовым и многолетним (вековым и периодическим) вариациям. Вариации приходящей к Земле лучистой энергии в основном определяются двумя причинами, имеющими различную физическую природу. Одной из причин является изменение активности в излучении Солнца. Другой причиной, определяющей изменение приходящей к Земле энергии, являются небесно-механические процессы, вызывающие изменения элементов земной орбиты [114, 118–120] и наклона оси вращения. В соответствии с этими причинами, в разделе 2.1. излагается история изучения вариаций, связанных с изменением излучающей активности Солнца. В разделе 2.2. рассматривается история изучения вариаций, связанных с небесно – механическими процессами, и современное состояние этого вопроса.

2.1. Исторические этапы
в изучении вариаций солнечной активности

2.1.1. Наблюдения солнечной активности

В истории исследований излучательной способности Солнца (солнечной активности) можно выделить два основных этапа. Первый (с начала XVII до настоящего времени) отражает научные наблюдения за состоянием солнечной активности. Второй (с начала XX века до настоящего времени) этап включает еще и непосредственные измерения солнечной радиации. Эти основные этапы подразделяются на отдельные исторические фрагменты, маркируемые во времени характерными реперами, отражающими моменты определенных технических достижений в области наблюдения и измерения солнечной активности.

Относительно регулярные наблюдения Солнца ведутся на протяжении более четырех столетий. В результате этих наблюдений был определен 11-ти летний цикл солнечной активности, проявляющийся в квазипериодическом изменении числа солнечных пятен и составляющий основу представлений о Солнце и многих явлениях солнечно – земной физики (рис. 2.1). Эта цикличность в образовании пятен на Солнце является наиболее известным эффектом; она достаточно хорошо документирована и в астрономии представляет собой широко наблюдаемое явление. Однако, следует отметить, что непрерывные и достаточно точные ряды наблюдений солнечных пятен имеются только для периода немногим более ста лет. Данные для эпохи ранее 1850 года оказываются в значительной степени неопределенными. Для более отдаленных эпох существует мало или вообще нет доказательств того, что современный 11-ти летний цикл – постоянное солнечное явление [214, 215]. Тем не менее, солнечные пятна – это наиболее легко наблюдаемый индикатор уровня солнечной активности и источник наиболее длительно регистрируемых непосредственных данных об истории активности Солнца [25, 26, 267].

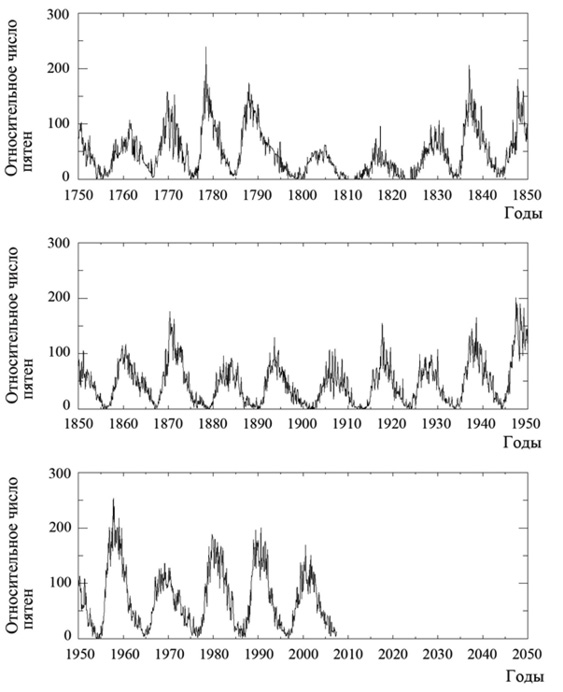
Рис. 2.1. Распределение солнечных пятен [298]

Достоверно известно, что телескоп был изобретен в Голландии в 1608 году. Исследование небесных объектов с помощью телескопа начали почти одновременно английский математик Томас Гарриот, немецкий ученый Симон Мариус и Галилео Галилей. Свои первые телескопические наблюдения Галилей обнародовал в начале 1610 года в книге «Sidereus Nuntius» («Звездный вестник»). Это были результаты телескопических наблюдений Луны, открытие четырех спутников Юпитера. Также Галилеем наблюдались в телескоп Венера и Сатурн. Ряд телескопических наблюдений завершился открытием темных пятен на Солнце. По собственному утверждению Галилея, он впервые заметил их в конце 1610 года [13] но, по-видимому, не обратил на них особенного внимания (в письме от 4 мая 1612 года он пишет, что наблюдал их восемнадцатью месяцами ранее; в «разговоре о двух системах» он отмечает, что видел их еще в то время, когда читал лекции в Падуе, т.е. не позже сентября 1610 года). Однако формальное объявление об открытии пятен на Солнце было сделано Галилеем в мае 1612 года, когда это открытие было сделано независимо от него Томасом Гарриотом в Англии, Иоаном Фабрицием в Голландии и иезуитом Христофором Шейнером в Германии и обнародовано Фабрицием в июле 1611 года [13]. Именно Шейнеру принадлежит честь открытия факелов. Кроме того, он произвел ряд наблюдений над движениями и появлением пятен [13].

О цикличности проявления солнечных пятен не было известно до 1843 г., когда немецкий астроном – любитель Генрих Швабе указал на явную 10-ти летнюю периодичность, выявленную на основании его 17-ти летних наблюдений. Это открытие, тем не менее, оставалось незамеченным до тех пор, пока известный немецкий географ Александр Гумбольдт не опубликовал выводы Швабе (по 25-ти летним наблюдениям) в своем многотомном труде «Космос», изданном в 1851 году [41, 102, 148].

С учетом полученных Швабе (и ставших известными) результатов, была разработана международная программа наблюдений Солнца (продолжающихся в настоящее время). Основной целью этой программы стали исследования и наблюдения для определения того, является ли найденная Швабе цикличность реальным и непрерывным эффектом. Инициатором и организатором этих наблюдений был Рудольф Вольф из цюрихской обсерватории (его показатель чисел солнечных пятен – индекс или числа Вольфа – используется и в настоящее время). Вольф провел обширные исследования исторических данных о регистрации солнечных пятен для определения существования цикла в прошлом. После длительных и целенаправленных исследований им были собраны исторические доказательства, относящиеся к промежутку времени между наблюдениями Швабе и открытием пятен при помощи телескопа (в начале XVII в.). Вольф пришел к заключению, что 11-ти летний цикл действительно существовал, начиная с 1700 г., а возможно, и раньше. Восстановленные им числа солнечных пятен за этот ранний период признаны реальными во всех последующих работах, посвященных истории Солнца. Более половины данных, приведенных на рис. 2.1, являются результатом этих исследований Вольфа.

Относительное число солнечных пятен (индекс Вольфа – W) вычисляется, как сумма числа пятен (a) и удесятеренного числа всех групп пятен (b), т.е. W = a + 10b [25, 217]. Или R = k (f + 10g) где f – число отдельных пятен, которые объединяются в g групп, k – эмпирический коэффициент [1, 11, 71, 74]. Важность этого индекса определяется, во-первых, его простотой. Во-вторых, тем, что его значения, благодаря работам Вольфа, известны с 1700 года – годичные данные или с 1749 г. – месячные данные [67, 71, 216, 240].

Около 160 лет назад было установлено, что 11-ти летний цикл солнечной активности проявляется не только в изменении числа солнечных пятен (факельных площадок и солнечных вспышек), но и в изменении во времени широты групп пятен (рис. 2.2). В 1852 году три исследователя: Эдуард Сабин в Англии, Рудольф Вольф и Альфред Готье из Швейцарии независимо друг от друга обратили внимание на определенное соответствие между периодическими изменениями солнечных пятен и земными магнитными явлениями. Кроме того, выяснилось, что их периоды одинаковы, и неизменно случается так, что в эпохи с большим количеством солнечных пятен на Земле отмечаются сильнейшие магнитные бури. Также совпадают и периоды ослабления этих явлений [13].

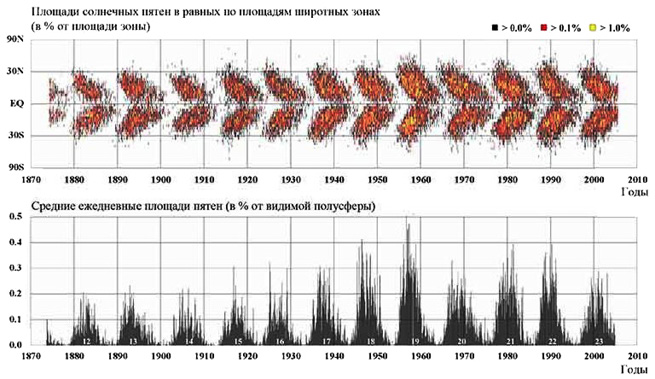
Рис. 2.2. Характер изменения широты групп пятен
в ходе 11-летнего цикла числа пятен [288, 298]

Это распределение было изучено английским исследователем Солнца Ричардом Кэррингтоном (результаты опубликованы в 1863 году в монографии «Наблюдение пятен на Солнце») из Королевской обсерватории Гринвича (Royal Greenwich Observatory). Он обнаружил, что в начале 11-ти летнего цикла пятна обычно появляются в относительно высоких широтах (в среднем на расстоянии ± 25°–30° от солнечного экватора), тогда как в конце цикла они концентрируются вблизи экватора (в среднем на широтах ± 5°–10°). Позже (1880 г.) этот эффект был детальнее исследован немецким ученым Густавом Шпёрером. Оказалось, что среднюю продолжительность 11-ти летнего цикла можно гораздо точнее определить по изменению широты групп солнечных пятен, чем по вариациям чисел Вольфа. Исследования Кэррингтона и Шперера, показывающие характер изменения широты групп пятен в ходе 11-ти летнего цикла числа пятен, наряду с открытием Швабе – Вольфа 11-ти летнего цикла образования пятен, представляют основные, достоверно известные закономерности в многолетней изменчивости солнечной активности [1, 25, 26, 217, 267].

В конце XIX века Густав Шпёрер и Эдвард Маундер при изучении архивов наблюдения Солнца обратили внимание на приблизительно 70-ти летний период (с середины XVII века), когда сообщений о солнечных пятнах практически не было [154, 254]. В опубликованных позже статьях Маундер сделал вывод о том, что в течение этого времени примерно с 1645 по 1715 гг., нормальный солнечный пятнообразовательный цикл был полностью или почти полностью подавлен. Он указал, что это явление, если оно реально, заставляет сомневаться в отношении постоянного характера 11-ти летнего цикла солнечной активности.

Более поздние исследования этого вопроса подтвердили справедливость вывода Маундера и выявили некоторые дополнительные факты, неизвестные во времена Маундера (например, по изучению частоты полярных сияний, для которой характерна высокая корреляционная связь с уровнем солнечной активности и др.). В течение всего периода (с 1645 по 1715 гг.) солнечная активность характеризовалась уровнями более низкими, чем минимумы современных циклов [154]. Поскольку относительные значения чисел пятен в этот период изменялись в пределах от 0 до 5, не представляется возможным выделить их максимальное значение, и вопрос о существовании 11-ти летнего цикла для этого периода, таким образом, остается открытым.

Регулярные наблюдения магнитных полей солнечных пятен, отрытых в начале прошлого столетия (1913 г.) американским астрономом Дж. Хейлом, привели к признанию реальности 22-х летнего цикла солнечной активности. Для 14-го (по цюрихской нумерации) цикла Хейл определил, что полярность магнитных полей ведущих (хвостовых) пятен северного (южного) полушария Солнца изменяется на противоположную при переходе от одного 11-ти летнего цикла к другому [153]. Первоначальная полярность восстанавливается, следовательно, через 22 года. В дальнейшем такие изменения наблюдались в течение всех последующих 11-ти летних циклов. В нечетных (по цюрихской нумерации) циклах полярность магнитного поля ведущих пятен групп северного полушария положительная (северная), а в четных циклах – отрицательная (южная). В южном полушарии отмечается противоположная картина [220].

Таким образом, 11-ти летний и 22-х летний циклы солнечной активности считаются (для настоящего времени) надежно установленными. Существование более длинных циклов солнечной активности является пока предположением. Так, например, рядом исследователей выделяется вековой (80–90-летний) цикл солнечных пятен – цикл Глейсберга [1, 216, 275]. Наиболее четко 80–90-летняя вариация выделяется по сумме среднегодовых чисел Вольфа в 11-ти летнем цикле или по максимальным их значениям. С 1749 года по среднегодовым относительным числам пятен было выделено два минимума и три максимума вековых циклов. Согласно цюрихской нумерации 11-ти летних циклов, минимумы были в 6-м и 14-м циклах, а максимумы в 3-м, 9-м и, вероятно, в 19-м циклах. При разложении чисел Вольфа на их основные составляющие – число групп пятен и среднюю продолжительность их существования, оказывается, что первая в основном показывает изменения со средним периодом 11 лет, а вторая – со средним периодом 80–90 лет. Из этого следует, что 11-ти летний цикл характерен для частоты явлений солнечной активности, а вековой – для их мощности (амплитуды). Однако окончательно вопрос о существовании вековой вариации солнечной активности не решен. Отдельными исследователями отмечается существование вариаций солнечной активности и с более длительными периодами, например 200-летний цикл Зюсса [1, 346].

В настоящее время ряд организаций проводит сбор данных и регулярные наблюдения солнечного цикла, и подсчет числа пятен на Солнце. Например, Solar Influences Data Analysis Center (SIDC) в Бельгии [292, 296]. В этом отделе физики Королевской обсерватории определяется так называемое международное число солнечных пятен – International Sunspot Number. Кроме этого, подсчет числа пятен ведется в National Oceanic and Atmospheric Administration (NOAA) в США [294]. Число пятен, определяемых в Национальном управлении океанических и атмосферных исследований, имеет название NOAA sunspot number.

2.1.2. Измерения солнечной постоянной

Мерой приходящей на верхнюю границу атмосферы солнечной радиации является солнечная постоянная. Под солнечной постоянной понимается суммарный поток солнечного излучения, проходящий за единицу времени через единичную площадку, ориентированную перпендикулярно потоку на расстоянии 1 а.е. от Солнца вне земной атмосферы [3, 4, 71, 129]. Солнечная постоянная определяется соотношением:

$S_0 = \frac{\sigma R^2 \times T_{эфф}^4}{A^2},$

где σ – постоянная Стефана – Больцмана, А – астрономическая единица, R – радиус Солнца, Тэфф – эффективная температура фотосферы [1]. По нашему мнению, правильнее было бы называть солнечную постоянную интенсивностью суммарного потока солнечного излучения.

История измерений солнечной постоянной включает измерения с земной поверхности, из атмосферы (с самолетов и аэростатов) и внеатмосферные измерения (со спутников и ракет) [132]. В метеорологии радиометрические измерения начались в конце XIX столетия. Для решения проблемы точности и обеспечения возможности сравнения результатов измерений на различных приборах и на различных станциях были введены специальные радиометрические шкалы. В течение многих лет эти стандарты или шкалы подвергались ряду ревизий, отражающих усовершенствования в радиометрии. До середины прошлого столетия обычно использовались две такие шкалы: Онгстрёма (1905 г.) и Смитсонианская шкала (1913 г.). Накануне Международного геофизического года была введена новая Международная пиргелиометрическая шкала (МПШ, 1956), основанная на этих шкалах.

В начале прошлого столетия в Смитсонианской астрофизической обсерватории началось проведение серии высокогорных измерений солнечной постоянной. Согласно полученным (более чем за полвека) данным, вариации солнечной постоянной составили от 0,1 до 1%. Проведенными измерениями также обнаружено долговременное увеличение (тренд) среднего значения солнечной постоянной примерно на 0,25% за 50 лет [218]. Анализ полученных результатов за четыре солнечных цикла (с 1908 по 1952 гг.) показал, что пределы возможных вариаций солнечной постоянной находятся в диапазоне ± 1% (от средней величины солнечной постоянной). Это было подтверждено и повторным анализом полученных в Смитсонианской обсерватории результатов. Средняя многолетняя величина солнечной постоянной, полученная в Смитсонианской обсерватории, составила 1,94 кал/см2 × мин или 1352 Вт/м2 [71, 98, 99].

Исторически первые прямые измерения солнечной постоянной вне тропосферы были выполнены в Ленинградском университете в 1961 году (группой под руководством К.Я. Кондратьева). Комплекс приборов поднимался аэростатом на высоту до 32 км. Всего до 1967 года было проведено 28 подъемов аэростата. Методика наблюдений и результаты подробно изложены в ряде публикаций [71, 76–78, 98, 132]. В результате этих измерений была обнаружена весьма заметная вариация солнечной постоянной (2,5%), вероятно, связанная с ошибками в измерениях. Среднее значение солнечной постоянной по результатам всего комплекса измерений составило 1356 ± 14 Вт/м2.

В 1966 году Лабораторией реактивного движения (Калифорнийский технологический институт) и лабораторией Эппли была предложена программа измерений солнечной постоянной, в рамках выполнения которой Драммондом (Drammond) было получено среднее значение солнечной постоянной по результатам шести полетов на реактивном исследовательском самолете NASA равное 1359 ± 13 Вт/м2. В 1968 году Кендaлл (Kendall) провел измерения с радиометром PACRAD c борта самолета NASA. Окончательное значение, полученное в результате этих измерений, оказалось равным 1373 ± 14 Вт/м2. Среднее значение по всем измерениям с самолетов составило 1378 ± 26 Вт/м2.

В период 1968–1969 гг. Р. Уилсоном (Willson) также были проведены аэростатные измерения солнечной постоянной. Среднее значение солнечной постоянной (по трем аэростатным измерениям) составило 1373 ± 14 Вт/м2. В 1969 году им же было выполнено определение солнечной постоянной вблизи максимума цикла №20 и получено значение равное 1369 Вт/м2. Точность аэростатных измерений оценивается величиной 0,2–0,5% [197, 362, 363, 365].

Измерения вариаций солнечной постоянной с использованием космических аппаратов обладают большей достоверностью, прежде всего, в связи с тем, что они проводятся за пределами земной атмосферы. Эти измерения, во-первых, исключают атмосферную экстинкцию (поглощение и рассеяние) и, во-вторых, осуществляются в течение многих суток. Первое длительное измерение солнечной постоянной за пределами земной атмосферы выполнено в эксперименте, поставленном Лабораторией реактивного движения на искусственных спутниках Земли «Маринер – 6» и «Маринер – 7» в 1969 году. Измерения показали, что величина солнечной постоянной не изменялась больше, чем в пределах точности измерений (около ± 0,25%) вблизи максимума солнечного цикла, причем в течение этого времени суточное число солнечных пятен принимало как экстремально большие, так и экстремально малые значения [98, 157, 369].

В соответствии с реализацией программы эксперимента «Радиационный баланс Земли» (ERB), проведенного с борта космического аппарата «Нимбус – 6», запущенного в 1975 г., были получены значения солнечной постоянной в диапазоне от 1388 до 1392 Вт/м2. В 1976 году проводились одновременные измерения солнечной постоянной с зондирующей ракеты (высота около 100 км) и космического аппарата «Нимбус – 6». Среднее значение по ракетным данным составило 1376 ± 7 Вт/м2, по данным космического аппарата – 1376±14 Вт/м2. С учетом поправок абсолютное значение определяется в 1367 Вт/м2. Эта величина сравнима со значением 1369 Вт/м2, полученным Уилсоном в 1969 г. Поскольку эти два измерения, совершенные в минимуме и максимуме солнечной активности, согласуются в пределах ошибок абсолютного радиометра, то это показывает, что солнечная постоянная оставалась неизменной в пределах 0,75% в течение второй половины цикла №20 [157]. Среднее значение скорректированных величин солнечной постоянной, полученных при измерениях с помощью самолетов, ИСЗ «Маринер – 6», «Маринер – 7», «Нимбус – 6» и ракет («Аэроби»), составило для периода 1962–1980 гг. 1369 ± 6 Вт/м2 [98]. Данные ракетных наблюдений солнечной постоянной, проведенных в 1976 году с помощью четырех абсолютных радиометров различной конструкции, приводятся в работе Кондратьева и Никольского [77]. Значение, осредненное по записям трех согласованных радиометров, оказалось равным 1367 ± 6 Вт/м2.

По оценкам Фрёлиха (Frӧhlich), основанным на обзоре всех измерений, выполненных с помощью самолетов, аэростатов и космических аппаратов, наиболее вероятное значение солнечной постоянной равно 1373 ± 20 Вт/м2 [197]. Это среднее сравнимо со средневзвешенным значением 1370 ± 1 Вт/м2, которое было получено по всем измерениям, включая данные ракетного эксперимента в 1976 г. и исправленные данные эксперимента ERB («Нимбус – 6»). При учете всех данных за 1976 г. величина солнечной постоянной была заключена в диапазоне 1368–1379 Вт/м2. При этом отмечается, что данные измерений с аэростата и самолета заметно отличаются от данных космических измерений (табл. 2.1).

Таблица 2.1

Сравнение результатов определения солнечной постоянной,
полученных различными экспериментальными методами [197]

Числа в скобках соответствуют стандартным отклонениям от средневзвешенных значений. Измерения при помощи самолета производятся на высотах 10–12 км, на аэростатах – 20–36 км.

Начиная с запуска американских спутников «Нимбус – 7» (1978 г.), а затем и SMM (1980 г.), оснащенных полостными радиометрами (радиометр H – F из серии ЕРБ и активный полостной радиометр АКРИМ соответственно), начался новый этап в измерении солнечной постоянной (рис. 2.3)

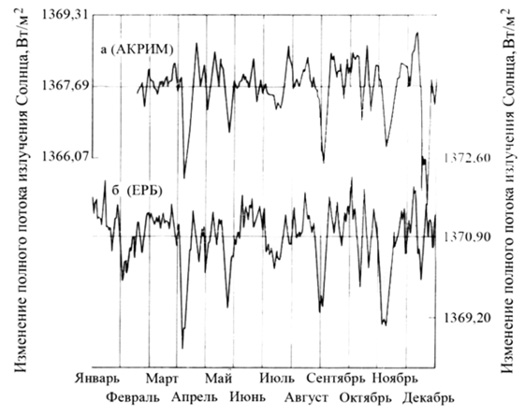
Рис. 2.3.Сопоставление полных потоков солнечного излучения,
измеренных в 1980 году на спутниках SMM (а) и «Нимбус – 7» (б) [98]

Впервые за всю историю определения солнечной постоянной ее измерения достигли точности в сотые доли процента [268, 270, 271, 273, 321, 338, 364, 366, 367, 370, 371]. Совершенствование измерений солнечной постоянной в это время определяется в основном тремя факторами: усовершенствованием измерительных приборов (пиргелиометры) и увеличением точности каждого измерения; выносом приборов за пределы атмосферы (чем полностью устранен важнейший источник ошибок наземных наблюдений – атмосферная экстинкция); автоматизацией наблюдений и широким применением компьютерной техники. В результате достигнута высокая внутренняя точность наблюдений на одном и том же спутниковом приборе в ± 0,3–0,7 Вт/м2, что составляет 0,02–0,05% значения солнечной постоянной [98]. Необходимость такой точности определяется полученными результатами, подтверждающими весьма малые изменения потока солнечного излучения.

При достигнутой внутренней точности и обязательном применении контроля чувствительности оказалось возможным определить точное значение солнечной постоянной и наблюдать ее вариации – суточные, недельные и более долговременные (например, спутниковые наблюдения в экспериментах по измерению солнечной постоянной для программы NASA по исследованию активного Солнца и для космической программы «Шатл»). При этом, наиболее информативный материал был получен с «Нимбуса – 7» (запущен в ноябре 1978 года) и SMM – Solar Maximum Mission (запущен в феврале 1980 года). Абсолютное значение солнечной постоянной в рассматриваемый период было заключено в пределах 1367–1373 Вт/м2, а среднее значение – 1370,59 Вт/м2 – в шкале прибора ЕРБ на «Нимбусе – 7» и 1370,62 Вт/м2 – на SMM. Определено уменьшение солнечной постоянной от максимума 21-го цикла (1980 г.) к его минимуму (1986 г.) примерно на 0,15%, или 2 Вт/м2. Годовой ход в среднем составил 0,02% [98, 364, 367].

К настоящему времени получен непрерывный ряд непосредственных измерений солнечной постоянной, выполненных несколькими специальными космическими аппаратами с 1978 года [239, 361, 368]. Эти (технически сложные) измерения выполнены для трех полных циклов солнечной активности (21–23) и продолжаются в текущем 24 цикле (рис. 2.4).

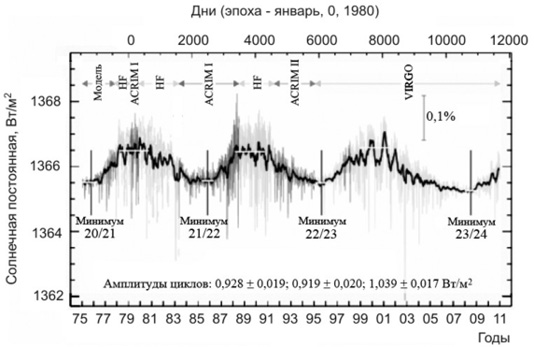
Рис. 2.4. Результаты спутниковых измерений солнечной постоянной.
Данные сайта мирового радиационного центра –
World Radiation Center – Швейцария [295]

Амплитуда 11-ти летних сглаженных циклических вариаций солнечной постоянной, по данным этих измерений, составляет около 1,0 Вт/м2, или приблизительно 0,07% от среднего значения солнечной постоянной (рис. 1.4). Среднее для минимумов (21–23 циклы) значение составляет 1365,458 ± 0,016 Вт/м2, среднее значение солнечной постоянной для 22-го цикла равно 1365,99 Вт/м2, для 23-го цикла – 1365,82 Вт/м2 [1, 295].

В настоящее время с учетом того, что солнечная постоянная не является неизменной величиной, ее определение изменилось. Полное количество солнечной энергии по всему спектру, падающее за единицу времени на единицу площади, перпендикулярную солнечным лучам, на среднем расстоянии Земли от Солнца за пределами земной атмосферы (под которым ранее понималась солнечная постоянная) теперь обозначается как TSI (суммарный или общий поток излучения, хотя по нашему мнению, это его интенсивность). Под солнечной постоянной понимается среднее многолетнее значение TSI, общего потока излучения. Иными словами, TSI – это нормированная по расстоянию (1 а.е.) инсоляция Земли. Принятое IPCC значение солнечной постоянной составляет 1361 Вт/м2 [269, 307, 308]. Реконструированные значения TSI [318] рекомендуются IPCC в проекте физико-математических моделей климата CMIP–5 в качестве данных радиационного блока [287]. Они представлены с годовым разрешением по времени с 1610 г. и с месячным разрешением с 1882 г. Реконструкция выполнена на основе данных радиометрических наблюдений с 1978 г. (рис. 2.4), чисел Вольфа (рис. 2.1) и чисел факельных вспышек [318]. Среднее многолетнее значение TSI, по данным реконструкции, составляет 1361 Вт/м2 [308]. То есть, в качестве входного энергетического сигнала в современных моделях климата используются данные TSI реконструированные по вариациям солнечной энергии, физическую природу которых (до 1978 года) составляет изменение активности Солнца.

Следует отметить, что поиски связи 11-ти летней вариации TSI с изменениями климатических характеристик, геофизическими и биофизическими параметрами проводились на протяжении всего периода с момента обнаружения этого цикла солнечной активности (т.е. полутора столетий). Результаты этих исследований представлены в многочисленных публикациях. Однако, в связи с получением малых значений амплитуды солнечной постоянной в 11-ти летнем цикле и нестабильностью амплитудно-периодических характеристик, интерес к исследованию солнечно-земных связей в этом диапазоне в настоящее время существенно снизился. Кроме отсутствия перспектив по модуляции климатических изменений 11-ти летней вариацией TSI, снижению ее значимости способствовали возрастающая неоднозначность прямых корреляционных сопоставлений при удлинении рядов наблюдений, а также отсутствие убедительных доказательств существования этого цикла в прошлом (его устойчивости во времени).

2.2. Исторические этапы исследований инсоляции Земли

В истории исследований изменений инсоляции Земли, связанных с небесно-механическими процессами, можно выделить два основных этапа. Один – более ранний и более продолжительный – отражает исследования низкочастотных (вековых) вариаций и связан с необходимостью объяснения причин изменения палеоклимата. Другой этап начался относительно недавно и связан с исследованием высокочастотных (периодических) вариаций инсоляции в связи с поисками причин изменения современного климата.

2.2.1. Низкочастотные изменения инсоляции
(история развития астрономической теории палеоклимата)

Вариации солнечной радиации, связанные с небесно-механическими процессами, определяются расчетными методами. Под солярным климатом Земли понимается рассчитываемое теоретически поступление и распределение солнечной радиации на верхней границе атмосферы (ВГА) или на поверхности Земли без учета атмосферы [3, 204]. При изучении вековых (низкочастотных) вариаций солнечного потока учитываются подверженные вековым возмущениям такие астрономические элементы земной орбиты как, долгота перигелия и эксцентриситет, а также наклон оси вращения Земли имеющие весьма значительные по продолжительности периоды изменений [114, 207–209, 224–226].

История изучения вековых (низкочастотных) вариаций солнечной радиации, определяемых небесно-механическими процессами, отражает развитие исследований, относящихся к астрономической теории климата [46, 84, 112, 113, 118–120, 202, 299, 300]. Появлению астрономической теории климата предшествовало развитие представлений о распространении покровных оледенений в истории Земли. Астрономическая теория климата возникла как необходимость объяснения и физического обоснования ледниковой теории.

Начало истории астрономической теории климата относится к середине XIX века и связано с работами Ж. Адемара, в которых формулируются представления о том, что основной причиной древних оледенений могли быть нарушения в закономерном ходе обращения Земли вокруг Солнца [219]. Согласно представлениям Адемара, ледниковые климаты были функцией 22 000 летнего цикла прецессии, и оледенения происходили поочередно через каждые 11 000 лет, охватывая то одно полушарие, то другое – в зависимости от того, на какое из них приходился период продолжительных зимних сезонов (зимний сезон совпадал с положением Земли вблизи афелия). Основополагающая идея Ж. Адемара о том, что северное и южное полушарие Земли нагреваются и охлаждаются поочередно, была подвержена сомнению немецким естествоиспытателем А. Гумбольдтом и английским астрономом Дж. Гершелем. Гумбольдт, например, справедливо отмечал, что средняя температура любого из полушарий определяется не числом часов (суток) теплого и холодного сезона года, а количеством калорий солнечной энергии, которое оно получает за год [41]. Тем не менее, предположение Ж. Адемара о связи возможных климатических изменений с определенными астрономическими явлениями (предварение равноденствий) стало основой для дальнейшего развития представлений об астрономических факторах изменения климата [15, 16, 60, 114, 225, 227; 299, 300] Представления о связи периодов распространения древних оледенений с астрономическими механизмами получили развитие в работах шотландского ученого Д. Кролля [114, 211, 245]. В качестве основополагающего астрономического фактора в представлениях Д. Кроля (наряду с прецессионным циклом) принимается изменчивость эксцентриситета земной орбиты. Используя формулы У. Леверье [320], Д. Кролль рассчитал эксцентриситет земной орбиты для ряда моментов за последние три миллиона лет (при этом учитывались семь известных в то время планет). В результате проведенных расчетов им был определен циклический характер вариаций эксцентриситета. Анализируя полученные данные, Д. Кролль пришел к предположению о том, что причина ледниковых эпох может быть связана с условиями максимально вытянутой орбиты. Из работ У. Леверье следовало, что общее количество энергии, получаемой Землей за год, практически не зависит от изменений эксцентриситета ее орбиты. Однако Кролль показал, что в сочетании с изменением отражательной способности Земли (альбедо) интенсивность радиации, которая поступает на Землю в астрономические полугодия, от изменений эксцентриситета зависит весьма заметно. В результате Д. Кроллем была предложена теория, объясняющая глобальные изменения климата (ледниковые и межледниковые эпохи), основу которой составили сезонные эффекты изменений эксцентриситета земной орбиты, учет влияния альбедо и положительных обратных связей [15, 16, 109, 114, 245, 299, 300, 324]. Представления Д. Кролля, основу которых составили два астрономических фактора – прецессионный цикл и периодическое изменение формы земной орбиты были –опубликованы в «Философском журнале» в 1864 году.

Вековые колебания поступающей к Земле солнечной радиации в виде математической задачи были рассмотрены в работах Л. Мича [323]. Им были получены формулы, связывающие поступающую радиацию (для любой широты) с вековыми колебаниями эксцентриситета, долготы перигелия и наклона эклиптики. Р. Болль [223], придал теории Д. Кролля математическую форму при учете двух параметров: эксцентриситета и прецессии. При этом в качестве влияния на общее количество солнечной энергии, получаемой отдельными полушариями, учитывался третий астрономический фактор – наклон эклиптики. К развитию астрономической теории также относятся работы Е. Кельверуэлла [246, 247], Р. Хэргривса [281], Н. Экхольма [255], но математическая часть задачи наиболее детально исследована в работах М. Миланковича [16, 109, 114, 119, 120, 166, 211, 227, 324].

Таким образом, к концу XIX века было известно, что распределение инсоляции по поверхности Земли (точнее земного шара, без учета атмосферы) зависит от трех орбитальных характеристик: эксцентриситета орбиты, наклона оси вращения и положения точек равноденствия в ее прецессионном цикле (вариации, определяемые эллипсоидальной формой Земли, на этом этапе не учитывались). В начале XX века появились работы немецкого математика Л. Пильгрима, в которых были изложены результаты новых расчетов этих астрономических характеристик («Опыт числовой разработки проблемы ледниковых периодов») за период времени в 1010 тысячелетий до 1850 г. н.э. [339]. В связи с этим расчет количества поступающей солнечной энергии стал принципиально возможным.

Расчеты вековых изменений астрономических элементов Л. Пильгрима (за 600 000 лет), были пересчитаны В. Мишковичем (директором астрономической обсерватории в Белграде). Эти данные стали основой для расчетов М. Миланковичем вековых вариаций инсоляции Земли. В своих расчетах В. Мишкович исходил из вычислений орбитальных характеристик и масс планет, выполненных У. Леверье. Л. Пильгрим использовал данные Ж. Стоквелла [349] уступающие по точности расчетам У. Леверье. Точность в расчетах В. Мишковича составляла: для эксцентриситета – до 4-х десятичных знаков, для наклона эклиптики – до секунд, для долготы перигелия – до минут для периода времени по меньшей мере 100 000 лет до и после эпохи, относящейся к началу 1800 года.

Следует, однако, отметить, что в то время С. Ньюкомбом [330] были составлены чрезвычайно точные таблицы движения планет (учитывающие Уран, Нептун и некоторые спутники планет), которые использовались в астрономии до середины XX века, однако М. Миланкович по тем или иным причинам в своих расчетах ими не воспользовался. Расчеты У. Лаверье основывались на вековых возмущениях, рассчитанных Ж. Лагранжем [311]. Значения масс планет и те цифровые данные, которыми Лагранж воспользовался для установления начальных условий, были недостаточно точны (это отмечает и М. Миланкович). Из известных теперь девяти планет Лагранж мог принять во внимание только шесть. Уран был открыт (Дж. Гершелем в 1781 году) во время выполнения расчетов Лагранжем, и элементы этой новой планеты не были определены даже приблизительно. Не было известно ничего и о ее спутниках. Нептун будет открыт (на основе расчетов У. Лаверье, связанных с возмущением в орбитальном движении Урана) только в 1846 году. Марс считался не имеющим спутников. Поэтому для определения масс двух планет (Марс, Уран) Лагранж мог опираться на грубо приближенные данные. Тем не менее, ему удалось, хотя и приблизительно, определить границы, между которыми могут изменяться эксцентриситеты орбит планет и наклоны плоскостей их орбит к плоскости эклиптики. Принципиально важным в контексте данного обзора представляется полученный Лагранжем вывод о том, что большие полуоси орбит не подвергаются вековым изменениям, который позднее был включен П. Лапласом в теорему устойчивости Солнечной системы [9, 48, 49, 87, 312].

М. Миланковичем были определены климатические (для солярного климата) эффекты вековых вариаций трех астрономических элементов: наклона эклиптики (ε), эксцентриситета (е) и долготы перигелия (П). Так, увеличение наклона оси вращения Земли (относительно перпендикуляра к плоскости эклиптики) приводит к сокращению годовой суммы радиации в экваториальной области и ее увеличению в полярных областях, то есть происходит сглаживание различий между экваториальной областью и полярными районами. Уменьшение наклона ведет к обратным результатам, усиливая широтные контрасты в распределении солнечной радиации на земной поверхности (без учета атмосферы). При ε = 0, когда оба полюса в течение всего года остаются неосвещенными, широтные контрасты максимальны [114]. Изменения наклона оси вращения имеют относительно правильный колебательный характер со средним периодом около 40 000 лет. В течение этого периода широтные различия достигают один раз максимума (при наименьшем наклоне эклиптики), причем сезонные различия в это время достигают своего минимума, и один раз, – через 20 000 лет – минимума (при наибольшем наклоне), когда сезонные различия выражены максимально. Эти явления повторялись бы периодически, если бы на них не накладывались влияния других астрономических элементов [114].

Годовой ход приходящей солнечной радиации также определяется продолжительностью летнего и зимнего сезонов (полугодий), которая является функцией двух элементов земной орбиты – эксцентриситета (е) и долготы перигелия (П). Вследствие изменчивости элементов е и П, разность в приходе радиации между летним и зимним сезоном (полугодиями) является функцией времени. Так, долгота перигелия приблизительно за 21 000 лет увеличивается почти равномерно на 360, так как перигелий за это время с почти равномерной скоростью описывает полный круг. Величина эксцентриситета (е) также испытывает колебания с периодом около 92 000 лет (со значительно меньшей амплитудой), оставаясь заключенной между 0 и 0,0677. Изменение разности в продолжительности летнего и зимнего сезонов зависит от обоих факторов, но влияние первого из них значительно сильнее. Вследствие этого, величина разности (между приходом в летнее и зимнее время) колеблется около некоторого среднего значения с периодом в 21 000 лет, а изменчивость амплитуды всех этих колебаний характеризуется периодом около 46 000 лет [114].

Зависимость векового хода приходящей радиации от изменений долготы перигелия (долгота перигелия орбиты – угол между направлением от Солнца на перигелий и точку весеннего равноденствия – в настоящее время равен 102°08) выражается следующим образом. Разность продолжительности летнего и зимнего полугодий равняется 0 только при долготе перигелия равной 0° (перигелий совпадает с точкой весеннего равноденствия) и при долготе равной 180° (перигелий совпадает с точкой осеннего равноденствия; равноденственные точки – точки пересечения земной орбиты с плоскостью небесного экватора). При этом суммы приходящей за полугодия солнечной энергии равны как за полугодия, так и для полушарий. Широтные различия в поступающей на верхнюю границу атмосферы Земли радиации в этих случаях максимальные (рис. 2.5).

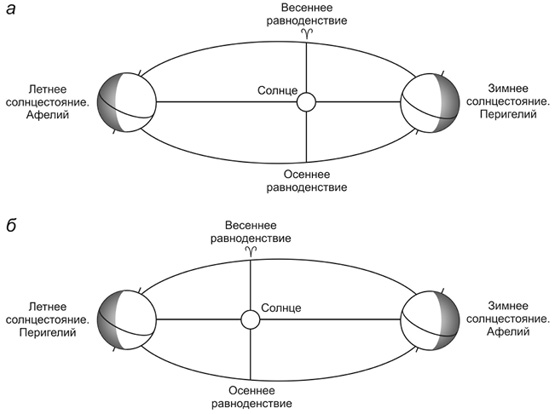
Рис. 2.5. Конфигурации Земли и Солнца:
а – при соединении перигелия с точкой зимнего солнцестояния
(долгота перигелия 90°);
б – при соединении перигелия с точкой летнего солнцестояния
(долгота перигелия 270°)

При увеличении долготы перигелия от 0° до 90° продолжительность летнего полугодия северного полушария увеличивается, а зимнего сокращается. В соответствии с этим, интенсивность солнечной радиации в летний период уменьшается, а в зимний – увеличивается. При долготе перигелия равной 90° (перигелий совпадает с точкой зимнего солнцестояния) продолжительность летнего полугодия в северном полушарии достигает максимума, а средняя интенсивность радиации сокращается летом до минимума, увеличиваясь до максимума зимой. По нашим расчетам [182], это событие имело место около 1250 г. н.э. (рис. 2.6).

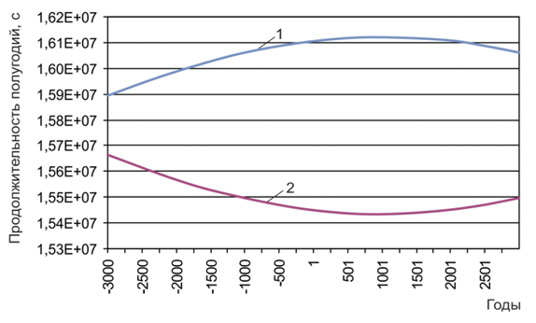
Рис. 2.6. Продолжительность (в секундах) астрономических полугодий:
1 – летнее полугодие в северном полушарии
(зимнее полугодие в южном полушарии),
2 – зимнее полугодие в северном полушарии
(летнее полугодие в южном полушарии)

Таким образом, сезонные контрасты в это время минимальные. Это верно, однако, только для северного полушария. В южном полушарии продолжительность летнего полугодия (совпадает с зимним полугодием в северном полушарии) сокращается, в то время как количество радиации, получаемой южным полушарием за это короткое лето, равно тому количеству, которое получает северное полушарие за свое лето, более продолжительное. Поэтому в южном полушарии более короткое летнее полугодие в это время характеризуется большей интенсивностью приходящей солнечной радиации, а более продолжительное зимнее полугодие – меньшей. Следовательно, сезонные различия в южном полушарии в это время максимальные (в отличие от северного полушария).

При долготе перигелия равной 180° (перигелий совпадает с точкой осеннего равноденствия) летнее и зимнее полугодие имеют равную продолжительность в северном и южном полушариях. Суммы приходящей за полугодия солнечной энергии равны, как за полугодия, так и для полушарий. Широтные различия в поступающей на верхнюю границу атмосферы Земли радиации в этих случаях максимальны. При долготе перигелия равной 270° (перигелий совпадает с точкой летнего солнцестояния) продолжительность летнего полугодия в северном полушарии минимальная, и противоположность между летним и зимним сезонами (полугодиями) выражена наиболее резко. В южном полушарии для этой долготы перигелия отмечается обратная ситуация – продолжительный летний сезон (с меньшей интенсивностью приходящей радиации) и менее продолжительный – зимний (с большей интенсивностью приходящей радиации). Сезонные контрасты при этом сглаживаются.

Таким образом, широтные различия максимальны при положении перигелия в равноденственных точках и сглаживаются при положении перигелия в точках солнцестояния. При этом, если перигелий находится в точке зимнего солнцестояния, сезонные различия в южном полушарии выражены наиболее контрастно, а в северном они сглаживаются. При положении перигелия в точке летнего солнцестояния ситуация становится обратной. В этом случае сезонные контрасты максимально выражены в северном полушарии и сглаживаются в южном полушарии [15, 60, 114, 118, 162, 299].

На основе расчетов вековых изменений астрономических элементов (выполненных В. Мишковичем) М. Миланковичем были рассчитаны значения летней инсоляции для параллели 65° северного полушария за последние 650 000 лет. Полученный Миланковичем график инсоляции (в значениях широтных эквивалентов) впервые был опубликован в 1924 году в работе В. Кёппена и А. Вегенера [310] «Климаты прошлого» (рис.2.7). Под эквивалентными широтами для 65° с. ш. понимаются широты, на которых в настоящее время за летнее калорическое полугодие поступает столько же солнечной радиации, сколько в прошлом поступало на широте 65° с. ш. Увеличение эквивалентной широты означает сокращение поступающей радиации, и наоборот (например, поступающая к Земле солнечная радиация на 65° с.ш. 590 000 лет назад, характерна для широты 72° с.ш. в эпоху 1800 г.).

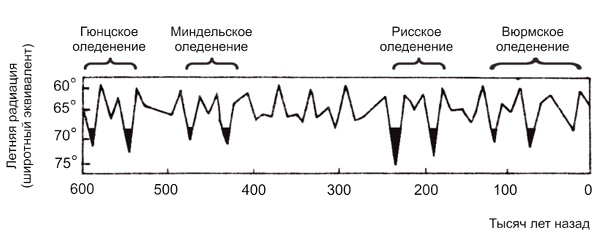
Рис. 2.7. Амплитуды вековых отклонений летних сумм радиации
для 65° с.ш. в значениях широтных эквивалентов [114]

Вместо расчета сумм тепла за летнее и зимнее полугодия, М. Миланкович использовал калорические полугодия. Калорические полугодия определяются как полугодия одинаковой продолжительности ($\frac{{Т}_o}{2}$), когда на данной широте любое значение суточной инсоляции в летнее полугодие больше любого значения суточной инсоляции в зимнее полугодие. Продолжительность тропического года считалась постоянной. При расчетах использовались канонические единицы (величина солнечной постоянной равная 2 кал/мин × см2 или 1395,6 Вт/м2 соответствовала 1 канонической единице, продолжительность тропического года 100 000 каноническим единицам). В дальнейшем М. Миланковичем были рассчитаны вариации инсоляции для восьми параллелей, располагающихся между 5° и 75° северной широты. Основные результаты его исследований изложены в работе «Математическая климатология и астрономическая теория изменения климата» [114].

Расчеты, произведенные М. Миланковичем, в дальнейшем выполнялись с уточнениями рядом авторов. Эти расчеты основывались на новых решениях теории вековых возмущений, полученных для всей Солнечной системы в 1950 году Д. Брауэром и А. Ван Вуркомом [237]. В расчетах использовались последние данные о массах и движении планет, учитывались эффекты второго порядка, вызванные, например, долгопериодическими вариациями в движении Юпитера и Сатурна.

Детальные расчеты приходящей на верхнюю границу атмосферы (ВГА) солнечной радиации провели советские астрономы Ш.Г. Шараф и Н.А. Будникова [207–209]. Ими были обнаружены ошибки в исходных значениях долготы узлов Венеры и Земли, использованных Д. Брауэром и А. Ван Вуркомом. На основе исправленных значений Ш.Г. Шараф и Н.А. Будниковой были пересчитаны постоянные интегрирования и выведены тригонометрические формулы для прецессии и наклона оси вращения, которые включали члены второго порядка для эксцентриситета и наклона. В результате ими были рассчитаны вариации инсоляции на период 30 млн. лет в прошлое и на 1 млн. лет в будущее. Оказалось, что значения эксцентриситета колебались в пределах 0,0007–0,0658 (в настоящее время 0,01675), преимущественно с периодами около 0,1; 0,425 и 1,2 млн. лет. Изменения величины наклона оси вращения происходили с периодами около 41 и 200 тыс. лет и определялись пределами от 22,068° до 24,568°. Отклонения величин е × sin П от его значения в 1950 году колебались в пределах от +0,03 до –0,07 со средним периодом около 21 тыс. лет. Вариации эквивалентных широт определялись пределами 58–79° (довольно значительно) с преобладающими периодами в 41 тыс. лет и 1,2 млн. лет. Построенные Ш.Г. Шараф и Н.А. Будниковой графики хода эквивалентных широт приведены на рис. 2.8.

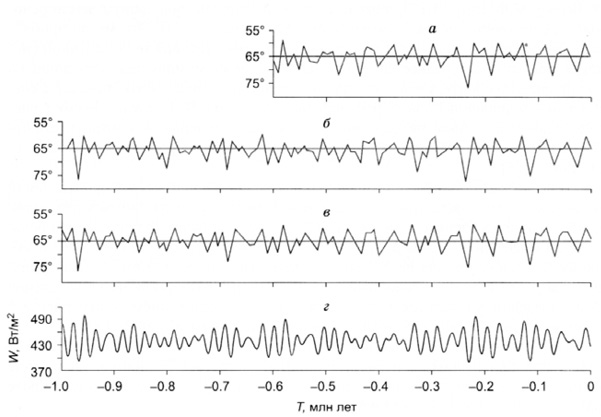
Рис. 2.8. Изменение инсоляции
за летнее калорическое полугодие для широты 65о северного полушария
по данным разных исследователей [113]: а – [114]; б – [237]; в – [207]; г – [228].
По оси абсцисс отложено время в тысячелетиях от 1950 г.;
по оси ординат: а, б, в – инсоляция в эквивалентных широтах
в течение летнего полугодия, г – среднемесячная инсоляция в июле W (Вт/м2)

С использованием полученных Ш.Г. Шараф и Н.А. Будниковой значений изменений наклона оси, эксцентриситета и долготы перигелия в Институте океанологии Российской Академии Наук были рассчитаны значения инсоляции на миллион лет в прошлое и будущее относительно современной эпохи (начало 1950 г.) с шагом по времени в 5 тыс. лет и по широте в 10° [118, 120].

Суммарная за калорические полугодия радиация рассчитывалась на основе соотношения:

(2.1) $Q_{S,W}=\frac{I_0{T}_0}{2\mathrm{\pi }}\left[S(\phi ,\epsilon )\pm \sin \left(\phi \right)\sin \left(\epsilon \right)\pm \frac{4}{\mathrm{\pi }}e \sin \left(П\right)\sin \left(\phi \right)\right],$

где I0 солнечная постоянная (равная 2 кал/мин × см2 или 1395.6 Вт/м2), T0– продолжительность тропического года (принимается постоянной), S – функция, описывающая распределение годовой инсоляции по меридиану, φ – географическая широта, П – долгота перигелия, e – эксцентриситет, ε – наклон эклиптики. Из формулы (2.1) видно, что величины Qs,w зависят от наклона оси ε и от элементов земной орбиты r0 (через l0 и T0), e и П [118]. Расчеты с использованием формулы (2.1) показали, что аномалии инсоляции за калорические полугодия максимальны в летних полярных областях, где они достигают значений ± 250 МДж/м2, и в общем убывают в сторону зимних полярных районов. Отмечается, что изменение аномалий имеет квазипериодический характер с периодом около 40 000 лет [118, 120, 360].

Также повторные расчеты вековых изменений элементов земной орбиты и инсоляции были выполнены А. Вернекаром [359]. Позднее А. Берже [225, 226] предложил улучшение для решения Д. Брауэра и А. Ван Вуркома (включив для эксцентриситета и наклона оси члены третьего порядка) и рассчитал вариации элементов орбиты и инсоляции. Сравнение рассчитанных вариаций солнечной радиации приведено на рис. 2.8. Из представленных графиков видно, что последний максимум в поступлении солнечной радиации для северного полушария отмечался около 10 тыс. лет назад (соответствует общим представлениям о времени деградации покровного оледенения в Европе и Северной Америке и приблизительно положению перигелия орбиты Земли в точке весеннего равноденствия). С этого времени происходит постепенное сокращение поступающей солнечной радиации, которое, по расчетам Ш.Г. Шараф и Н.А. Будниковой, будет продолжаться еще около 10 тыс. лет [207]. В это время перигелий земной орбиты будет располагаться вблизи точки весеннего равноденствия [162].

В наше время И.И. Смульским и О.И. Кротовым предложен алгоритм расчета инсоляции, основанный на точном решении задачи движения 2-х тел (Земли и Солнца). Для отдельных широт Земли авторами рассчитана инсоляция за 200 тыс. лет, предшествующие настоящей эпохе (1950 г.). Отличия результатов выполненных расчетов по оценке авторов не превышают 0,1% от результатов расчетов М. Миланковича, полученных для этого интервала [151]. Однако, следует отметить, что из-за использования упрощенного алгоритма авторами получены завышенные значения вековых колебаний наклона оси вращения (и связанных с этим значений инсоляции). Размах вековых колебаний угла наклона в работе [151] составляет около 18°. В расчетах Миланковича [114] выполненных на интервал в 600 000 лет в прошлое от эпохи 1800 г. угол наклона изменялся от 0,873° до – 1,538°. Размах колебаний, таким образом, составляет 2,411°. В расчетах выполненных Шараф и Будниковой [208, 209] на 30 млн. лет в прошлое размах колебаний составил 2,5°. В расчетах Ласкара с коллегами [314, 316] размах колебаний угла наклона составляет 2,379°. Кроме того, из небесной механики давно известно, что изменение угла наклона оси вращения ограничено пределом равным 2 градусам 37 минутам (или 2,617°) [196]. Таким образом, завышенные значения амплитуды колебаний наклона оси (и, связанных с этим колебаний инсоляции) являются результатом значительных упрощений в расчетном алгоритме и начальных данных. Оценочная характеристика сравнения с результатами Миланковича (0,1%) в связи с этим представляется сомнительной.

Следует отметить, что при приближенном аналитическом решении задач, связанных с орбитальным движением, вводятся упрощения физического и математического характера (например, взаимодействующие тела рассматриваются как материальные точки или тела определенной формы и т. д.). В связи с этим возможные ошибки при расчетах на большие периоды возрастают (поэтому М. Миланкович полагал, что надежные результаты могут быть получены на период 600 тыс. лет). Ш.Г. Шараф и Н.А. Будникова уточнили исходные данные и прецессионные решения, а также рассчитали инсоляцию на интервал 30 млн. лет. А. Берже и М. Лутр выполнили расчеты для интервала в 5 и 3 млн. лет [228, 229], Т. Кинн с коллегами рассчитали вариацию инсоляции на 3 млн. лет [340]. Ж. Ласкар и его коллеги усовершенствовали теорию вековых возмущений и выполнили расчеты изменения инсоляции за время до 200 млн. лет, но из-за проявления хаотичности в поведении основных характеристик пришли к выводу о том, что результаты можно считать достоверными только в пределах от 20 млн. лет в прошлом до 10 млн. лет в будущем [314, 316]. Эти методики, программы расчета [228–230] и данные инсоляции используются при численных экспериментах в палеоклиматическом моделировании.

В целом с историей развития астрономической теории климата связано получение серии расчетных значений вековых (низкочастотных) вариаций приходящей солнечной радиации (солярного климата Земли), связанных с вековыми вариациями элементов орбиты Земли (эксцентриситета, долготы перигелия) и наклона оси вращения. Количественные результаты этого решения – расчета вековых вариаций солнечной радиации – у различных исследователей несколько различаются в связи с различиями в начальных условиях и в способах расчетов (рис. 2.8.). Однозначного решения проблемы глобальных климатических изменений (развития оледенений) с позиций астрономической теории климата получено не было. Корреляционные поиски связи периодов экстремальных величин в приходе радиации с периодами максимального развития оледенений и межледниковыми периодами без учета влияния атмосферы, океана и других факторов на формирование глобального климата оказались неэффективными в отношении поисков причин его изменений [211, 309]. Осложняет объяснение развития оледенений вековыми изменениями солнечной радиации ряд иных явлений, например, метахронность оледенений [70, 109, 164, 176], отсутствие оледенений в течение длительных геологических периодов (например, меловой). Таким образом, в масштабах геологического времени решающее значение могут иметь иные, кроме приходящей на ВГА солнечной радиации, климатообразующие факторы. Например, скорость вращения Земли, движение полюсов и материков, рельеф и очертания материков и океанов, траектории океанических течений, состав атмосферы и характер атмосферной циркуляции, вулканическая активность и другие [24, 92, 95, 147, 149, 155, 156, 158, 166]. Вариации солярного климата представляются приоритетным фактором климатообразования при анализе климатических изменений на непродолжительных временных интервалах, на которых влияние многих из отмеченных факторов (например, движение материков, полюсов, изменение очертаний материков и океанов) можно не учитывать (или считать постоянным).

Временной диапазон исследований, относящихся к астрономической теории климата, определяется исследованием вековых (низкочастотных) вариаций солнечной радиации, что связано с основной задачей – объяснением глобальных климатических событий в геологических масштабах времени. В астрономической теории климата вековые вариации солнечной радиации рассчитываются в связи с вековыми возмущениями двух орбитальных элементов – эксцентриситета орбиты и долготы перигелия, а также наклона оси вращения. При этом считается, что «Возмущения бывают двух родов: периодические, происходящие в чрезвычайно узких пределах, и вековые. Первые не оказывают почти никакого влияния на облучение Земли и поэтому для нас не представляют интереса» [114, стр. 37]. Выполненные М. Миланковичем расчеты показывают, что «количества радиации, получаемые во время астрономической весны и лета, одинаковы так же, как и количества радиации, получаемые во время осени и зимы». Также из расчетов следует, что «любая широта южного полушария получает за свое летнее полугодие столько же радиации, сколько та же широта северного полушария в течение своего летнего полугодия; то же относится и к зимним полугодиям» [114, стр. 33]. При исследовании вековых вариаций принимается постоянство как большой полуоси земной орбиты (в соответствии с теоремой устойчивости Лапласа), так и продолжительность времени обращения Земли вокруг Солнца (по третьему закону Кеплера) [114]. Однако следует напомнить, что законы Кеплера справедливы для невозмущенного движения. Также следует отметить, что теорема устойчивости Лапласа справедлива только при отсутствии соизмеримостей в средних движениях больших планет [9, 48, 49]. Однако, в средних движениях Земли и ближайших планет – Марса, Венеры, а также Юпитера [39] – отмечаются соизмеримости (2/1, 3/5, 12/1 соответственно), или явление орбитального резонанса. В связи с этим постоянство большой полуоси земной орбиты и продолжительность периода ее обращения вокруг Солнца в реальности точно не соблюдается. С периодическими изменениями величины большой полуоси земной орбиты, продолжительности периода ее обращения вокруг Солнца и наклона оси вращения, вследствие орбитального резонанса, связаны малые периодические вариации солярного климата Земли [166, 173, 177, 185, 186, 188, 192, 258–263].

Все расчеты приходящей солнечной радиации, о которых речь шла выше, объединяет одно: они проводились в диапазоне низкочастотных вариаций. Как верно отмечалось Ж. Лагранжем, П. Лапласом и М. Миланковичем, периодические (высокочастотные) возмущения являются несущественными, по сравнению с вековыми (низкочастотными) возмущениями, при рассмотрении солярного климата Земли в масштабах геологического времени. Для интервала времени малой продолжительности (десятки – сотни лет) высокочастотные вариации солярного климата Земли могут иметь определенное значение среди прочих причин изменения современного глобального климата и погоды.

Таким образом, необходимость расчетов инсоляции Земли в диапазоне высокочастотных вариаций определяется несколькими причинами. Во-первых, это связано с постоянным обновлением исходных астрономических данных для расчетов инсоляции (учитывающим изменения в теории возмущений). Во-вторых, в связи с тем, что отклик климатической системы Земли во временном диапазоне вековых (низкочастотных) вариаций однозначно не определен, а в диапазоне периодических (высокочастотных) вариаций исследован совершенно недостаточно.

Исследования вариаций солярного климата Земли в диапазоне высокочастотных вариаций на современном временном интервале малой продолжительности представляются перспективными и по ряду других причин. Во-первых, этот интервал времени обеспечен астрономическими данными, обладающими наибольшей в настоящее время точностью. Во-вторых, он также обеспечен подробной климатологической информацией, что позволяет проводить детальные исследования связи вариаций климатических элементов с изменением поступающей к Земле солнечной радиации (определение термической, например, чувствительности климатической системы к вариациям инсоляции). Найденные связи могут использоваться при палеогеографических реконструкциях (по принципу известного в геологии метода актуализма) или моделировании палеоклимата. Этот временной масштаб удобен и для сравнительного анализа вариаций приходящей солнечной радиации разной физической природы (связанных с небесно-механическими процессами и активностью Солнца). Он представляет, таким образом, возможность для определения характера отклика климатической системы Земли на вариации приходящего потока солнечной радиации разной физической природы.

2.1.2. Высокочастотные изменения инсоляции

Расчеты, учитывающие периодические возмущения элементов земной орбиты и связанные с ними высокочастотные вариации солнечной радиации, были начаты в Главной геофизической обсерватории имени А.И. Воейкова, в России [233, 234]. Однако, дальнейшего развития эти исследования не получили. Исследования высокочастотных вариаций инсоляции также были начаты в институте астрономии и геофизики имени Г. Леметра, Бельгия [231, 322]. Позднее расчеты инсоляции (на основе точного решения задачи движения 2-х тел) в этом диапазоне проводились в Институте криосферы Земли (Тюмень) И.И. Смульским и О.И. Кротовым [151].

Расчеты инсоляции в диапазоне высокочастотных вариаций также были выполнены в МГУ имени М.В. Ломоносова автором совместно с А.А. Костиным [166, 297]. Расчеты приходящей солнечной радиации выполнялись нами по данным высокоточных астрономических эфемерид [274, 288] для всей поверхности Земли (без учета атмосферы) в интервале с 3000 г. до н.э. по 2999 г. н.э. Исходными астрономическими данными для расчетов инсоляции были склонение и эклиптическая долгота Солнца, расстояние от Земли до Солнца, разность хода равномерно текущего (среднего солнечного) и всемирного корректируемого времени (истинного солнечного). Поверхность Земли аппроксимировалась эллипсоидом (GRS80 – Geodetic Reference System, 1980) с длинами полуосей равными 6378137 м (большие) и 6356752 м (малая). В общем виде алгоритм расчетов можно представить выражением:

(2.2) $I_{nm} ({\phi }_1,{\phi }_2)={\int }_{t_1}^{t_2}\left({\int }_{{\phi }_1}^{{\phi }_2}\sigma \right(H,\phi \left)\right({\int }_{-\mathrm{\pi }}^{\mathrm{\pi }}\mathrm{\Lambda }(H,t,\phi ,\alpha )d\alpha )d\phi )dt,$

где I – приходящая солнечная радиация за элементарный n-й фрагмент m-го тропического года (Дж); σ – площадной множитель (м2), с помощью которого вычисляется площадной дифференциал σ(H,φ) dα dφ – площадь бесконечно малой трапеции – ячейки эллипсоида; α – часовой угол, φ – географическая широта, выраженные в радианах; H – высота поверхности эллипсоида относительно поверхности Земли (м); Ʌ(H, φ, t, α) – инсоляция в заданный момент в заданном месте поверхности эллипсоида (Вт/м2), t – время (с). Шаги при интегрировании составляли: по долготе 1°, по широте 1°, по времени 1/360 часть продолжительности тропического года [170]. Значение солнечной постоянной (среднее многолетнее значение TSI) принималось равным 1361 Вт/м2 [308]. Изменение активности Солнца не учитывалось [166].

Основные отличия нашего подхода (по времени, пространству и исходным данным) от известных (из астрономической теории климата) расчетов низкочастотных вариаций инсоляции заключаются в следующем.

1. М. Миланкович и его последователи рассчитывали инсоляцию Земли (без учета атмосферы) на длительные периоды времени (от нескольких сотен тысяч до миллионов лет) с учетом только ее вековых вариаций, связанных с изменением эксцентриситета, долготы перигелия и наклона оси вращения Земли (с периодами в несколько десятков тысяч лет). Разрешение по времени в расчетах составляло приблизительно от 5 000 лет в расчетах М. Миланковича [114], Ш. Шараф и Н. Будниковой [207–209], С.А. Монина [118] до 1000 лет в работах А. Вернекара [359], А. Берже [225, 226, 229; e-mail сообщение M.F. Loutre, 2016]. Миланкович и его последователи рассчитывали суточную и годовую инсоляцию на некоторый начальный год (например, 1850 или 1950 год). Затем совершался шаг (от 1000 до 5000 лет) в прошлое (или в будущее) и процедура расчетов (с учетом изменения эксцентриситета, долготы перигелия и наклона оси) повторялась. Периодические вариации инсоляции не учитывались (продолжительность тропического года принималась постоянной). В наших расчетах учитывались вековые и периодические вариации (расстояния Земля – Солнце, продолжительности тропического года, наклона оси вращения и т. д.). Разрешение по времени при интегрировании в наших расчетах составляло 1/360 часть продолжительности тропического года (приблизительно сутки) с учетом вариаций этой продолжительности.

2. М. Миланковичем и всеми его последователями расчеты выполнялись только для отдельных географических параллелей (широт), принималось, что Земля имеет форму сферы. В наших расчетах инсоляция рассчитывалась для всей земной поверхности, аппроксимируемой эллипсоидом (и отдельных широтных зон). Разрешение по пространству при интегрировании составляло по долготе 1°, по широте 1°.

3. Для выполнения расчетов М. Миланковичем (точнее В. Мишковичем) на длительный период были рассчитаны астрономические эфемериды для эксцентриситета, долготы перигелия и наклона оси вращения Земли, которые в дальнейшем уточнялись его последователями [207–209, 225, 226, 235, 237]. И.И. Смульский и О.И. Кротов [151] проводили расчеты на основе решения задачи 2-х тел (т.е. по существенно упрощенному алгоритму с рядом ограничений в исходных астрономических данных). Нами для расчетов инсоляции использовались приведенные в формуле (2.2) параметры, учитывающие вековые и периодические вариации элементов орбиты Земли и оси ее вращения. В качестве исходных данных для расчетов использовались высокоточные астрономические эфемериды, рассчитанные в Лаборатории реактивного движения Калифорнийского технологического института (период от 3000 лет до н.э. до 3000 лет н.э.) и размещенные на электронном ресурсе NASA [288].

Отличия нашего подхода в анализе высокочастотных вариаций инсоляции от методов Е.П. Борисенкова, M.-Ф. Лутр (Loutre), С. Бертрана (Bertrand) и их коллег связаны, во-первых, с исходными астрономическими данными, используемыми в расчетах. Во-вторых, с различным решением расчетов инсоляции относительно поверхности Земли. В-третьих, по временному интервалу, охваченному расчетами. В качестве исходных данных Борисенковым с коллегами использовались эфемериды, рассчитанные в Институте теоретической астрономии Академии наук СССР (e-mail сообщение А.В. Цветкова, 2015). Исходными данными для расчетов, выполненных бельгийскими исследователями (Loutre, et al., 1992; Bertrand et al., 2002), были эфемериды VSOP82 [235]. В наших расчетах использовались JPL (Jet Propulsion Laboratory) Planetary and Lunar Ephemerides DE–405/406 [288, 348].

Поверхность Земли при расчетах инсоляции отождествлялась нашими предшественниками со сферой, и расчеты выполнялись только для отдельных параллелей (широт). Е.П. Борисенковым с коллегами [233, 234] получены значения только для параллелей 20°, 40°, 60° и 80° северной широты. В исследованиях бельгийских ученых [322] расчеты выполнялись (на середину июля, точнее для точки с геоцентрической долготой равной 120°) только для параллели 65° северной широты, для точек равноденствия и солнцестояния – для экватора и параллелей 30°, 60° и 90° в каждом полушарии. Напомним, что геоцентрическая долгота Солнца это угол между направлением из центра Земли на точку весеннего равноденствия и Солнце. Точки весеннего и осеннего равноденствия – точки пересечения плоскости земной орбиты (эклиптики) с плоскостью небесного экватора [10, 11].

В работе С. Бертрана с коллегами [231] расчеты инсоляции охватывают предшествующее тысячелетие, они также относятся к июлю (точке с геоцентрической долготой равной 120°) и рассчитаны для широтной зоны 65°–70° с. ш. При этом значения для широтной зоны рассчитывались осреднением значений, полученных для ограничивающих широтную зону параллелей 65° и 70°. В работе И.И. Смульского и О.И. Кротова расчеты выполнялись для параллелей 0°, 10°, 25°, 45°, 65°, 80° и 90 ° каждого полушария. В наших расчетах поверхность Земли аппроксимировалась эллипсоидом, и приходящая радиация рассчитывалась не на отдельные параллели (широты), а на поверхность отдельных широтных зон (с разрешением по широте в 1°) и всей Земли.

Разрешение по времени при расчетах высокочастотных вариаций инсоляции в работе Е.П. Борисенкова с коллегами приблизительно соответствуют суткам (Borisenkov et al., 1983). Однако выполненные ими расчеты представлены только для зимнего и летнего полугодий (и только для северного полушария) в интервале с 1800 по 2100 гг. В работе M.F. Loutre с коллегами [322] расчеты проводились на интервале в 5000 лет (в прошлое) с годовым разрешением и только для июля (отдельной точки с геоцентрической долготой 120°), точек равноденствия и солнцестояния. В работе C. Бертрана с коллегами [231] расчеты инсоляции охватывают предшествующее тысячелетие, но они относятся только к одному месяцу – июлю (выполнены с годовым разрешением). Кроме этого, значение солнечной постоянной в наших расчетах принималось равным 1361 Вт/м2 [308]. В работах наших предшественников – 1368 Вт/м2 [232], 1367 Вт/м2 в работах Е.П. Борисенкова с коллегами (e-mail сообщение А.В. Цветкова, 2015) и М.F. Loutre с коллегами [322], 1366 Вт/м2 [230]. И.И. Смульский и О.И. Кротов [151] использовали тоже значение солнечной постоянной, что и М. Миланкович – 1395,6 Вт/м2.

Наши расчеты основаны на высокоточных эфемеридах, в них используется новое значение солнечной постоянной (1361 Вт/м2), более детально охватывается временной интервал протяженностью в 5999 лет и вся поверхность Земли. Земля в наших расчетах не отождествляется со сферой, а аппроксимируется эллипсоидом. Выполненные расчеты, таким образом, закрывают пространственные и временные «бреши» в расчетах инсоляции для периода от 3000 лет до н.э. до 2999 лет н.э., что создает возможности для детального анализа инсоляции Земли, изменения ее солярного климата в отмеченном интервале времени.

По результатам расчетов сформирована общедоступная база данных приходящей солнечной энергии во все широтные зоны Земли (протяженностью в 5 градусов) за каждый астрономический месяц каждого года для периода от 3000 лет до н.э. до 2999 лет н.э. [297]. Значения инсоляции Земли, представленные в массивах данных (в трех единицах измерения – Дж, Дж/м2 и Вт/м2), используются при дальнейшем анализе в данной работе. Размерность соответствует общей лучистой энергии, удельной энергии и ее интенсивности. Эта база отражает вариации солнечной радиации иной физической природы, чем вариации, которым посвящен первый раздел главы. Они также могли бы использоваться как входной энергетический сигнал в радиационном блоке новых физико-математических моделей климата (Incoming Solar Radiation). Рассчитанные нами данные по инсоляции могут использоваться и при точных расчетах радиационного баланса Земли, поскольку верхняя граница атмосферы (ВГА) является условной поверхностью отсчета приходящей к Земле лучистой энергии (рис.2.9) [18, 280, 284, 355–357].

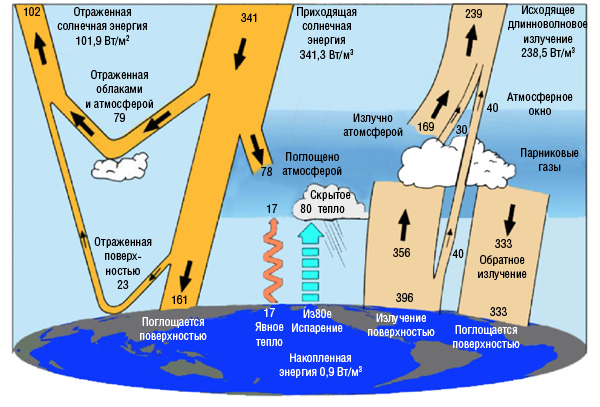
Рис. 2.9. Составляющие радиационного баланса Земли [357]

Значение 341 Вт/м2 на входе (на внешней границе атмосферы или на поверхности Земли без учета атмосферы) получается делением значения солнечной постоянной (для рис. 1.9–1364 Вт/м2) на 4, так как солнечная постоянная – это лучистая энергия, приходящая на единицу площади диска Земли (при расстоянии в 1 а.е). Площадь же сферы в 4 раза больше площади ее большого круга. В наших базах данных входной радиационный сигнал рассчитан не относительно площади сферы, а относительно площади эллипсоида [297].

Таким образом, при изучении вариаций TSI (Total solar irradiance) отсчет ведется относительно неизменного расстояния между Солнцем и Землей равного 1 а.е. (среднее за год). При расчетах вариаций инсоляции, связанных с небесно-механическими процессами, расчеты проводятся от принятого и неизменного значения солнечной постоянной (среднего многолетнего значения TSI и не нормируются по расстоянию). В главах 4–6 будет показано, что для объяснения современных изменений климата наиболее значимыми являются изменения инсоляции по широтам и сезонам связанные с изменением наклона оси вращения Земли в результате прецессии и нутации.