1.1. Законы орбитального движения планет
1.1.1. Закон Ньютона и небесная механика
1.1.5. Синхронизация, соизмеримости и резонанс
1.2. Законы теплового излучения
1.2.2. Распространение излучения
***
1.1. Законы орбитального движения планет
Поступление солнечной радиации к Земле связано с небесно – механическими процессами изменяющими элементы орбиты Земли, которыми определяется ее орбитальное движение. В связи с этим в разделе приводится краткое изложение, во-первых, законов, по которым происходит движение небесных тел и, во-вторых, – законов, которыми определяется солнечное излучение (законы теплового излучения).
Орбитальные движения небесных тел изучаются небесной механикой – одним из разделов астрономии. Основные законы, которыми определяется орбитальное движение – это закон всемирного тяготения Ньютона и три закона Кеплера.
1.1.1. Закон Ньютона и небесная механика
Основу теории притяжения составляет закон всемирного тяготения И. Ньютона, сформулированный им в «Математических началах натуральной философии» (1687 г.) и признающийся одним из основных законов природы [48, 123, 138, 150, 212].
Согласно этому закону всякие две материальные частицы взаимно притягиваются с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
где f – коэффициент пропорциональности, называемый постоянной притяжения (или постоянной тяготения или гравитационной постоянной).
Материальная частица – понятие физическое, под которым подразумевается весьма малое количество какого-либо вещества в любом физическом состоянии: газообразном, жидком или твердом, занимающее весьма малый объем. Уточнение этого несколько неопределенного понятия, позволяет определить механическое понимание материальной точки, как геометрической точки пространства, т.е. объекта, не имеющего измерений, но обладающего конечной массой.
Первоначально закон Ньютона относился к материальным частицам, но в дальнейшем он был распространен на все тела непрерывной протяженности (состоящие из неограниченного числа материальных частиц). Было доказано, что два тела, обладающие любой формой и произвольным внутренним строением, взаимно притягиваются с силой, почти обратно пропорциональной квадрату расстояния между их центрами масс, если линейные размеры тел малы по сравнению с этим расстоянием. Отдельно было доказано, что два шара, обладающие сферической структурой, взаимно притягиваются с силой пропорциональной их массам и обратно пропорциональной квадрату расстояния между их центрами. Звезды, планеты и их спутники имеют близкую к шарообразной форму и расстояния между этими небесными телами весьма велики. На основе приведенных результатов теории притяжения можно с достаточным основанием считать, что такие небесные тела взаимно притягиваются друг к другу так же, как притягивались бы материальные точки, помещенные в центрах инерции этих тел и обладающие их массами [48, 55–57, 85, 86, 140, 144–146, 198].
Известно, что всякое движение происходит вследствие совместного действия ряда сил. Исследование движения требует знания характера этих сил и законов, определяющих их изменения. Если это известно, то изучение или исследование движения в небесной механике сводится к составлению дифференциальных уравнений движения и к последующему исследованию этих уравнений и их интегралов [47, 48].
Силы, обуславливающие движения небесных тел различаются по своему характеру и происхождению. Законы, определяющие их изменение, в некоторых случаях известны только весьма приблизительно, а в других случаях и совершенно неизвестны, вследствие чего изучение движений с абсолютной точностью и во всех подробностях становится фактически невозможным. Поэтому, при изучении движения небесных тел возникает необходимость отказываться от решения очевидно безнадежной задачи и заменять ее другой или другими, более простыми задачами. Таким образом, приходится ограничиваться приближенным и последовательным исследованием движения небесных тел. Такой подход получил название метода последовательных приближений, основная идея которого состоит в замене основной, весьма сложной задачи, рядом более простых (но с каждым последующим шагом все более усложняющихся) задач [47, 48]. Следуя этому методу, небесная механика сосредотачивает свое внимание, прежде всего, на силе притяжения, происхождение и природа которой до сих пор неизвестна, но наличие, которой было установлено Ньютоном в законе всемирного тяготения. Основной задачей небесной механики, таким образом, является «изучение движения материальной системы, состоящей из конечного числа свободных материальных точек, обладающих постоянными массами и движущихся в абсолютно пустом пространстве под действием сил взаимных притяжений, определяемых законом всемирного тяготения Ньютона» [48].
Движение планеты будет вполне определено, если известны плоскость, в которой лежит ее орбита, размеры и форма этой орбиты, ее ориентировка в плоскости и момент времени, в который планета находится в определенной точке орбиты. Величины, определяющие орбиту планеты, называются элементами ее орбиты. За основную плоскость, относительно которой определяется положение орбиты, принимается плоскость эклиптики [10, 11, 48, 123, 138, 150, 212].
Эллиптическую орбиту планеты (при определении орбиты обычно используется триэдр – система трех взаимно перпендикулярных единичных векторов, выходящих из одной точки, сопоставляемой с центром притяжения планеты) определяют следующие 6 элементов:
1. Линия пересечения плоскости орбиты с плоскостью эклиптики (основная плоскость) – называется в астрономии линией узлов, а точки ее пересечения называются узлами орбиты. Узел орбиты, который движущаяся точка проходит, переходя из области отрицательных аппликат в область положительных, называется восходящим узлом, а противоположный – нисходящим узлом. Угол прецессии триэдра есть угол между направлением на восходящий узел и точку весеннего равноденствия. В астрономии этот угол называется долготой восходящего узла (или просто долготой узла) и обозначается Ω.
2. Угол собственного вращения триэдра есть угол между направлением на восходящий узел и направлением на перицентр (перигелий). Этот угол обычно обозначается ω и называется угловым расстоянием перицентра от узла (аргумент перигелия).
3. Угол нутации триэдра есть угол, который плоскость орбиты образует с основной плоскостью и поэтому называется наклонением или наклонностью орбиты и обозначается обыкновенно буквой i (для Земли i = 0).
Наклонение и долгота восходящего узла определяют положение плоскости орбиты в пространстве. Угловое расстояние перицентра от узла определяет положение орбиты в ее плоскости. Все три угла определяют, таким образом, положение плоскости орбиты в пространстве и положение линии апсид на этой плоскости, т.е. определяют расположение, или ориентацию орбиты. Каждый из них измеряется обычным образом в радианах, или в градусах, минутах и секундах дуги. Долгота восходящего узла Ω отсчитывается от точки весеннего равноденствия в сторону движения планеты от 0° до 360°. Угловое расстояние перицентра от восходящего узла отсчитывается в плоскости орбиты также в сторону движения точки (планеты) от 0° до 360°. Наклонение отсчитывается от 0° до 180°.
4. Большая полуось эллиптической орбиты или половина фокальной хорды, перпендикулярной к фокальной оси (a). Большая полуось эллиптической орбиты однозначно определяет сидерический период обращения T планеты. Часто одновременно с ней дается в качестве элемента среднее суточное движение , т.е. средняя угловая скорость планеты за сутки.
5. Эксцентриситет орбиты (е)
где p и q – полуоси эллиптической орбиты.
6. Момент прохождения через перицентр или, для Земли – перигелий (τ).
Пространственные координаты (прямоугольные декартовы, полярные сферические, цилиндрические и т.д.) x, y, z представляются формулами как функции времени t и шести произвольных постоянных
Эти постоянные называются элементами кеплеровской орбиты, кеплеровскими элементами невозмущенной орбиты или, иногда просто элементами орбиты (рис. 1.1, табл. 1.1). Они используются при решении задач небесной механики в различных формульных модификациях – преобразования Якоби, Делоне, Пуанкаре [48, 135, 138, 142].
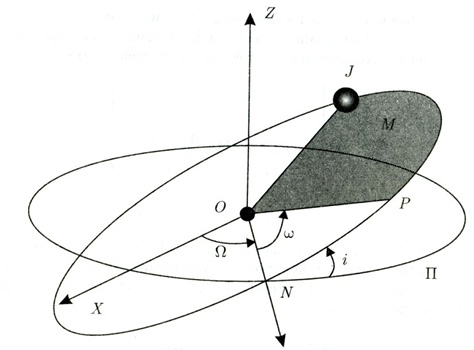
Рис. 1.1. Элементы эллиптической орбиты [89]
В любое заданное время можно рассмотреть планету (J), движущуюся по эллиптической орбите с большой полуосью (a) и эксцентриситетом (e), с Солнцем в одном фокусе (О). Ориентация этого эллипса по отношению к фиксированной плоскости П и направлением ординаты OX задается тремя углами: наклонением i, долготой узла Ω и долготой перигелия ῶ = Ω + ω, где ω – аргумент перигелия (Р). Положение планеты на эллиптической орбите задается средней долготой λ = М + ῶ, где М (средняя аномалия) – угол, пропорциональный площади OPJ (третий закон Кеплера).
Таким образом, элементы орбиты условно разделяются на три группы. К первой группе относятся элементы Ω, i, ω, определяющие положение плоскости орбиты в пространстве и положение орбиты в ее плоскости. Вторую группу составляют элементы a, e, определяющие размеры орбиты и ее форму.
Третья группа включает элемент τ, определяющий положение планеты на орбите в некоторый начальный момент.
Элементы первой и второй групп это чисто геометрические величины, связанные с двумя основными векторами – вектором момента количества движения и вектором Лапласа (совпадающим с линией апсид). При этом элементы первой группы определяют направления этих векторов, а элементы второй группы связаны с их модулями. Так как элемент третьей группы τ связан с движением по орбите то он также иногда называется динамическим элементом. Вместо τ иногда используются и другие, зависящие от него величины, например, истинная аномалия в начальный момент (или, как принято в астрономии, истинная аномалия эпохи). Истинная аномалия v0 угол между направлением на точку (планету) и направлением на перицентр (перигелий). Угол отсчитывается от перицентра в положительном направлении (против часовой стрелки) от 0° до 360° или до 180°.
Таблица 1.1
Элементы орбит планет в эпоху J2000 [124].
В графе «Земля» приведены данные для барицентра Земля – Луна;
для указаны значения средней долготы перигелия
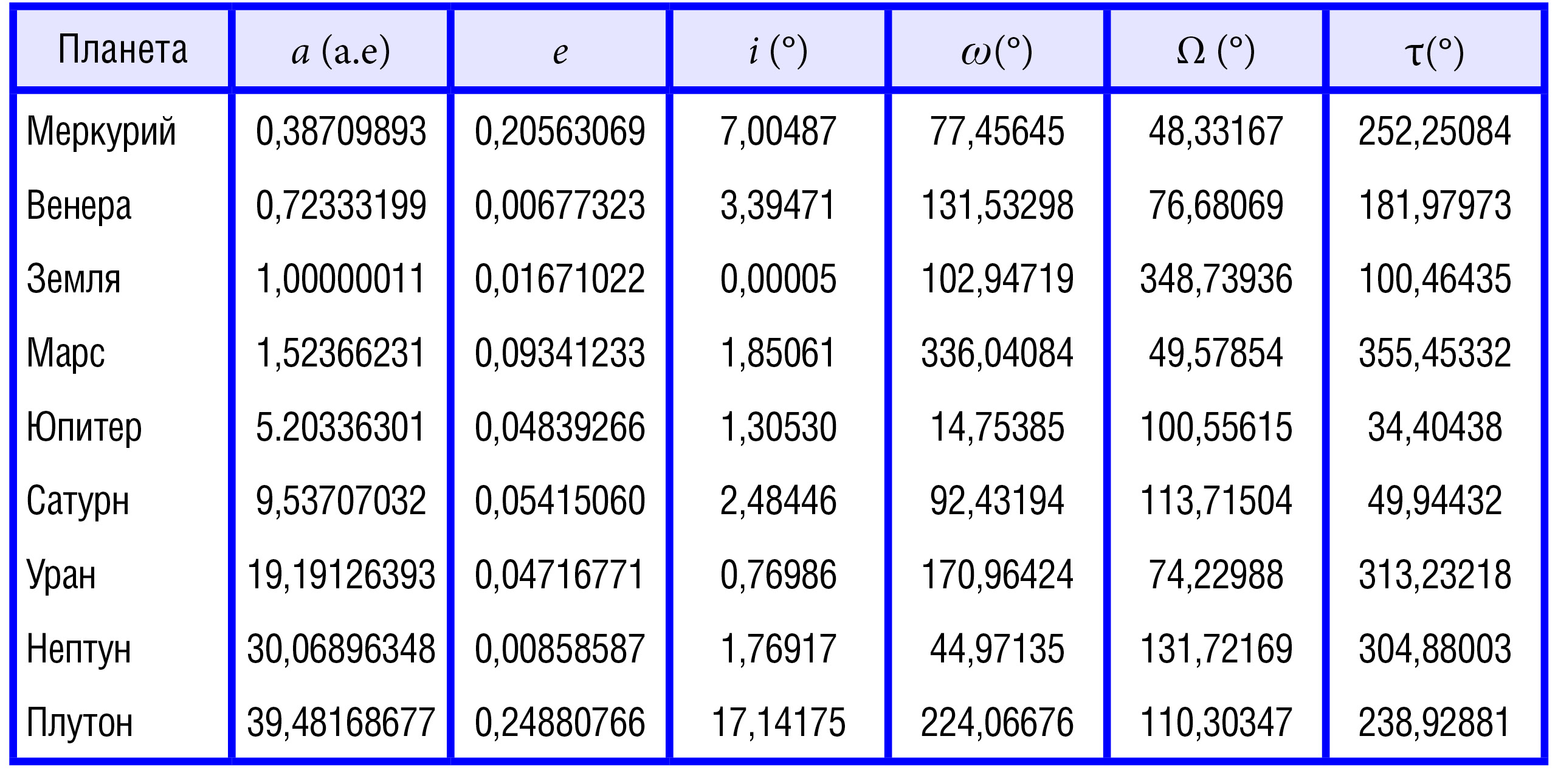
Как следует из законов Кеплера невозмущенная орбита движущейся планеты, представляет собой плоскую кривую второго порядка, один из фокусов которой находится в начале координат (в центре силы притяжения) и главная, или фокальная, ось которой совпадает с направлением вектора Лапласа. Эта ось называется в астрономии линией апсид; точки пересечения ее с кривой называются абсидами. Апсиды совпадают с вершинами кривой второго порядка, которая представляет орбиту, и имеют собственные названия. В общем случае точка орбиты, ближайшая к центру силы, называется перицентром, а наиболее удаленная – апоцентром. В конкретных задачах астрономии апсиды орбиты имеют свои собственные названия. Так, если рассматривается движение планеты вокруг Солнца, то перицентр называется перигелием, а апоцентр – афелием. Если рассматривается движение Луны вокруг Земли, то перицентр называется перигеем, а апоцентр – апогеем [11, 48, 68, 138, 150, 153].
В общем решении системы дифференциальных уравнений (общий интеграл) невозмущенного кеплеровского движения содержится необходимое число (шесть) произвольных постоянных (элементов орбиты), определяемых произвольно задаваемыми начальными значениями координат и составляющих скорости движущейся планеты. Однако при различных начальных условиях одно и то же невозмущенное движение обладает, в общем случае, различными свойствами. Так, например, вид и геометрические свойства орбит существенно зависят от начальных условий, а от вида орбиты зависит функциональная связь между истинной аномалией и временем. С другой стороны, от характера этой функциональной связи зависит последовательность формул, используемых для вычисления эфемерид, т.е. для определения места небесного тела в пространстве в заданное время.
Невозмущенное движение определяется тремя законами Кеплера [11, 48, 68, 110, 123, 138, 139, 150, 153, 212].
1. Первый (обобщенный) закон Кеплера (обобщенный потому, что первоначально он был выведен для эллиптической орбиты, но эллипс – это частный случай кривой второго порядка): в невозмущенном движении орбита движущейся точки есть кривая второго порядка, в одном из фокусов которой находится центр силы притяжения.
2. Второй (обобщенный) закон Кеплера: в невозмущенном движении площадь, описываемая радиусом – вектором движущейся точки, изменяется пропорционально времени. Второй закон Кеплера, устанавливающий неизменность секториальной скорости, также был выведен для случая эллиптической орбиты планеты в ее движении вокруг Солнца, но, как и первый, распространяется на случай любой кеплеровской орбиты (эллипса, параболы, гиперболы).
Из общей астрономии известен третий закон Кеплера, устанавливающий связь между средним расстоянием планеты от Солнца и временем ее обращения вокруг Солнца. Этот закон имеет место только для случая эллиптического движения.
3. Третий закон Кеплера: квадраты времен обращения планет пропорциональны кубам их средних расстояний от Солнца (больших полуосей их орбит).
Третий закон Кеплера записывается так:
где T1и T2 – сидерические периоды обращений планет, a1 и a2 – большие полуоси их орбит (в небесной механике и общей астрономии буквенные обозначения иногда отличаются). Если большие полуоси орбит планет выражаются в единицах среднего расстояния Земли от Солнца (в астрономических единицах), а периоды обращений планет – в годах, то для Земли a = 1 и T = 1 , период обращения вокруг Солнца любой планеты
Первые два закона Кеплера в их полной формулировке имеют место только для невозмущенного движения, происходящего под действием силы притяжения, обратно пропорциональной квадрату расстояния до центра силы. Поэтому невозмущенное движение в этом случае и называется часто кеплеровским движением.
Уравнение эллиптической орбиты в полярных координатах имеет вид:
где p – параметр кривой, определяющий размеры орбиты, e – ее эксцентриситет, v – истинная аномалия.
Если 0 ≤ e ≤ 1, то орбита представляет собой эллипс, и движение точки называется в этом случае эллиптическим кеплеровским движением. Если e = 0, то эллипс вырождается в окружность (и движение называется круговым). Если 1 < e < ∞, то орбита представляет собой гиперболу (точнее ее ветвь, внутри которой находится центр силы) и движение точки называется гиперболическим кеплеровским движением. В предельном случае при e = 1 орбита точки выражается параболой; в этом случае движение точки называется параболическим кеплеровским движением [48].
Основная сила, управляющая движением тел Солнечной системы – притяжение Солнца. Однако, если бы тела Солнечной системы притягивались только Солнцем, то они двигались бы вокруг Солнца точно по законам Кеплера. Такое движение, как уже отмечалось, называется невозмущенным (кеплеровским). В действительности же все тела Солнечной системы притягиваются не только Солнцем, но и друг другом. Поэтому ни одно тело в Солнечной системе не может двигаться точно по эллипсу, параболе, гиперболе или по кругу. Отклонения в движении тел от законов Кеплера называются возмущениями, а реальное движение тел – возмущенным (лагранжевым) движением. Орбиты планет не являются неподвижными инвариантными эллипсами. Изменение элементов орбиты планеты вследствие ее притяжения другими телами, помимо центрального, называют возмущениями (или неравенствами элементов). Вызывающая эти возмущения возмущающая сила – это геометрическая разность действий возмущающего тела на планету и на Солнце. Возмущающие силы претерпевают значительные изменения по величине и направлению вследствие изменений направлений и расстояний между возмущающими планетами, но возмущающие силы, в общем, малы по сравнению с притяжением Солнца. Наибольшая возмущающая сила, действующая на Землю, это притяжение Юпитера, которое составляет всего примерно 5 × 10–5 притяжения Солнца [11, 48, 123, 131, 138].
Основной метод исследования возмущенного движения в небесной механике – метод изменения (или вариации) произвольных постоянных Лагранжа («Théorie des variations séculaires des éléments des planèts», 1782). Суть этого метода в том, что решение уравнений возмущенного движения определяется теми же формулами, что и решение уравнений невозмущенного движения, но величины Ω, i, ω, a, e, τ рассматриваются в этих формулах не как постоянные, а как некоторые функции времени, определяемые так, чтобы уравнения возмущенного движения строго удовлетворялись. С математической точки зрения осуществление идеи Лагранжа сводится просто к преобразованию переменных, причем формулами преобразования служат формулы невозмущенного движения. Уравнения, определяющие изменения оскулирующих элементов Ω, i, ω, a, e, τ при произвольно заданной возмущающей силе, приводятся в том или ином виде во всех классических работах и в большинстве современных курсов по небесной механике [12, 48, 135, 138, 210, 212].
Изменяя время t непрерывным образом начиная с начального момента t0, можно получить бесчисленное множество невозмущенных движений, отличных друг от друга, и единственное возмущенное движение, состояние которого совпадает в каждый момент времени с состоянием соответствующего невозмущенного движения (рис. 1.2). Так как траектория возмущенного движения в каждый момент соприкасается с траекторией соответствующего невозмущенного движения то, по сути, траектория возмущенного движения, есть огибающая семейства траекторий невозмущенных движений. Все эти траектории невозмущенного движения отличны друг от друга, но они имеют и нечто общее. Действительно, любая траектория семейства есть в общем случае кривая второго порядка (эллипс, парабола или гипербола), один из фокусов которой находится в начале координат, и движение по которой совершается в соответствие с законами Кеплера. В астрономии соприкасающиеся кривые называются оскулирующими, а отмеченные выше траектории семейства невозмущенных движений называются оскулирующими орбитами, а их элементы – оскулирующими («oskulatio» – лат. – «поцелуй») элементами [48, 123, 210, 212].
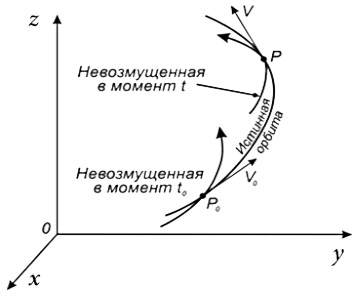
Рис. 1.2. Траектории кеплеровского невозмущенного движения
и оскулирующая орбита возмущенного движения [48]
Таким образом, в методе Лагранжа истинное (возмущенное) движение рассматривается как постоянно и непрерывно изменяющееся кеплеровское движение, а истинная орбита – как постоянно и непрерывно изменяющаяся оскулирующая орбита. Отсюда и следует возможность использования формул невозмущенного движения для расчетов возмущенного движения при рассмотрении элементов орбиты (и величин зависящих от них) в качестве некоторых непрерывных функций времени [48, 123].
Решение дифференциальных уравнений определяющих кеплеровские элементы оскулирующей орбиты движущейся точки (тела) позволяют методом последовательных приближений (итераций) получить возмущения первого, второго, третьего и более высоких порядков (до бесконечности). На практике пользуются большей частью одним только первым приближением, иногда вторым, и очень редко третьим. Это объясняется не только громоздкостью выкладок, сложность которых быстро растет по мере увеличения числа приближений, но также и тем, что в большинстве конкретных случаев уже одно первое приближение дает результаты достаточно близкие к действительности [48].
Решение уравнений показывает, что возмущение первого порядка элемента орбиты состоит из трех аналитически различных частей. Первая из этих частей есть величина постоянная, зависящая от начальных значений элементов; ее называют постоянной частью возмущения первого порядка. Вторая часть состоит из одного члена, который медленно и монотонно возрастает по числовой величине вместе со временем; его называют вековой частью возмущения первого порядка или, короче, вековым неравенством. Третья часть состоит из бесчисленного множества тригонометрических членов и является периодической функцией от времени; она называется периодической частью возмущения первого порядка, или просто периодическим возмущением. Члены этого периодического возмущения являются периодическими функциями времени и называются периодическими неравенствами. Таким образом, возмущение первого порядка каждого элемента эллиптической орбиты состоит из постоянного неравенства, векового неравенства и бесчисленного множества периодических неравенств [48, 212].
Периодические неравенства разделяют на две группы в зависимости от величины периода: короткопериодические неравенства (период которых сравним с периодом обращения 2π/ω и долгопериодические неравенства (они играют значительную роль в теории возмущений, особенно когда рассматриваются большие промежутки времени).
При практических применениях теории возмущений невозможно вычислить бесчисленное множество членов, образующих возмущения даже первого порядка. Поэтому из всего бесчисленного множества неравенств рассматриваются только некоторые, а возмущение первого порядка каждого элемента представляются в виде суммы векового неравенства и нескольких периодических, амплитуды которых проявляются более значимо.
Относительно вековых неравенств в возмущениях первого порядка элементов оскулирующих орбит движущихся материальных точек Лапласом были определены условия, при которых возмущение первого порядка представлено только периодическими членами. Это свойство возмущений первого порядка впервые было замечено Лапласом для больших планет Солнечной системы (но имеет более общее значение) и называется обычно теоремой Лапласа, хотя в общем виде оно установлено Лагранжем [48]. Ее можно сформулировать так: если начальные средние движения двух точек несоизмеримы между собой, то возмущения первого порядка больших полуосей оскулирующих орбит точек, не содержат вековых членов (т.е. состоят только из периодической части). Лагранж показал, что если отбросить в решении все периодические члены и оставить только вековые возмущения оскулирующих элементов первого порядка, то их можно рассматривать сами по себе, а их интегрирование как самостоятельную задачу, результаты которой можно назвать теорией вековых возмущений оскулирующих элементов.
Из теоремы Лапласа в первом приближении следует, что полуоси оскулирующих орбит больших планет в их относительном движении вокруг Солнца можно считать свободными от вековых возмущений. Поэтому (в рамках первого приближения) считается, что большие полуоси испытывают только малые периодические колебания около их невозмущенных постоянных значений, из чего следует (с той же точностью приближения), что большие планеты постоянно обращаются вокруг Солнца на почти неизменных расстояниях с почти неизменными угловыми скоростями [48, 210]. Однако, в настоящее время, не известно обладают ли большие планеты этим свойством в действительности, но если допустить, что это действительно так, то в небесной механике почти строго доказывается, что общее устройство Солнечной системы будет всегда оставаться неизменным и таким же, каким оно является в настоящее время. Это утверждение составляет знаменитую теорему Лапласа об устойчивости Солнечной системы, хотя она как следует из изложенного, имеет только условное значение. Так, например, отмечается, что доказательство устойчивости Лапласа теряет свою силу для малых планет, наклонности и эксцентриситеты которых могут принимать большие значения [210].
Теорема Лапласа об устойчивости Солнечной системы имеет большое значение для небесной механики. Действительно, в настоящее время эксцентриситеты и наклонности орбит к плоскости эклиптики всех больших планет весьма малы. С другой стороны, вследствие отсутствия вековых неравенств в возмущениях первого порядка больших полуосей, величины больших полуосей для всех больших планет будут оставаться близкими (по крайне мере в течение двух – трех столетий) к их начальным (полученным из наблюдений) значениям. Поэтому можно утверждать, что в течение того же промежутка времени эксцентриситеты и наклонности орбит больших планет Солнечной системы действительно будут оставаться малыми [48].
Иными словами, в настоящее время орбиты девяти больших планет близки к круговым орбитам и лежат почти в одной плоскости. По теореме Лапласа следует, что такое устройство Солнечной системы будет сохраняться все время, пока большие полуоси будут оставаться близкими к их начальным значениям. Однако, распространять этот вывод на очень большие (космогонические) промежутки времени нет никаких оснований, вследствие чего устройство Солнечной системы в далеком будущем (а также в далеком прошлом), по существу остается неизвестным [48, 49, 138]. Следует, вероятно, учитывать и то, что отсутствие соизмеримостей в средних движениях в Солнечной системе скорее исключение, чем правило.
1.1.5. Синхронизация,
соизмеримости и резонанс
Синхронизация определяется, как «свойство материальных объектов самой различной природы вырабатывать единый ритм совместного существования, несмотря на различие индивидуальных ритмов и на подчас крайне слабые взаимные связи» [14]. Явление синхронизации состоит в том, что несколько, например, природных объектов, совершающих при отсутствии взаимодействия колебательные или вращательные движения с различными частотами (угловыми скоростями), при наложении даже весьма слабых связей начинают двигаться с одинаковыми, кратными или находящимися в рациональных отношениях частотами (угловыми скоростями). Причем, устанавливаются определенные фазовые соотношения между колебаниями и вращениями.
Орбитальное движение небесных тел представляет собой колебательные процессы, следовательно, в этих колебательных процессах могут проявляться явления и эффекты синхронизации (взаимная синхронизация), самосинхронизации, вырожденной синхронизации. Явление захватывания (вырожденная синхронизация, гармоническое захватывание) заключается в том, что при определенных условиях автоколебательная система, на которую действует внешняя возмущающая сила периода T0, совершает устойчивые колебания с периодом T = p / q T0, где p и q – целые положительные числа [5, 62, 107, 108, 201, 358].
Если представить, что имеется некоторое число k автоколебательных объектов, которые при отсутствии взаимных связей могут совершать движения с некоторыми индивидуальными частотами (угловыми или линейными скоростями) ωs; величины ωs называются парциальными частотами (скоростями) объектов. После установления связей между объектами, эти объекты будут совершать движения с одинаковой частотой (скоростью) ω или же с частотами (скоростями) вида ns ω, где ns – взаимно простые положительные числа. Соответствующие движения называются синхронными, причем в случае, когда все ns = 1 – это простая синхронизация, а в случае, когда встречаются ns ≠ 1, – кратная синхронизации [14].
К основным закономерностям синхронизации относятся следующие:
- Основной особенностью обнаруживаемой при исследовании синхронизации динамических систем, является отсутствие нижнего предела синхронизации. Синхронизация может иметь место при неограниченно слабой связи между объектами, если только достаточно мало отличие соответствующих одноименных параметров объектов. Иными словами, как бы слабо не были связаны между собой объекты, всегда существуют определенные условия, при которых их взаимное влияние приведет к качественному эффекту, который может быть зафиксирован – к установлению синхронизации.
- Наиболее существенно возможность или невозможность синхронизации автоколебательных объектов зависит от значений их парциальных частот (угловых скоростей) ωs. Если, например, все парциальные частоты достаточно близки или одинаковы, то простая взаимная синхронизация объектов, возможна всегда, вне зависимости от значений прочих параметров объектов и системы связи. Вместе с тем даже при слабых взаимных связях между объектами их тенденция к синхронизации может быть столь сильна, что синхронизируются объекты с существенно различными частотами. [14, 201].
- Синхронная частота (угловая скорость) ω при простой взаимной синхронизации автоколебательных объектов обычно не больше, чем наибольшая, и не меньше, чем наименьшая из парциальных частот (угловых скоростей) ωs отдельных объектов.
- В связанной системе объектов во многих случаях возможно не одно, а несколько устойчивых синхронных движений, отличающихся, например, фазами движения объектов.
- Характер и число устойчивых синхронных движений системы существенно зависят от числа степеней свободы и характера системы связи, а также от характера и числа объектов в системе [14].
Явление синхронизации – это механический процесс, возникающий и при движении небесных тел в Солнечной системе и приводящий к появлению соизмеримости в средних движениях планет и резонансам, а также к возникновению проблемы малых знаменателей в небесной механике. Это наиболее характерно для соседних планет, находящихся в тесном и постоянном гравитационном взаимодействии, имеющим периодическую структуру [12, 138, 163]. Классический пример синхронизации – резонанс в системе Земля – Луна. Периоды обращения Луны вокруг Земли и вокруг собственной оси примерно совпадают (порядок резонанса 1:1). Подобный резонанс называется синхронностью. Синхронная орбита – это траектория на которой орбитальный период спутника равен периоду вращения планеты. Это явление отмечается и для спутника Марса – Фобоса. В общем, согласно третьему закону Кеплера, если скорость движения спутника по орбите больше скорости вращения планеты, то спутник приближается, если меньше, то удаляется. Поэтому наличие синхронности свидетельствует о стабильности и определенном равновесии гравитационных сил в системе [10, 11]. Явление резонанса в Солнечной системе – это эффект гравитационного взаимодействия, во многом определяющий динамическую структуру Солнечной системы. Существует предположение о том, что эволюционными процессами в Солнечной системе управляют диссипативные (приливные) силы, и именно им обязаны происхождением некоторые из этих резонансов [34, 42, 100, 124, 134, 277–279, 249, 250, 325–327, 342].
Резонанс может возникать, когда существует простое численное соотношение между частотами или периодами средних движений (отношение частот или периодов равно рациональному числу). Такими периодами могут быть вращательный и орбитальный периоды одного объекта, в случае спин – орбитального взаимодействия, или же, например, орбитальные периоды двух или более тел, в случае орбитального взаимодействия.
Движения планет (их координаты и скорости) имеют весьма сложный характер и математически, могут быть представлены в виде кратных рядов Фурье, т.е. в виде комбинаций многих (или бесконечного множества) периодических движений с разными периодами (или частотами). Обычно при этом выделяются основные или главные частоты, которые по сравнению с другими есть большие величины. Например, в двухпланетной задаче (Солнце – планета – планета) можно выделить две основные частоты, соответствующие средним периодам обращения планет вокруг Солнца и представляющие собой средние движения по гелиоцентрическим орбитам. Эти основные частоты в астрономии называют средними движениями [38]. Средние движения планет не являются постоянными, но как показывают наблюдения, изменяются очень медленно, то есть являются медленными функциями времени. Значения средних движений относятся к некоторому определенному интервалу времени (эпохе).
Если в некоторой двухпланетной задаче основные частоты находятся в близкой соизмеримости, то возникает проблема малых знаменателей. Математически эффект малых знаменателей проявляется в том, что в решениях уравнений движения планет, представляемых рядами Фурье, появляются периодические члены с коэффициентами, знаменатели которых близки к нулю, т.е. появляются периодические гармоники с большими амплитудами. В движениях планет появляются эффекты, называемые в физике резонансными (наподобие резонансных колебаний двух маятников, точки подвеса которых находятся на общем горизонтальном стержне).
В Солнечной системе наблюдается много резонансных движений, определены резонансные соотношения между средними движениями (частотами) многих планет и спутников, между их вращательными и орбитальными движениями [138]. Наиболее очевидный пример спин – орбитального резонанса – это Луна, орбитальный период которой равен периоду ее вращения. Большинство крупных естественных спутников в Солнечной системе находятся в синхронном спин – орбитальном резонансе 1:1. Однако возможны и другие спин – орбитальные состояния. Например, Меркурий находится в спин – орбитальном резонансе 3:2. Отмечается так же синхронизация вращения Венеры относительно Земли, соизмеримость в орбитальных движениях Нептуна и Плутона (3:2), Юпитера и Сатурна (2:5), трех галилеевых спутников Юпитера (Ио, Европа, Ганимед), четырех спутников Урана и т.д.
Периоды обращения планет-гигантов Юпитера и Сатурна приблизительно равны 12 и 30 годам соответственно, и, следовательно, отношение этих периодов близко к резонансу 2:5. Два оборота Сатурна происходят за то же время, что и пять оборотов Юпитера [12, 123, 135, 137, 138, 141]. Через 60 лет взаимные положения Юпитера и Сатурна повторяются. В этом случае между периодами обращения планет имеет место соизмеримость. Благодаря соизмеримости возникает явление, подобное тому, которое в механике называется резонансом. Резонанс возникает тогда, когда на колеблющееся тело, в такт его колебаниям действует дополнительная периодическая сила [14]. Такая дополнительная сила, даже в том случае, если ее величина очень мала, постепенно приводит к появлению больших взаимных возмущений в движении этих планет и увеличению амплитуды колебаний орбитальных элементов.
Наиболее убедительное объяснение синхронизаций и соизмеримостей в движениях планет и их спутников связано с механизмом приливного трения [42, 100, 277, 278]. В основе этого механизма лежит представление о диссипации энергии гравитационных возмущений в небесных телах из-за отсутствия в них идеальной упругости. Под действием приливного трения во вращающейся планете происходит возрастание больших полуосей орбит ее спутников, которые постепенно удаляются от планеты (т.к. в результате трения происходит общее замедление вращения и обращения). За счет гравитационного взаимодействия передается момент количества движения от одного спутника к другому, их периоды обращения становятся взаимосвязанными, что приводит к появлению соизмеримости в движении. В пределе, когда угловые скорости вращения и движения по орбите практически уравниваются, переноса момента движения не происходит, происходит только обмен приливной энергией. Аналогичную природу имеет и механизм синхронизации.
Интересным примером орбитального резонанса служит резонанс в движении трех (из четырех) галилеевых спутников Юпитера. Ио находится в резонансе 2:1 с Европой, которая сама в свою очередь находится в резонансе 2:1 с Ганимедом; в результате имеется резонансная конфигурация из трех спутников известная как резонанс Лапласа. Спутники Сатурна Мимас и Тефия находятся в резонансе 4:2, Энцелад и Диона – в орбитальном резонансе 2:1, Титан и Гиперион находятся в орбитальном резонансе 4:3. Малые спутники Урана Розалинда и Корделия близки к резонансу 5:3. Пояс астероидов также имеет резонансную структуру [138, 251, 329, 345, 372, 378]. У большинства из них найдены соизмеримости с движением Юпитера (например, Троянцы), неподалеку от которого расположено основное количество этих небесных тел. При этом оказалось, что астероиды распределены группами, т.е. дискретно. В пространстве занимаемым астероидным поясом (от 2,17 до 3,64 а.е.) обнаружено несколько областей, в которых астероиды отсутствуют (как бы «запрещенные» орбиты). Они получили название люков Кирквуда; в них периоды обращения кратны периоду обращения Юпитера, и в этих областях пространства отмечаются максимальные приливные возмущения, которые являются препятствием для локализации в этой области небесных тел. Так, например, почти нет астероидов, для которых средние расстояния от Солнца были бы близки к 3,27; 2,84; 2,5 а.е. Небесные тела с такими средними расстояниями от Солнца должны обладать периодами обращения равными 5,9; 4,8; 4,0 года соответственно, что составляет 1/2; 2/5; 1/3 периода обращения Юпитера. Приливное действие Юпитера максимально на соизмеримых орбитах. Поэтому попавшие на эти орбиты тела постепенно выталкиваются с таких орбит или разрушаются в результате периодического действия приливных сил. Это приводит к появлению так называемых «полос избегания» или «люков» в распределении средних расстояний астероидов от Солнца [138].
На основе численного интегрирования было показано, что спустя небольшой промежуток времени (около 2400 лет) большая часть астероидов, находящихся в области между орбитой Юпитера и орбитой, соответствующей соизмеримости 3/2, будет оттуда выброшена; исключения составляют астероиды, совершающие устойчивые колебания (группа Гильды). Возмущающее действие Юпитера и Сатурна на первоначально однородное распределение астероидов в области между орбитами этих планет, должно привести к выбросу из этой области, по крайней мере, 85% астероидов всего за 6000 лет [138], что, вероятно, может стать причиной, известного в метеорологии «эффекта бабочки».
Среди троек средних движений (или пар относительных средних движений) в Солнечной системе есть тенденции к соизмеримости, и вероятность того, что это является случайным процессом, составляет 0,006 [124, 138, 249]. В Солнечной системе среди троек близких к точным резонансам находятся, например, Венера, Земля и Марс (n3 – n2) / (n1 – n2) = 0,74865; n1, n2, n3 – средние движения (средние угловые скорости) Венеры, Земли и Марса соответственно (табл. 1). Разности средних движений Марса и Земли, Венеры и Земли относятся почти как 3:4.
Таким образом, Солнечная система, представляет собой весьма сложную колебательную систему и имеет резонансную структуру как результат длительной эволюции [116, 117, 325–327]. Это согласуется с выводами исследований (численного интегрирования уравнений движения для 11-ти гипотетических компланарных планетных систем) Ж. Хиллса о том, что все системы в результате взаимодействий их элементов стремятся прийти в квазиустойчивое состояние. При этом в каждом случае прослеживается тенденция: периоды соседних планет оказываются почти соизмеримыми (отношение периодов близко к отношению малых целых чисел). Позднее М. Овенден подтвердил, полученный Хиллсом результат и показал, что отношение средних движений любой пары планет чаще всего оказывалось (в процессе численного интегрирования) близким к рациональной дроби с малыми целыми членами [138, 282, 337].
Вопросы, связанные с резонансами образуют проблему известную в небесной механике как проблема малых знаменателей (впервые малые знаменатели были обнаружены Лапласом при изучении движения Юпитера и Сатурна вокруг Солнца). Это проблема астрономическая и математическая [9, 39, 48, 94, 121, 133, 137, 210]. Она возникла при математических исследованиях – интегрировании дифференциальных уравнений движения планет и их спутников в поле тяготения с использованием рядов Фурье.
Как уже отмечалось, движения планет и их спутников математически могут быть представлены в виде комбинаций бесчисленного множества периодических движений с разными периодами (или частотами). При этом можно выделить основные, или главные частоты. К ним, например, относятся частоты, соответствующие средним угловым скоростям движения планет по гелиоцентрическим орбитам (связанные со средними периодами обращения планет вокруг Солнца). В астрономии эти основные частоты называются средними движениями (табл. 1.2). Если основные частоты в движении двух планет вокруг Солнца находятся в близкой соизмеримости (т.е. их отношение приблизительно равно отношению двух целых чисел), то в этом случае и возникает проблема малых знаменателей. Математический эффект малых знаменателей проявляется в том, что в решениях уравнений движения появляются периодические члены с коэффициентами, знаменатели которых близки к нулю и, следовательно, появляются периодические компоненты с большими амплитудами [38, 39, 48]. В движениях планет при этом появляются эффекты, называемые в физике резонансными (амплитуды при резонансах неограниченно возрастают).
Собственно основная проблема малых знаменателей заключается в том, что они, во-первых, препятствуют построению достаточно точных решений уравнений движения методами классической математики и астрономии (разработанных Лагранжем, Лапласом, Гауссом и др.). Во-вторых, малые знаменатели появляются во всех случаях, если при решении уравнений движения используются ряды Фурье. Все это препятствует построению точных решений уравнений небесной механики в виде сходящихся бесконечных рядов (если сумма Sn первых членов ряда стремится к пределу, когда стремится к бесконечности). В связи с этим возникает проблема, ограничивающая возможности получения строгих выводов о движении планетных систем и их эволюции на больших интервалах времени (космогонических масштабов). Основной вопрос проблемы малых знаменателей связан, таким образом, с вопросом устойчивости Солнечной системы на неограниченном промежутке времени.
Другой важный вопрос проблемы малых знаменателей связан с поисками приближенных решений уравнений движения небесных тел (связанных резонансными соотношениями) с заданной точностью. Поскольку резонансные явления встречаются не только в задачах небесной механики, но и в физике, и в той области знаний, которую принято называть нелинейной механикой, вопрос о малых знаменателях и, о методах их исследования выходит за пределы астрономической науки.
В физике и нелинейной механике эффект малых знаменателей называется явлением резонанса частот. Мерой классификации резонансов является его порядок. Применительно к системам с двумя частотами существует такая классификация резонансов (Ю. Мозера), согласно которой порядком резонанса n1 : n2 = p : q называется число p–q, где p и q – целые числа (предполагается, что n1 ≥ n2). Если p1 – q1 < p2 – q2, то резонанс с числами p1 q1 считается резонансом низшего порядка по сравнению с резонансом p2 q2. В этой системе классификации, например, система Солнце – Юпитер – Сатурн есть резонансная система 3-го порядка. Порядок резонанса в значительной степени определяет интенсивность резонанса: при возрастании порядка – интенсивность уменьшается [124].
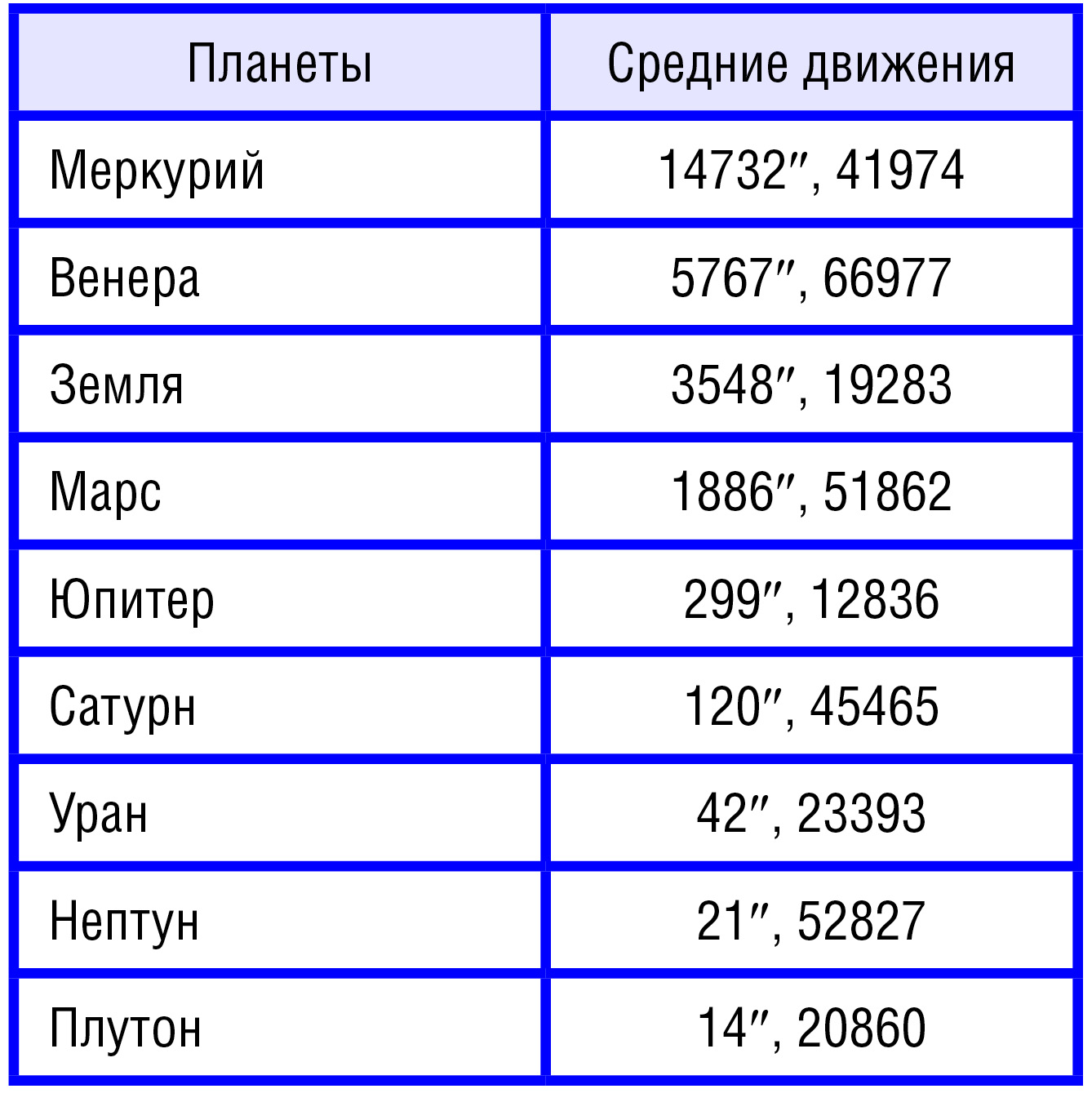
Знание средних суточных движений больших планет, спутников и других небесных тел (вычисляются делением 360° на средний период обращения) дает возможности по расчету резонансных отношений (табл. 1.2)
Таблица 1.2
Значения средних суточных движений
(на эпоху 1950, январь, 0) больших планет [39]
Предполагается, что Солнечная система в процессе эволюции проходит через несколько резонансных состояний, причем время пребывания системы в резонансных состояниях на много порядков больше времени ее пребывания в нерезонансных состояниях. В периоды резонансных состояний определяющими силами в системе являются силы взаимного тяготения. В периоды нерезонансных состояний, наряду с ньютоновской силой взаимного притяжения, активным фактором становятся приливные силы, которые в значительной мере создают и, в свою очередь, разрушают сами резонансные состояния системы [39, 42, 124, 134, 138].
Динамика Солнечной системы, с давних времен была примером правильного, детерминированного движения, которое допускает долговременное предсказание с очень высокой степенью точности. Однако, в ней, как в почти любой другой многомерной нелинейной колебательной системе, возможно движение, имеющее качественно иную природу. Это движение (получившее название динамический хаос) при котором траектория становится случайной, т.е. очень неустойчивой и непредсказуемой [52, 89–91, 94, 121]. Таким образом, предполагается, что в космосе одновременно существуют движения упорядоченные (регулярные) и беспорядочные (хаотические). Согласно гипотезе Арнольда, которая была подтверждена численными (компьютерными) экспериментами, присутствие хаотических компонентов движения для определенных начальных условий (чувствительность к начальным условиям) – это обычное явление в нелинейных колебаниях [52, 94, 137, 241]. В настоящее время известно, что любое возмущение, особенно регулярное, равномерно вращающегося третьего тела, создает конечный хаотический слой на границе невозмущенных эллиптических траекторий [52, 82, 241].
Современные исследования динамики Солнечной системы определили важную роль хаотических движений в динамической эволюции Солнечной системы [137, 373–377]. Первоначально, при использовании отображения и в процессе численного интегрирования дифференциальных уравнений Виздомом было обнаружено явление неожиданного увеличения эксцентриситета орбит астероидов (рис. 1.3). Были определены их произвольные переходы (скачки) от орбит с малым эксцентриситетом к орбитам с большим эксцентриситетом в интервале времени от 50 до 250 тысяч лет [137, 373, 376].
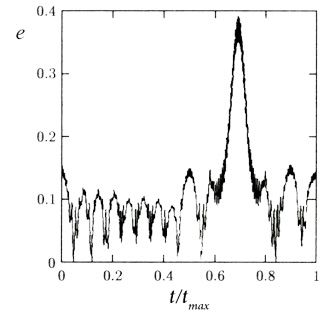
Рис. 1.3. Зависимость эксцентриситета (e) от времени,
полученная с помощью решения неусредненных дифференцированных уравнений
в плоско-эллиптической ограниченной задаче трех тел,
для хаотической траектории; tmax соответствует 16 000 периодам Юпитера
или приблизительно 190 000 лет [373]
Численное исследование устойчивости ориентации осей вращения (наклонения) планет в зависимости от вековых орбитальных возмущений показывает, что планеты земной группы в прошлом могли испытывать значительные хаотические изменения наклонений в отдельные периоды их существования. Наклонение Марса до настоящего времени находится в широкой хаотической зоне (рис. 1.4), простирающейся от 0° до 60° [137. 317].
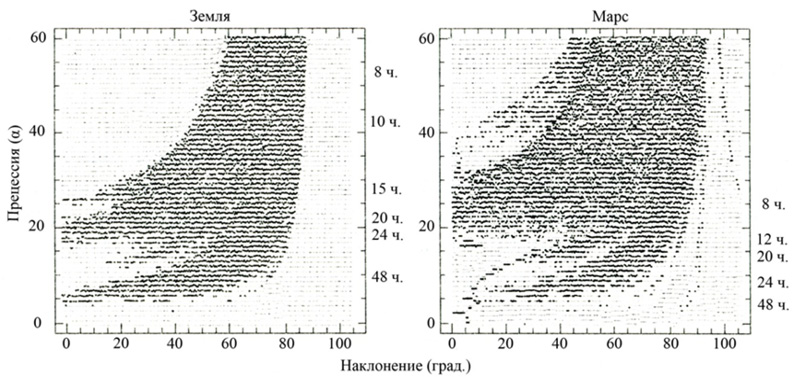
Рис. 1.4. Зоны крупномасштабного хаотического поведения величины наклонения Земли (без Луны) и Марса в широком диапазоне изменения скорости вращения планеты. Постоянная прецессии α в угловых секундах в год обозначена слева, соответствующая ей оценка периода вращения планеты (в часах) – справа. Регулярные решения представлены маленькими точками (светлый фон); решения, описывающие крупномасштабное хаотическое поведение, обозначены большими черными точками. Хаотическое движение оценивается по степени размывания частоты прецессии, полученной с помощью численного частотного анализа на интервале 36 млн. лет. В видимых здесь хаотических зонах хаотическая диффузия имеет место на горизонтальных линиях (α – фиксировано), и величина наклонения планеты может проходить всю зону, обозначенную черными точками, в горизонтальном направлении за несколько миллионов лет. При наличии Луны можно считать, что состояние Земли в настоящее время приближенно может быть представлено точкой (с наклонением равным 23° и α = 55° год–1) которая попадает в середину зоны регулярного движения. При отсутствии Луны, для периода вращения в пределах от 12 до 48 часов наклонение Земли подверглось бы очень значительным хаотическим изменениям [317]
Недавние исследования указывают на то, что и орбитальное движение Земли может быть хаотическим. При исследовании глобальной устойчивости прецессии Земли для многих значений ее скорости вращения обнаружено, что для всего первоначального периода вращения от 12 до 48 часов, наклонение Земли будет испытывать очень большие хаотические вариации приблизительно от 0° до 85°, которые возможно приведут к кардинальным климатическим изменениям. Типичные изменения приблизительно от 0° до 60° могут возникнуть меньше чем через 2 млн. лет [313–316].
В классической небесной механике разработаны многие методы исследования вращательного и орбитального движения тел Солнечной системы [48, 142]. Они относятся как к консервативным системам (например, задачи двух или трех тел), так и диссипативным системам, возникающим при учете приливной эволюции. Однако, получаемые в результате применения этих методов уравнения имеют одно общее свойство: они описывают системы, являющиеся детерминированными. Это означает, что знание текущего состояния системы позволяет вычислять ее состояния в прошлом и будущем, если известны все действующие силы. В задаче двух тел уравнение движения имеет решение, которым определяется поведение системы на любом интервале прошлого или будущего (задача интегрируема). Причина не интегрируемости связана с резонансами [43, 133]. В задаче трех тел найти полное аналитическое решение оказалось невозможным (задача не интегрируема; решение найдено для ограниченной задачи трех тел, получены частные решения для этой задачи). Поэтому для вычисления орбитального поведения небесных тел используются численные методы. При этом предполагается, что если известно начальное состояние системы, то можно вычислить ее состояние в будущем, решив уравнение движения. Однако, для некоторых систем это предположение неверно; причиной этому служит феномен, называемый хаосом (экспоненциальное разбегание близких в начальных условиях траекторий).
Исходя из предположений Лапласом теории вековых возмущений получено аналитическое решение задачи многих тел. Это решение не дает информации об угловых положениях тел на орбитах, но позволяет вычислять на любой момент прошлого или будущего другие орбитальные элементы, зная их текущие значения. Решение Лапласом вековой задачи стало обоснованием представления о долговременной устойчивости Солнечной системы [49, 141]. Лаплас исходил из представлений о детерминированности Вселенной, в которой полное знание о поведении системы, если законы природы известны, сводится к вопросу о знании начальных условий и решений соответствующих уравнений. В современной небесной механике высказываются идеи о том, что эти представления неверны [124].
В конце XIX века Пуанкаре приступил к исследованию задачи трех тел. Его основополагающие результаты показали чрезвычайно сложную природу движения, которая может проявляться в решениях этой задачи. Было очевидно, что при определенных начальных условиях траектории имеют весьма необычный характер. Так появились основы для дальнейшего исследования хаоса. Прогресс в исследовании проблемы устойчивости в движении динамических систем был намечен работами К.Л. Зигеля (1942) и А.Н. Колмогорова [69].
КАМ–теория (Колмогорова – Арнольда – Мозера) рассматривает влияние резонансов на траектории. Она показывает, что резонансы приводят к траекториям двух типов, возникающим в окрестностях резонанса: траекториям регулярным и траекториям со случайным поведением [52, 94, 115, 133]. «Типичным случаем в многомерных задачах теории возмущений является комбинация топологической неустойчивости с метрической устойчивостью условно-периодических движений» [9]. Основной результат КАМ–теории состоит в том, что определены два, совершенно различных, типа траекторий: слегка изменившиеся (деформированные) квазипериодические траектории (при малом возмущении) и стохастические траектории, возникшие при разрушении резонансных торов [9, 43, 52]. Из полученных КАМ–теорией результатов, в частности вытекает «топологическая неустойчивость планетных движений». Как отмечает Арнольд: «результаты не исключают возможности того, что сколь угодно малое изменение начальных условий способно совершенно изменить характер движения за бесконечное время» [9]. Наиболее важный результат КАМ–теории – появление стохастических траекторий – подтверждается численными экспериментами [121, 133, 137]. Однако эта теория имеет, ограничивающие ее, условия: наличие только малых возмущений и отсутствие соизмеримости низких порядков. Эти условия не выполняются в Солнечной системе [38, 141].
Благодаря появлению компьютеров и росту их производительности в исследованиях нелинейной динамики Солнечной системы возник новый – численно – экспериментальный подход. К настоящему времени численные результаты, вместе с новыми данными наблюдений и теоретическими разработками, выявили важнейшую роль хаоса в формировании динамической структуры Солнечной системы и ее эволюции [137, 138]. Ласкаром разработан метод исследования хаотического движения Солнечной системы, основанный на анализе вариаций фундаментальных частот с течением времени (численный анализ фундаментальных частот – вращения и обращения). Этот метод позволяет определить, является ли решение хаотическим за меньший промежуток времени, чем метод показателей Ляпунова (классический метод обнаружения хаотического движения заключается в вычислении характеристических показателей Ляпунова), а также позволяет получить оценку размера зон хаоса [88, 89, 90, 313]. Метод позволяет обнаружить хаотическую орбиту на коротком временном интервале, в противоположность критерию показателя Ляпунова [89, 97]. Напомним, что время Ляпунова – это время, за которое система приводится к полному хаосу. Оно определяется как время, за которое расстояние между соседними траекториями экспоненциально возрастает в е раз; время Ляпунова отражает пределы предсказуемости системы (для Солнечной системы оно составляет 5 млн. лет).
Общепринятого определения хаоса до настоящего времени нет, хотя он проявляется в самых разных динамических системах. Например, в классической динамике предлагается следующее определение: тело Солнечной системы движется хаотически, если его финальное динамическое состояние существенным образом зависит от его начального динамического состояния [124, 133]. Однако, поскольку результат измерения любой физической величины всегда содержит неизбежную ошибку, недостаток точности в начальных условиях всегда преобразуется в неопределенность финального состояния.
Если бы пробная частица (тело) испытывало только притяжение Солнца, то ее движение было бы совершенно предсказуемо. Однако из-за возмущений со стороны планет определенные области фазового пространства становятся хаотическими: орбитальная эволюция пробных частиц (совокупность которых образует небесное тело) в этих областях происходит непредсказуемым образом. Малая вариация начальных условий изменяет геометрию движения пробной точки и, следовательно, величину непосредственного возмущения, испытываемого со стороны планеты (рис. 1.5). Хаос, связанный с чувствительностью к начальным условиям, приводит к «невычислимым» траекториям или экспоненциальным разбеганиям траекторий [133]. В общем случае, это более чем просто техническая сложность в измерении начальных условий. Барьер связан с непрекращающимся взаимодействием (возмущением, в том числе резонансным) постоянно меняющим реальные начальные условия. В окрестностях же резонанса, согласно КАМ–теории, наряду с регулярными движениями, в результате топологической неустойчивости возникают и движения хаотические.
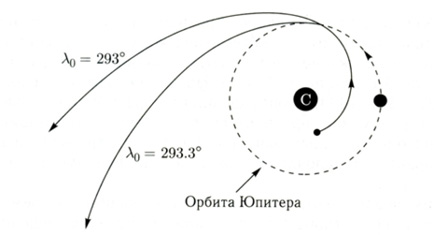
Рис. 1.5. Траектории двух пробных частиц с одинаковыми начальными значениями большой полуоси (a0 = 0,8), эксцентриситета (e0 = 0,4) и долготы перицентра (ῶ0 = 295°), но с малыми отличиями в начальных значениях средней долготы (λ0 = 293° и λ0 = 293,3°). Орбита Юпитера изображена в виде штриховой окружности; начальная долгота Юпитера принята равной нулю. Численное интегрирование проведено на интервале времени в один орбитальный период Юпитера [124]
Одним из примеров возможного хаотического движения в Солнечной системе может быть результат исследования эволюции орбиты астероида Хирона [335]. Перигелий орбиты Хирона расположен внутри орбиты Сатурна, а афелий, вблизи орбиты Урана. Используя наилучшие доступные определения элементов орбиты Хирона Оикава и Эверхарт выполнили несколько численных экспериментов по интегрированию его орбиты, при этом начальные условия принимались близкими к общепринятым для этого объекта. Эксперименты показали, что Хирон испытает в будущем несколько тесных сближений с планетами. Разные начальные условия привели к существенным различиям в конечных результатах, что является признаком хаотического поведения. Поэтому Оикаве и Эверхарту удалось дать лишь вероятностную оценку финального состояния Хирона. Вероятность того, что Сатурн перебросит Хирон на гиперболическую орбиту, уводящую Хирон из Солнечной системы, они оценили как 1 из 8. Вероятность того, что сближения Хирона с Сатурном заставят его орбиту эволюционировать в направлении внутренней части Солнечной системы (где он попал бы под действие гравитационных возмущений Юпитера), больше: 7 из 8.
Отмечаются и более сложные формы проявления хаоса. Так, результаты двух численных экспериментов по интегрированию уравнений движения в круговой ограниченной задаче трех тел показывают, сходную эволюцию двух орбит в течение интервала времени, равного примерно 150 орбитальным периодам Юпитера (около 1800 лет), после которого орбиты начинают постепенно расходиться. Очевидной причины для этой бифуркации нет (например, на интервале времени интегрирования отсутствуют сближения с Юпитером), но, тем не менее, в этом примере проявляется характерное свойство хаоса: орбиты существенно зависят от начальных условий (рис. 5).
Таким образом, наряду с регулярными движениями в Солнечной системе существуют движения хаотические [124]. Хаотическое движение в ряде работ рассматривается как результат резонанса, так и результат перекрытия смежных резонансов [94, 124]. Принято считать, что каждый резонанс сопровождается, различной по величине, хаотической зоной [89, 90, 137, 241, 251, 279, 377]. Из-за значительных изменений элементов орбит при хаотическом движении, хаотические орбиты могут проникать (диффузия) в области фазового пространства, недоступные для регулярных орбит [124, 377]. Установлено, что наклон оси вращения каждой из планет земного типа мог в прошлом хаотически колебаться (а, значит и палеоклимат). В случае Марса амплитуда таких колебаний могла доходить до нескольких десятков градусов [137, 317, 354]. Хаотическим изменениям, вероятно, были подвержены и эксцентриситеты планетарных орбит. Это подтверждается результатами расчетов орбиты пробной частицы выполненных Виздомом [373, 376], которые показывают, что при некоторых начальных условиях орбита пробной частицы вблизи резонанса 3:1 может вести себя как регулярная в течение десятков и сотен тысяч лет, а затем испытывать сильный скачок эксцентриситета. При этом эксцентриситеты орбит объектов вблизи резонанса 3:1 с Юпитером под влиянием возмущений со стороны других планет могут достигать значений более 0,6; т.е. такие объекты могут пересекать орбиту Земли [375]. Из исследования планетарных орбит внешних планет так же следует, что хаотическая орбита может выглядеть как регулярная на больших интервалах времени, прежде чем ее хаотическая природа становится очевидной [351]. При исследовании динамики всех планет Солнечной системы на интервале времени в 10 млн лет Ласкаром [314] было проведено численное интегрирование усредненных уравнений движения (усредняются короткопериодические эффекты). В результате было показано, что внутренние планеты движутся хаотически. При этом время экспоненциальной расходимости траекторий составляет 5 млн. лет (максимальный показатель Ляпунова 10–6,7 год–1). Сходное значение (4 млн. лет) было найдено Сусманом и Виздомом [350], которые выполнили интегрирование в полной задаче для всех планет Солнечной системы на интервале времени в 100 млн лет. Они показали также, что орбиты четырех планет – гигантов являются хаотическими. Напомним, что характеристические показатели Ляпунова – отражают среднюю скорость экспоненциального расхождения (>0) или схождения (<0) изначально близких фазовых траекторий; т.е. при положительном значении показателя – система хаотична [47, 97].
Все известные результаты численных экспериментов по интегрированию согласуются в том, что планеты движутся по хаотическим орбитам. Однако, ни в одном из них не было найдено указаний на крупномасштабную неустойчивость (даже при интегрировании на временных интервалах, сопоставимых с возрастом Солнечной системы). Планеты движутся по хаотическим орбитам, но этот хаос незаметен. Его существование означает, что возможности предсказывать положения планет на больших интервалах времени ограничены фундаментальным пределом. Если бы начальные положения и скорости планет были известны абсолютно точно, то при использовании идеального интегратора, можно было бы абсолютно точно вычислять положения планет на орбитах в будущем или прошлом. Однако, поскольку любое физическое измерение имеет конечную точность, при вычислениях всегда есть изначально «встроенная» ошибка. В хаотической системе эта погрешность будет расти по экспоненте. В случае планет, например Земли, это означает, что предсказать положение Земли на орбите в отдаленном будущем невозможно. Например, величина максимального показателя Ляпунова 10–6,7 год–1 означает, что погрешность определения координат Земли, равная в настоящее время, допустим, 1 см будет возрастать так, что оказывается невозможным предсказать положение Земли в будущем, отстоящим от нас более чем на 200 млн лет [124].
При исследованиях солярного климата Земли следует учитывать понятие о том, что наличие резонансов и хаотического движения препятствует решению уравнений движения на значительных по продолжительности временных интервалах, в связи с возможными получениями хаотических (а не периодических и условно-периодических) решений. Как результат экспоненциального расхождения орбит (диффузии) возникает предел (по времени) для возможности создания точных предположений о движении небесных тел (изменении их эксцентриситета, наклонения и других элементов орбиты) – фундаментальное ограничение по времени [47, 88, 89, 124]. Следовательно, точные расчеты приходящей солнечной радиации к Земле для длительных интервалов времени (как в будущее, так и в прошлое) невозможны.
1.2. Законы теплового излучения
Свечение тел при их нагревании называется температурным или тепловым излучением. В этом случае энергия внутренних хаотических тепловых движений частиц тела (при Т > 0 К) непрерывно переходит в энергию испускаемого электромагнитного излучения. Основной количественной характеристикой теплового излучения тела является его лучеиспускательная способность (eT), т.е. лучистая энергия, испускаемая единицей поверхности тела за единицу времени (эрг/см2 × сек или Дж/м2 × сек = Вт/м2) при температуре тела T. Эта энергия переносится электромагнитными волнами различной длины (0 ≤ λ ≤ ∞) и при изучении излучения полная лучеиспускательная способность тела (eT) анализируется в различных диапазонах длин волн. Энергия электромагнитных волн с длиной от λ до λ + dλ, испускаемая единицей поверхности излучающего тела за единицу времени, пропорциональна величине выделенного интервала длин волн:
Коэффициент пропорциональности eλ,T есть лучеиспускательная способность тела при данной температуре T для данной длины волны λ, и имеет размерность Вт/м3 (т.е. рассчитывается на единицу интервала длин волн dλ = 1). Полная лучеиспускательная способность тела eT складывается из элементарных интервалов deT, т.е.
где интеграл распространен на весь бесконечный интервал всевозможных длин волн [56, 57, 85, 86, 145].
С ростом температуры увеличивается интенсивность теплового движения частиц и, возрастает энергия, излучаемая телом с электромагнитными волнами любых λ. При абсолютном нуле температуры (Т = 0 К) тепловое излучение отсутствует и eλ,0 ≡ 0, т.е. тело не может далее уменьшать своей энергии и его тепловое излучение прекращается.
При тепловом излучении энергия теплового движения в теле переходит в энергию испускаемых электромагнитных волн. При поглощении света происходит обратный процесс перехода лучистой энергии в тепловую энергию тела. В обоих случаях взаимные превращения тепловой и лучистой энергии протекают через промежуточную стадию колебания электрических зарядов в теле. Поэтому лучеиспускательная и лучепоглощательная способности тела обусловлены одними и теми же деталями его строения и тесно связаны между собой. При этом отношение полной лучеиспускательной способности любого тела к его же поглощательной способности при данной температуре есть величина постоянная, равная испускательной способности абсолютно черного тела при той же самой температуре. Это соотношение было найдено в 1860 году Г. Кирхгофом (Kirchhof). Закон, названный его именем, формулируется следующим образом. Отношение лучеиспускательной и поглощательной способности для любых тел при одинаковой их температуре Т и для одной и той же длины волны λ одинаково и не зависит от природы этих тел. Это отношение является универсальной функцией длины волны и температуры и равно лучеиспускательной способности абсолютно черного тела Eλ,T:
Поскольку для абсолютно черного тела лучепоглощение a = 1 (поглощает все падающие на него лучи), а для других тел aλ,T < 1, то из закона Кирхгофа следует весьма важное утверждение. Излучение, которое тело сильнее поглощает, сильнее и испускается. При данной температуре
,
т.е. тепловое излучение абсолютно черного тела во всех частях спектра интенсивнее, чем для нечерного тела, нагретого до той же самой температуры.
В 1878 году Й. Стефаном (Stefan), а в 1884 году Л. Больцманом (Boltzmann) была доказана пропорциональность полной лучеиспускательной способности абсолютно черного тела четвертой степени его абсолютной температуры т.е.
Это соотношение получило название закона Стефана – Больцмана.
Исследуя спектральное распределение излучения В. Вин (Wien) показал, что максимум лучеиспускательной способности находится на некоторой длине волны λmax, которая связано с абсолютной температурой T соотношением
Таким образом, с ростом температуры максимум лучеиспускательной способности абсолютно черного тела смещается в сторону более коротких волн. Это соотношение получило название закона смещения Вина [56, 57, 79, 85, 145].
Это законы волновой электромагнитной теории света. Однако, физики столкнулись с проблемами при изучении излучения с короткими длинами волн («ультрафиолетовая катастрофа»), что указало на теоретические дефекты и необходимость пересмотра принципиальных положений этой теории. В 1901 году М. Планк высказал предположение о том, что излучение испускается телами не непрерывно, но в виде отдельных порций (дискретно). Энергия каждой такой порции – кванта излучения – пропорциональна его частоте:
где h – универсальная постоянная, одинаковая по всему спектру и получившая впоследствии название постоянной Планка (6,62 × 10–34 Дж × сек). В результате Планк получил выражение для лучеиспускательной способности абсолютно черного тела (формула Планка):
Согласно формуле Планка для каждой данной длины волны λ с ростом температуры показатель и величина, стоящая в знаменателе, , убывают, а сама дробь возрастает. Следовательно, с ростом температуры возрастает и лучеиспускательная способность во всех участках спектра, но в различной степени. Из формулы Планка вытекают также законы теплового излучения Стефана – Больцмана и Вина [11, 56, 57, 71, 74, 79, 86, 145, 202].
1.2.2. Распространение излучения
Для пространственных задач распространения излучения существенно понятие о телесном угле [57, 85, 129]. Мерой телесного угла является отношение площади dS0 участка, вырезаемого конусом на поверхности сферы к квадрату ее радиуса r, т.е. dω = dS0/r2 (рис. 1.6). За единицу телесного угла принят телесный угол, опирающийся на участок поверхности сферы, площадь которого равна квадрату ее радиуса (dS0 = r2). Эта единица называется стерадиан (стер). Наибольший телесный угол равен, очевидно, 4π стер (площадь всей поверхности сферы 4πr2).
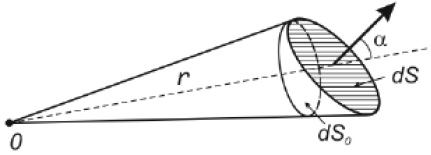
Рис. 1.6. Телесный угол
Как видно из рисунка 1.6 площадка dS, нормаль к которой n составляет угол α с радиусом r, проведенным из точки наблюдения O, видна из этой точки O, под телесным углом
Основной энергетической величиной излучения является лучистый поток Ф [57, 71, 86, 114]. Эта величина характеризует энергию, проходящую через данную поверхность за единицу времени, и измеряется соответственно в единицах мощности (Вт, эрг/сек).
На рис. 1.7 изображен точечный источник S и, выделен телесный угол dω с вершиной в точке S.
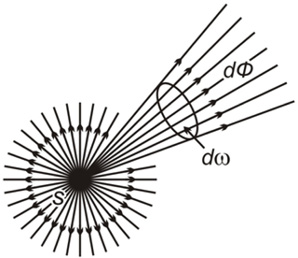
Рис. 1.7. Лучистый поток
Если обозначить лучистый поток, заключенный в телесном угле , через , тогда соотношение является силой излучения точечного источника в данном направлении. Из этого соотношения следует, что сила излучения характеризуется величиной потока, заключенного в единице телесного угла, и измеряется соответственно в Вт/стер или эрг/сек × стер. Если поток, испускаемый точечным источником, равномерный во всех направлениях, то
где Ф – полный лучистый поток, испускаемый источником по всем направлениям, т.е. во всем телесном угле ω = 4π. Если же поток неравномерен, то приведенная формула определяет среднюю силу излучения источника.
Интенсивность излучения протяженного источника характеризуется его лучистостью. Она численно равна силе излучения в данном направлении, создаваемой единицей площади видимой поверхности источника (измеряется в Вт/м2 × стер или эрг/сек × см2 × стер). Лучистость протяженного источника может быть различной в разных направлениях. Однако, для таких источников, как Солнце величина лучистости не зависит от направления наблюдения. Т.е. сила излучения (света) такого источника пропорциональна косинусу угла с нормалью (закон Ламберта) и максимальна в направлении нормали. Если поверхность испускает лучистый поток Ф по всем направлениям (в телесном угле 2π), то лучистый поток, испускаемый единицей площади, Ф/S = R характеризует плотность излучения (светимость) источника и измеряется в Вт/м2 или эрг/см2 × сек.
Понятие облученности (освещенности) E относится уже не к источникам излучения (света), а характеризует интенсивность лучистой энергии, падающей на освещаемую поверхность. Величина E численно равна величине потока, падающего на единицу освещаемой поверхности, т.е. (измеряется в Вт/м2 или эрг/сек × см2).
Если произвольно ориентированная в пространстве площадка dS освещается точечным источником O (рис. 1.6), то согласно формуле , где r – расстояние от источника до площадки, α – угол между направлением лучей и нормалью к площадке, а dω – телесный угол, под которым видна площадка dS из точечного источника O. Освещенность этой поверхности
так как есть сила света источника I. Приведенная формула выражает два закона освещенности
- Освещенность площадки обратно пропорциональна квадрату расстояния от точечного источника (закон обратных квадратов).
- Освещенность площадки прямо пропорциональна косинусу угла между направлением лучистого потока и нормалью к площадке (закон косинуса).

