8.1. Расчеты константы равновесия реакции при нестандартной температуре раствора
8.2. Расчеты константы равновесия реакции при повышенном давлении
Расчеты гетерогенного равновесия в разбавленных растворах при повышенной температуре и давлении в системе для гидротермальных процессов требует умения рассчитывать зависимость константы равновесия от температуры и давления. В принципе эту зависимость мы можем получить, используя уравнение Вант-Гоффа: RTlnK = –∆G(P, T). Используя выражение для полного дифференциала изобарного потенциала реакции, можно получить зависимости изобарного потенциала (а значит, и константы равновесия реакции) от температуры и давления:
d[∆G(P,T)]= –∆SdT + ∆VdP (8.1)
∆G(T)р = –∫∆SdT + const, ∆G(P)T = –∫∆VdT + const
Так как расчет гетерогенного равновесия в системе для гидротермальных процессов мы выполним для разбавленных растворов, нам не потребуется вычислять поправки к изобарному потенциалу реакции на неидеальность раствора.
8.1. Расчеты константы равновесия реакции при нестандартной температуре раствора
Получить зависимость изобарного потенциала реакции (и константы равновесия реакции) от температуры, можно с помощью уравнения (8.1), а можно воспользоваться определение изобарного потенциала через энтальпию и энтропию реакции. Действительно: ∆Gо(T) = ∆Hот – T∆Sот. Воспользуемся формулами Кирхгофа для расчета зависимости энтальпии и энтропии реакции от температуры, [∆H] = (Дж/моль), [∆S] = (Дж/мольК)
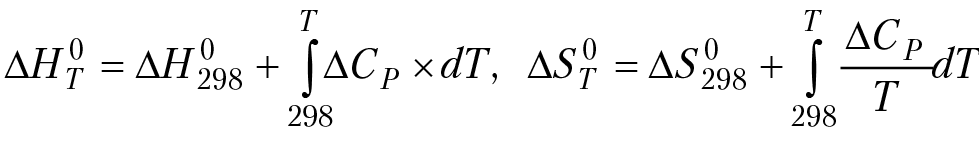
В формулах ∆Cp — изменение теплоемкости раствора в результате протекания в нем реакции, верхний индекс «0» в записи изобарного потенциала, энтальпии и энтропии реакции означает, что реакция протекает при стандартном давлении в системе. Если парциальные мольные теплоемкости компонентов реакции зависят от температуры в форме степенного ряда, Cp = a + b × T — c/T2, тогда ∆Cp = ∆a + ∆b × T — ∆c/T2 и, после интегрирования и подстановки в уравнение ∆G°т = ∆H°т — T∆S°т, получим:
∆G°т = ∆G°298 –∆S°298(T – 298,15) – ∆a × T × ln(T/298,15) + ∆a(T – 298,15) –
– 1/2 ∆b(T – 298,15)2 + 0,5 × ∆c(1/T)(T/298,15 – 1)2
∆G°298 = ∆H°298 – 298,15 × ∆S0298
Если воспользоваться обозначениями: Θ = [1 – Y], Y = 298,15/T, B = 1/(2,3026 × R) = 0,0522, pK = – lgK. pK°т = ∆G°т/(2,3026RT), получим:
∆G°т = ∆G°298 – TΘ∆S°298 + T(lnY + Θ)∆a – 0,5 × ∆b(T × Θ)2 + 0,5 × × T × ∆c(Θ/298,15)2
Зависимость константы равновесия от температуры при стандартном давлении можно записать в виде уравнения (2):
pK°T = (B/T) × ∆G°T (8.2)
Мы установили, что зависимость изобарного потенциала реакции (а значит и константы равновесия реакции) от температуры определяется зависимостью изменения теплоемкости системы ∆Cp от температуры: ∆G°т = f(∆C). Вычислим значение константы равновесия реакции для ∆Cp = ∆a + ∆b × T –∆c/T2:
pK°т = YpK°298 – BΘ∆S°298 + B∆a[lnY + Θ] – 0,5 × B∆b × T × Θ2 + 0,5 (Θ/T)2 × ∆c
Y = 298,15/T, Θ = 1 – Y, B = 0,0522 (8.3)
При расчетах константы равновесия используются различные приближения:
1) в результате протекания реакции теплоемкость системы не изменяется, ∆Cp = 0.
2) когда теплоемкость компонентов реакции не зависит от температуры, ∆Cp = const, ∆b = ∆c = 0.
3) когда ∆Cp = ∆a + ∆b × T. Именно это приближение можно считать наиболее корректным, так как для компонентов раствора теплоемкость зависит от температуры по линейному закону. Используя соотношение (8.3), получим:
1. ∆Cp = 0. pK°т = Y × pK°298 – B Θ ∆S°298.
2. ∆Cp = ∆a; pK°т = Y × pK°298 – B × Θ × ∆S°298 + B × ∆a × [lnY + Θ].
3. ∆Cp = ∆a + ∆bT; pK°т = Y × pK°298 – B × Θ × ∆S°298 + B × ∆a[lnY + Θ] – 0,5∆b × B × T × Θ2. Θ = [1 – Y].
Задача 8.1. Оценить растворимость флюорита CaF2 при температуре 50 °C и давлении насыщенного пара воды.
Решение: сначала рассчитаем ∆G°323 реакции CaF2 = Ca2+ 2F–. Выпишем из справочника необходимые для расчета термодинамические данные и воспользуемся формулой (8.1) для расчета изобарного потенциала реакции диссоциации при температуре 323 °К.
∆G°298 = –552 800 + 2(–281 700) – (–1176 920) = 60 720 (Дж/моль)
∆S°298 = –55,18 + 2(–14) — 68,87 = –152,05 (Дж/мольоК)
∆a = –59,77, ∆b = [2,9 + 2(–352) – 30,43 ]10–3 = –0,732
∆c = –1,96 × 105
∆G°323 = 60 720 + 152,05 × (323 – 298) + 59,7 × 323 × ln(323/298) – 59,77 × (323–298) +
+ 0,5 × 0,732 × (323 – 298)2 – 0,5 × 196 000 × (1/323) × (323/298 – 1)2 =
= 60720 + 4088,86 = 64 808,86 (Дж/моль)
Константу равновесия реакции диссоциации флюорита при Т = 323,15 °К и давлении 1 бар, вычислим по уравнению (8.3):
pK°323 = 10,47, K°323 = 3,39 × 10–11
Растворимость флюорита L(мг/литр) = 15,91 (мг/кг).
В таблице 8.1 собраны результаты расчета растворимости флюорита в приповерхностных гидротермальных водах при давлении 1 бар.
Таблица 8.1. Зависимость растворимости флюорита
от температуры при давлении один бар
|
T °K |
∆G°T (Дж/м) |
pK°T |
L°T (мг/л) |
|
298,15 |
60 720 |
10,63 |
14,04 |
|
323,15 |
64 809 |
10,47 |
15,91 |
|
348,15 |
69 487 |
10,42 |
16,54 |
|
373,15 |
74 688 |
10,48 |
15,80 |
8.2. Расчеты константы равновесия реакции при повышенном давлении
В предыдущем разделе главы мы установили, что зависимость свойств раствора от температуры определяется изменением теплоемкости раствора в результате протекания в нем реакций. Зависимость свойств раствора (а в общем случае термодинамической системы) от давления определяется изменением объема раствора или системы. Определим понятие парциального мольного объема компонента раствора как изменение объема системы при бесконечно малой добавке компонента в раствор. Согласно такому определению, парциальный мольный объем vo компонента раствора может быть и отрицательным. Зависимость парциального мольного объема компонента раствора от температуры и давления определяется коэффициентами объемного расширения α и коэффициентом изотермической сжимаемости β:
α = 1/vo(dvo/dT)р и α = – 1/vo(dvo/dP)т (8.4)
Для изобарных процессов в системе, зависимость парциального мольного объема компонента раствора от температуры определяется соотношением:
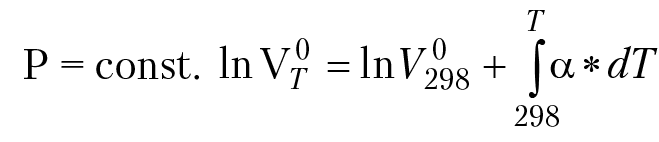
При постоянной температуре в системе зависимость парциального мольного объема компонента раствора от давления определяется соотношением:
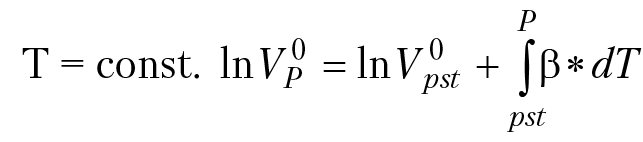
Пусть ∆V — алгебраическая разница между парциальными мольными объемами продуктов реакции и исходными веществами. Тогда:
∆b = –1/∆V(d[∆V]/dP)т , ∆β × ∆V = –(d[∆V]/dP)т (8.5)
где ∆F = ∆β × ∆V — изотермическая сжимаемость раствора.
Зависимость изменения мольного объема раствора от давления получим из уравнения:
d(∆V)p = –∆F dP
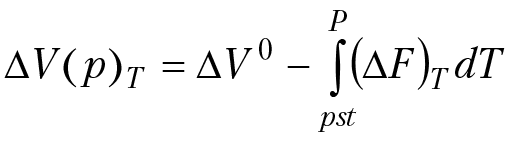(8.6)
Зависимость изобарного потенциала реакции от давления получим из анализа выражения для полного дифференциала потенциала:
d(∆G) = –∆SdT + ∆VdP, (d[∆G]/dP)т = ∆Vт (8.7)
Если проинтегрировать уравнение (36) с учетом (35), получим:
∆G = ∆G°298 + ∆VT(P – Pst) – ∫∫∆F × dP2 (8.8)
Анализ уравнения (42) показывает, что зависимость изобарного потенциала реакции от давления (в общем случае, и раствора) определяется изотермической сжимаемостью раствора, ∆F. На основании экспериментальных данных было показано, что для большого количества растворов солей и оснований в воде изменение мольного объема раствора и изотермическая сжимаемость связаны между собой линейной зависимостью:
.png)
(8.9)
При постоянной температуре зависимость константы равновесия реакции от давления определяется уравнением:
RTlnK = – ∆G(P,T)
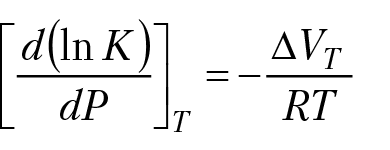(8.10)
∆Vт — изменение мольного объема раствора при температуре Т °К.
Используя уравнения (8.6) и (8.7), для зависимости константы равновесия реакции от давления при температуре раствора Т °К, получим:
lg[K(р)т] = lg(K0т) — ∆Vт(P–Pst)/(2.3026 × RT) +
+ 1/(2,3026RT)∫∫∆F × dP2 (8.12)
Kт0 — константа равновесия реакции при стандартном значении давления в системе и температуре Т °К. В уравнении (8.12) для расчета изменения мольного объема мы используем размерность ∆V [см3/моль], для расчета ∆P — бары, тогда для газовой постоянной “R” необходимо взять значение: R = 83,143 [см3бар/(моль°К)].
Пусть А = 1/(2,3026R) = 5,223 × 10–3 [мольК/(см3бар)].
∆P(бар) = P – Pst, тогда уравнение (8.12) преобразуется к виду:
lg[K(P)т] = lgK°т — (А/Т)[ ∆V°т × ∆P – ∫∫∆F×dP2]
В уравнении: К(P)т — константа равновесия реакции при температуре раствора Т °К и давлении в системе Р(бар), К°т — константа равновесия реакции при давлении в системе 1 бар, ∆V°т(см3/моль) — изменение мольного объема раствора в результате протекания реакции при давлении Р = 1 бар и температуре Т °К. При расчетах зависимости константы равновесия от давления пользуются различными приближениями, связанные, в основном, с расчетом изотермической сжимаемости системы ∆F при реакции.
1. ∆F = 0. Тогда ∆V = const и для константы равновесия получим:
lnK(P)т = lgKот – (А/Т)∆Vт(P – Pst), А = 5,223×10–3 (8.13)
2. ∆F = const. При стандартной температуре и давлении [∆V°/∆F°]298 = 4700 бар и ∆Fт/∆F°298 = ∆Vт/∆V°298. α = 1,064 × 10–4, ∆P[бар] = P – Pst. Получим:
lg[K(P)]т = lgKот – A/T × ∆V°т × ∆P(1 – α × ∆P)
3. ∆F = ∆β × ∆V. Считая, что ∆β не зависит от давления, из уравнения (8.12) и экспериментальных данных получим:
∆β ≈ 1,5 × 10–4 [бар]–1 до t ≈ 200 °C и
∆β ≈ 3,0 × 10–4 [бар]–1 для t ≈ 200 × 350 °С
lg[K(P)т] = lgKот – A/T × ∆V°т × [1 – 0,5∆β × ∆P] × ∆P, (8.14)
∆P = P – Psт, А = 5,223 × 10–3
Задача 8.2. Оценить растворимость флюорита при температуре 50 °С и давлении 500 бар.
Решение: воспользуемся результатами расчетов, проделанных в задаче (8.1) Растворимость флюорита CaF2 вычислим по формуле: pL = pK/3 – 4,691. Для расчета константы равновесия воспользуемся уравнением (8.14):
lgKp = lgK°323 – 0,1 × ∆V°323 × ∆P[1 – γ × ∆P]/2,3026 × R × 323,15 × × ∆Vо323 = –30,4–2 × 4,8–24,542 = –43,34 (см3/моль);
∆P = 500 – 1 = 499 бар.
γ = 0,5 × [∆F°298/∆V°298 ] = 0,5/4700 = 1,06 × 10–4;
K°323 = 3,31 × 10–11, pK[323 °K, 500 бар] = 10,47 – 0,33 = 10,14,
pL = –1,3113, L = 20,48 (мг/литр).
Расчетная растворимость флюорита при различных параметрах раствора:
L [25 °С, Р = 1 бар] = 14,05 (мг/кг);
L [50 °С, Р = 1 бар] = 15,89 (мг/кг);
L [50 °С, Р = 500 бар] = 20,48 (мг/кг).