Физическая химия

7.1. Учет электростатического взаимодействия ионов в растворе

7.2. Методы расчета коэффициента активности электролита

7.3. Термодинамическая и концентрационная константы равновесия реакции

7.4. Методы прямого учета электростатического взаимодействия ионов при расчете изобарного потенциала

7.1. Учет электростатического взаимодействия ионов в растворе

В теории разбавленных растворов предполагается, что частицы растворенного вещества взаимодействуют только с молекулами растворителя. При повышении концентрации раствора необходимо принимать во внимание взаимодействие частиц в растворе между собой. Это может быть сделано разными способами. Мы воспользуемся результатами работы Льюиса. Для описания термодинамиче­ских свойств реальных растворов Льюис ввел понятие термодинамическая активность компонента раствора или просто активность. По определению, активность компонента раствора а = γm; m [моль/кг] — моляльная концентрация компонента, γ — коэффициент активности. С помощью понятия активность компонента раствора можно применять к реальному раствору термодинамические соотношения, относящиеся к разбавленному раствору, если заменить в них концентрации активностями. Отклонение коэффициента активности γ от единицы указывает на степень отклонения свойств раствора от поведения разбавленного раствора. В данной модели реального раствора взаимодействие частиц друг с другом учитывается умножением концентрации компонента на коэффициент активности компонента. Естественно, изменяется и термодинамические характеристики компонента реального раствора: выражение для химического потенциала компонента реального раствора будет иметь вид: µ = µ° + RTln[a]. Так как а = γm, µ = µ° + RTln(γ[m]) = RTln[m] + RTln(γ). Слагаемое RTln(γ) учитывает взаимодействие компонентов раствора с данным компонентом. Очевидно, что для того, чтобы построить термодинамику реальных растворов, надо уметь вычислять коэффициенты активности. В теории электролитов предложены различные способы вычисления коэффициента активности, а значит и химического потенциала компонента раствора (формулы Дебая—Хюккеля, Питцера и т. д.). В случае неэлектролитов, коэффициенты активности определяются экспериментально.

Растворы электролитов. Растворы, хорошо проводящие электрический ток, называют электролитами. Вещества, при растворении которых получаются электролиты, так же называют электролитами. Электролиты получаются при растворении в воде веществ с ионной кристаллической решеткой (например, солей NaСl, KСl) или веществ с полярной ковалентной связью, например HСl(газ), HBr(газ). Растворение этих веществ сопровождается диссоциацией с образованием ионов в растворе. В растворе ионы связываются с молекулами воды с образованием гидратной оболочки. Образование электролитов за счет диссоциации вещества в воде лежит в основе теории электролитической диссоциации шведского ученого С. Аррениуса (1900). Аррениус ввел понятие степени диссоциации: отношение числа молекул электролита, распавшихся на ионы к общему числу его молекул в растворе. Если обозначить концентрацию электролита через m (моль/кг), степень его диссоциации в растворе через α, то концентрация каждого из ионов будет равна mα, концентрация недиссоциированных молекул будет равна m(1–a). Уравнение для константы диссоциации реакции АВ = А+ + В– будет иметь вид:

Отметим, что константу диссоциации электролита мы можем вычислить по уравнению Вант-Гоффа: RTlnK = –∆G°298, а значит, и степень диссоциации электролита.

7.2. Методы расчета коэффициента активности электролита

Одним из основных понятий термодинамики является химический потенциал компонента раствора. В теории разбавленных растворов для вычисления химического потенциала мы имеем уравнение: µi = µ0i + RTln[mi]. С учетом межмолекулярного взаимодействия компонентов раствора, согласно представлениям Льюиса, мы должны записать для химического потенциала выражение: µi = µ0i + RTln(miγi), где miγi = ai активность компонента раствора. Для электролитов, Дебай и Хюккель предложили формулу для расчетов коэффициентов активности γi:

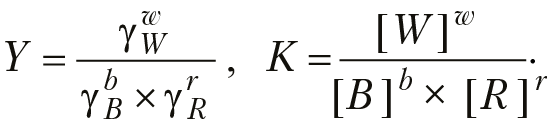
где A и B — параметры, зависящие от свойств растворителя и температуры. Для стандартных условий и воды, A = 0,5091[кг1/2моль–1/2], B = 0,3283 × 108 [кг1/2моль–1/2см–1]. I = 0,5ΣmiZ2i — ионная сила раствора. ri в теории Дебая — Хюккеля определено как «среднее расстояние сближения ионов». Точное физическое определение этой величины затруднено, поэтому параметр ri рассматривается как некоторая эмпирическая константа, которая зависит от размеров иона. Величина параметра ri близка к размерам ионов в кристаллических решетках, таблица 7.1. Среднее значение ri = 0,45 × 10–8 см может быть использовано для растворов с ионной силой I < 0,05. Приведенное уравнение Дебая—Хюккеля считается пригодным для расчетов коэффициентов активности ионов в растворах с ионной силой I < 0,25. Дальнейшее усовершенствование теории (для приложения ее к более концентрированным растворам) пошло по пути учета поляризуемости молекул воды ионами растворенного вещества. Это потребовало введения полуэмпирических параметров, что идет в ущерб цельности теории. Для увеличения интервала концентраций, охватываемого электростатической теорией Дебая—Хюккеля, добавляют­ эмпирические члены степенного ряда:

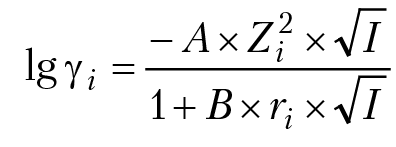
+ CI, где для С рекомендуется значение 0,1 ≈ 0,2.

Таблица 7.1. Ионные радиусы компонентов (ri × 108 [см])

Ионы	ri
Rb+, Cs+, NH4+, Ag+, Tl+	0,25
K+, Cl–, Br–, I–, NO3–	0,30
OH–, F–, HS–, BrO3–, MnO4–	0,35
Na+, HCO3–, H2PO4–, HSO4–, SO42–, SeO42–, CrO42–, PO43–	0,43
Pb2+, CO32–, SO32–	0,45
Sr2+, Ba2+, Ra2+, Cd2+, Hg2+, S2–, WO42–	0,51
Li+, Ca2+, Cu2+, Zn2+, Sn2+, Mn2+, Fe2+, Ni2+, Co2+, Mg2+, Be2+	0,81
H+, Al3+, Cr3+	0,90
Th4+, Zr4+, Ce4+, Sn4+	1,10

7.3. Термодинамическая и концентрационная константы равновесия реакции

В реальных растворах энергия взаимодействия между компонентами раствора сравнима, а иногда и превышает энергию взаимодействия частиц с растворителем. По этой причине, только часть растворенных частиц способна участвовать в химических реакциях. Концентрации этих активных частиц называют активностями компонентов раствора и обозначают а (моль/кг). Если реакция протекает в реальном растворе, bB + rR = wW, то связь между активностями компонентов реакции и концентрациями задаются уравнениями: aB = γB × [B], aR = γR × [R], aW = γW × [W]. [B], [R], W — моляльные концентрации компонентов реакции, γi — коэффициенты активно­сти соответствующих компонентов. Для химического потенциала компонента раствора имеем µ = µ° + RTlna. Для компонента реального газофазного раствора используется понятие летучести (или фугитивности f [бар] ) газа: µ= µ° + RTlnf. Если реакция протекает в реальном растворе, то константа равновесия реакции должна быть записана через активности компонентов реакции и в этом случае константа равновесия реакции называется термодинамической константой равновесия раствора:

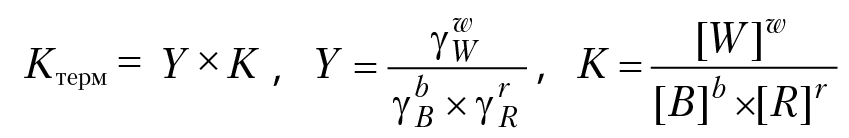
Полученные формулы устанавливают связь между термодинамической и концентрационной константами равновесия реакции. Например, для реакции: Fe2O3 + 3H2O = 2Fe3+ 6OH–; Y = (γFe)2 × (γOH)6. Активности твердой фазы Fe2O3 и воды приняты равными единице. Отметим, что если реакция протекает в реальном растворе, то уравнение Вант-Гоффа должно быть записано через термодинамическую константу равновесия: RTlnKтерм = –∆G(P, T). В этом случае расчет концентрационной константы равновесия необходимо делать с учетом электростатической поправки Y и уравнение Вант-Гоффа примет вид: RTlnK = –[∆G(P, T) + D0], где D0 вычисляем по формуле : D0 = RTlnY.

7.4. Методы прямого учета электростатического взаимодействия ионов при расчете изобарного потенциала

Мы разобрали метод учета взаимодействия между компонентами раствора с помощью понятия об активности компонентов раствора. В данном разделе мы разберем методы оценки взаимодействия компонентов в растворе путем прямого расчета энергии электростатического взаимодействия ионов в растворе. Данный подход к решению задачи позволяет связать константу диссоцииации комплекса (частицы типа NaOH0, FeOH+) с физико-химическими свойствами растворителя. Так как константа диссоциации вычисляется по уравнению Вант-Гоффа RTlnK = –∆G°298, то решение задачи будем искать в виде поправки к изобарному потенциалу реакции, связанную с учетом электростатического взаимодействия ионов:

(7.1)

∆G(P, T) — потенциал Гиббса реакции диссоциации с учетом электростатического взаимодействия ионов, ∆G°R — изобарный потенциал реакции диссоциации, вычисленный в предположении, что реакция протекает в разбавленном растворе; а — сумма ионных радиусов частиц, продуктов диссоциации. Данные для расчета “а” приведены в таблице 7.2: е — заряд электрона, N — число Авагадро. εт,p — диэлектрическая проницаемость воды при соответствующем значении температуры и давления. На основании (10.1) в работе [7] Б. Н. Рыженко предложил формулу для расчета константы диссоциации электролитов, (7.2):

(7.2)

pKst= –lgKst; lgKst = –∆G°298/2,3026 × R × 298,15; e2 × N/(2,3026 × R) = 72 600. Константа 72 600 получается, если сумму ионных радиу­сов a = rk + ra, (rk — ионный радиус катиона, ra — ионный радиус аниона), подставлять в уравнение для pK(Р,Т) в ангстремах: [a] = 10–8 см. Если а = 2,16 × 10–8 , подставлять в уравнение надо число 2,16. Число 0,0128 = 1/ε298 , ε298 — диэлектрическая проницаемость воды при температуре 298 °К. В данной модели учета электростатического взаимодействия ионов мы предполагаем, что имеет место диссоциация симметричного электролита с одним лигандом и рассматривается энергия электростатического взаимодействия j-иона в электрическом поле i-иона. В общем случае необходимо учитывать энергию взаимодействия между катионом и каждым лигандом, а так же энергию отталкивания каждой пары лигандов. При таком анализе электростатического взаимодействия энергия комплекса будет зависить от заряда катиона, числа лигандов и геометрической конфигурации комплекса.

Таблица 7.2. Кристаллохимические радиусы некоторых ионов [12]

ион	ρ	ион	ρ	ион	ρ	ион	ρ
F– Cl– Na+ K+ Mg2+ Ca2+ S2–	1,33 1,81 0,98 1,33 0,78 1,06 1,74	Al3+ Fe2+ Fe3+ Cu+ Ag+ Au+ ClO4–	0,57 0,83 0,67 0,96 1,13 1,37 2,36	Mn2+ Zn2+ OH– HS– NO3– CO3–2 HSO4–	0,91 0,83 1,40 1,95 1,89 1,85 2,06	HCO3– SO4–2 WO4–2 PO4–3 SiO4–4 NH4+ MoO2–	1,63 2,30 2,57 2,38 2,40 1,43 2,54

Геометрическая конфигурация комплекса должна быть такой, чтобы энергия комплекса была минимальной. Это означает, что для комплекса КА2 (К — катион, А2 — два аниона) это линейная структура, А–К–А, КА3 — равносторонний треугольник и т. д. Такое рассмотрение энергии электростатического взаимодействия приводит к поправке расчета Z = |Zi∗Zj|:

(7.3)

где Q = (3 × L2–5 × L+2)/8,

L — число лигандов в комплексе,

zk , za — абсолютные значения зарядов катиона и аниона

ξ — поляризуемость аниона, таблица 7.3.

Подставляя в уравнение для рК вместо |Zi × Zj| значение Z, получим:

(7.4)

Таблица 7.3. Поляризуемость ионов. ξ × 1024 [см3]

анион	Cl–	F–	OH–	CO32–	NO3–	SO42–	Br–	I–
ξ	3,59	4,09	2,04	4,81	4,37	5,83	5,02	7,62
катион	H+	Na+	Mg2+	Ca2+	Cd2+	Ba2+	Fe2+	Al3+
ξ	–0,21	0,08	–0,71	0,28	0,92	1,73	1,13	–1,01

Задача 7.1. Оценить константу диссоциации флюорита при Р = 500 бар и температуре 50 °С с учетом электростатического взаимодействия ионов в растворе и без учета изменения мольного объема раствора.

Решение: значение константы диссоциации CaF2 вычисляем по уравнению (10.4), ∆V = 0. pK°298 = 10,63 (см. задачу 6.3). Вычисляем a = rk + ra = (1,06 + 1,33) × 10–8 см = 2,39 × 10–8см. По уравнениям (10.3) вычисляем эффективный заряд:

Q = (3 × L – 5 × L+2)/8, L = 2 (в молекулу CaF2 два лиганда);

Z = 2 × 2 × 1 –0,5 × 1 + (4,09 × 4)/[2 × 2,39)2] = 4,932;

pK323, 500 = 0,9226 × 10,63 + (4,932/2,39) × 0,2762 = 10,38;

K (323 K, 500 бар) = 4,17 × 10–11;

L (325 K, 500 бар) = 17,04 (мг/кг).