6.1. Растворы. Основные понятия и определения
6.3. Формы нахождения элементов в растворе
6.4. Классификация растворов. Законы Рауля и Генри
6.5. Термодинамика разбавленных растворов
6.6. Уравнение Клапейрона—Клаузиуса. Криоскопия и эбулиоскопия
6.7. Химический потенциал компонента разбавленного раствора
6.9. Анализ равновесия «минерал — раствор»
6.10. Анализ равновесия «газ — раствор»
6.11. Анализ равновесия «газ — раствор — минерал»
6.12. Анализ равновесия «минерал — раствор» в зависимости от рН раствора.
6.1. Растворы. Основные понятия и определения
Растворы — это пример многокомпонентной термодинамической системы переменного состава. В зависимости от фазового состояния растворителя растворы могут быть жидкими, твердыми и газообразными. Твердые растворы особенно часто встречаются при анализе твердых фаз в геологии — это пироксены, плагиоклазы, гранаты, кордиериты и т. д. Грунтовые воды — это пример природных растворов, в которых может быть свыше 100 компонентов. Изучение свойств растворов начнем с анализа жидких растворов. Всякий раствор состоит из растворенных веществ и растворителя, т. е. среды, в которой растворенные частицы равномерно распределяются в виде молекул, ионов, комплексов, ассоциатов и т. д. В качестве растворителя будем подразумевать воду. Важнейшей характеристикой раствора является его состав. Состав может быть выражен безразмерной единицей измерения (мольная доля), а так же через размерные единицы — концентрации.
Определение концентраций раствора.
1. Мольная доля i-компонента в растворе ( xi ) равна отношению числа молей i-компонента к сумме количества молей всех частиц, составляющих раствор:
Пример: вычислить мольную долю ионов Na+ в растворе NaСl в воде, если в одном литре воды было растворено 58,45 г соли при 25 °С.
Решение: 58,45 г NaСl — это один моль вещества. При растворении одного моля NaСl в раствор перейдет один моль ионов Na+ и один моль ионов Сl–, всего образуется в растворе два моля частиц растворенного вещества. В одном литре воды при 25 °С содержится n = 1000/18,016 = 55,51 моль. Следовательно, всего в растворе будет 1 + 1 + 55,51 = 57,51 моль частиц. Мольная доля ионов Na+ в растворе будет равна: х(Na+) = 1/57,51 = 1,73 × 10–2 . Мольная доля растворителя в растворе будет равна: x(H2O) = 55,51/57,51 = 0,965.
2. Молярная концентрация i-компонента в растворе (ci), или молярность — число молей i-компонента в одном литре раствора.
3. Моляльная концентрация i-компонента в растворе (mi) или моляльность — число молей i-компонента в одном килограмме растворителя.
С термодинамической точки зрения растворы делятся на идеальные, разбавленные и реальные. Определение данной классификации растворов будет сделано в последующих разделах лекций.
При растворении в воде электролиты (NaСl, KСl, Na2СO3 и т. д.) диссоциируют (распадаются ) на положительно заряженные ионы (катионы , H+, Сa2+ , Mg2+ ) и отрицательно заряженные ионы (анионы, OH–, SO42– , Сl–, СO32– ) . Реакции диссоциации записываются в виде уравнения диссоциации:
MgСl2 = Mg2+ 2Сl–, СaСO3 = Сa2+ СО32–
Растворение кристаллических веществ всегда начинается со стадии диссоциации — выхода в раствор ионов, которые входят в состав кристаллической решетки. Попадая в воду, ионы подвергаются гидратации: каждый ион окружается молекулами воды. Диссоциация может наблюдаться и при растворении газов: например, растворение аммиака:
NH3 + H2O = NH4+ OH–
Может наблюдаться и диссоциация ассоциатов или комплексов:
H2СO30 = HСO3– + H+
Al(OH)30 = Al(OH)2+ OH–
Не всегда уравнения диссоциации имеют простой вид. Например, при записи реакции диссоциации микроклина K(AlSi3O8) необходимо проверять условие электронейтральности и баланс по массе:
K(AlSi3O8) + 4H2O = K+ Al3+ 3SiO44– + 8H+
Отметим, что в составе силикатов кремний находится в кристаллической решетке в виде иона SiO44–.
Гидролиз. При химической реакции воды с частицами растворенного вещества они (частицы) подвергаются гидролизу:
СO32– + H2O = HСO3– + OH–; реакции.
NH4+ H2O = NH4OHо + H+; гидролиза.
Форма записи реакций гидролиза: реакцию СO32– + H2O = HСO3– + OH– можно записать в виде уравнения: СО32– + Н+ = НСО3–, это равнозначная форма записи реакции гидролиза карбонатного иона, просто надо иметь в виду, что вода всегда находится в равновесии с продуктами диссоциации: Н2О = Н+ ОН–, причем при температуре раствора Т = 298 °К [H+]∗[OH–] = 10–14. Если один из компонентов реакции диссоциации воды вступает в реакцию, равновесие нарушается и новая порция воды диссоциирует, т. е. происходит изменение количества воды в растворе. При протекании реакций гидролиза вода (или продукты ее электролитической диссоциации Н+ или ОН–) является компонентами химической реакции. Растворение галита NaCl в воде: NaCl = Na+ Cl– не является реакцией гидролиза минерала, так как вода в данном случае является средой, в которой распределяются продукты растворения минерала. В данном случае имеет место гидратация ионов, т. е. окружение ионов молекулами воды. Реакции гидролиза играют очень важную роль в теории растворов. Как правило, они лежат в основе процессов, в результате которых устанавливается равновесие в растворах. Ранее, рассматривая процесс растворения аммиака NH3 + H2O = NH4+ OH–, мы назвали данную реакцию реакцией диссоциации аммиака, хотя ее можно трактовать и как реакцию гидролиза аммиака. Отметим, что некоторые ионы не подвергаются гидролизу, например: Nа+, K+, Сl–, I– и т. д. Этому есть простое объяснение. Например, в результате гидролиза иона натрия Na+ в продуктах реакции мы должны записать щелочь NaOH, которая мгновенно диссоциирует на ионы натрия и гидроксил:
Na+ H2O = NaOH + Н+ = Na+ OH– + H+ = Na+ H2O
Окислительно-восстановительные реакции. Процессы горения, фотосинтез, дыхание человека и т. д. — все это окислительно-восстановительные реакции. В результате протекания окислительно-восстановительных реакций происходит передача заряда от одной частицы другой: например, при пропускании хлора (газ) через бромную воду происходит окисление иона Br– (отдача электрона) и восстановление хлора до иона Сl–: 2Br– + Сl2(газ) = Br2(газ) + 2Сl–.
6.3. Формы нахождения элементов в растворе
В результате растворения вещества и протекания реакций гидролиза, комплексообразования, и т. д. элементы, которые образуют вещество и которые перешли в раствор, будут находиться в растворе в самых разных формах: например, алюминий может находиться в воде в виде иона Al3+ , ассоциатов: Al(OH)2+ , Al(OH)2+ , Al(OH)30, комплекса: Al(OH)4–. Кальций в воде можно обнаружить в виде ионов Са2+ , ассоциатов Са(OH)+ , Сa(HСOз)+ и т. д. Углерод в растворах находится в виде частиц СО32–, HСOз–, H2СO30 . Равновесие между этими частицами в растворе устанавливается в результате протекания реакций гидролиза: СO32– + H2О → HСO3– + ОН–; HСO3– + H2О → H2СO30 + ОН–. Огромное влияние на формы нахождения элементов в растворе оказывает концентрация ионов водорода в растворе [H+]. Концентрация ионов водорода зависит от ионного произведения воды (константы диссоциации воды). При 25 °С константа диссоциации воды [H+]∗[OH–] = 10–14. Если в растворе [H+] > 10–7, такой раствор называют кислым, если [H+]<10–7 раствор щелочной, при [H+] = 10–7 — раствор нейтральный (Т = 25 °С).
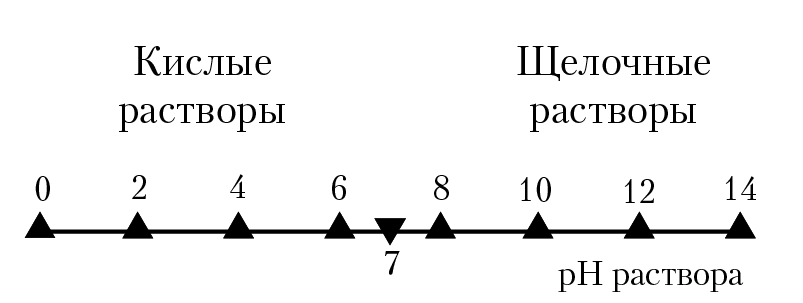
Рис. 6.1. Кислотность раствора
При анализе кислотности раствора (зависимости свойств раствора от концентрации ионов водорода в растворе) удобно пользоваться понятием рН раствора. По определению, pH = – lg[H+]. На рисунке 6.1 кислотность раствора выражена через рН раствора. Мы уже отмечали, что формы нахождения элементов в растворе в значительной степени определяются реакциями гидролиза, В свою очередь, в результате реакций гидролиза изменяется рН раствора, что приводит к значительной зависимости форм нахождения элементов в растворе от рН раствора. В таблице 6.1 и на диаграмме приведены результаты расчета р[Са] = –lg[m], где [m](моль/кг) — концентрация частицы, в состав которой входит кальций , в зависимости от рН раствора. Расчеты выполнены по программе Ground для персональных ЭВМ (кафедра химии, 1985 г.), для концентрации элемента 10–3(моль/кг) и давлении углекислого газа 3 × 10–4 бара; температура раствора 25 °С. Алгоритм решения задачи разбирается в девятой главе лекций.
Таблица 6.1. Результаты расчета форм нахождения кальция в растворе
|
pH |
pH 3 |
pH 7 |
pH 12 |
|
Ca2+ |
4,36 |
4,15 |
5,48 |
|
Ca(OH)+ |
9,85 |
5,65 |
6,33 |
|
Ca(HCO3)+ |
7,19 |
7,34 |
3,66 |
|
CaCO30 |
12,52 |
4,35 |
4,15 |
Задача 6.1. Рассчитать формы нахождения алюминия в зависимости от рН раствора.
Решение: считаем, что алюминий в растворе можно встретить в виде частиц Al3+, Al(OH)2+, ... Al(OH)4–. Равновесие между формами нахождения алюминия в растворе устанавливается в результате протекания реакций гидролиза. Вычислим, при каком значении рН раствора будет иметь место равенство концентраций Al3+ и Al(OH)2+.
Al3+ H2O = Al(OH)2+ H+ (уравнение 1)
Запишем выражение для константы равновесия реакции:
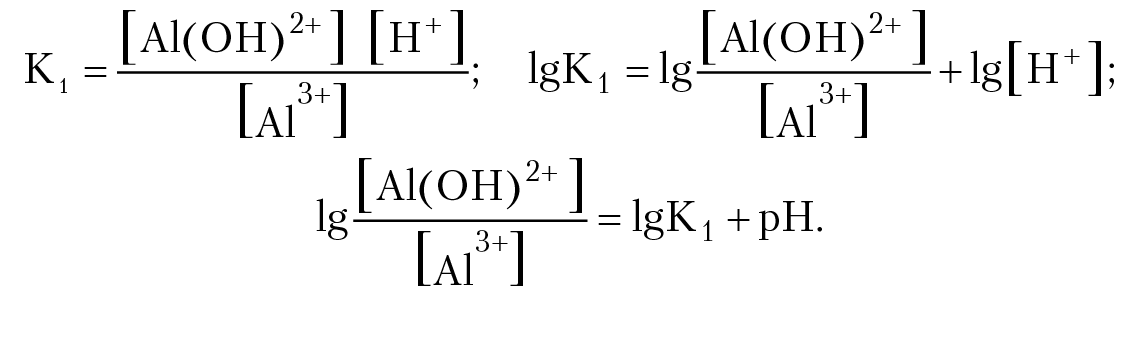
(–lg[H+] = pH). Таким образом, если концентрации частиц Al3+ и Al(OH)2+ равны (логарифм отношения концентраций равен нулю) тогда рН = –lgК1.
Значение константы равновесия вычислим по уравнению Вант-Гоффа: RTlgK1 = –(∆G°298)1)/2,3; (∆G°298)1= 21429(Дж/моль); lgK1 = –3,75; Мы получили, что [Al3+] = [Al(OH)2+], если pH = –lgK1 = 3,75.
Используя уравнение 2 вычислим, при каком значении рН раствора концентрации частиц [Al(OH)2+] и [Al(OH)2+} будут равны;
Al(OH)2+ H2O = Al(OH)2+ H+ (уравнение 2)
Запишем выражение для константы равновесия реакции и прологарифмируем:
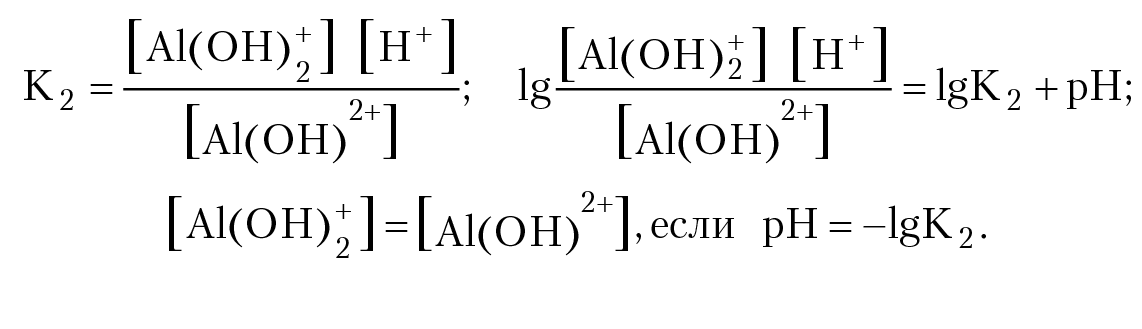
Значение константы равновесия вычислим по уравнению Вант-Гоффа:
RTlgK2 = –(∆G°298)2)/2,3; (∆G°298)2 = 31 002 (Дж/моль)
lgK2 = –5,43
[Al(OH)2+] = [Al(OH)2+], если рН = 5,43
Используя уравнение 3, вычисляем значение рН раствора, при котором концентрация частиц Al(OH)2+ равна концентрации частицы Al(OH)30:
Al(OH)2+ H2O = Al(OH)30+ H+ (уравнение 3)
[Al(OH)2+] = [Al(OH)30], если рН = 5,58
Используя уравнение 4, вычисляем значение рН раствора, при котором концентрация частиц Al(OH)30 равна концентрации частиц Al(OH)4–:
Al(OH)30 + H2O = Al(OH)4– + H+ (уравнение 4)
[Al(OH)30] = [Al(OH)4–], если рН = 7,42
Результаты расчета наносим на диаграмму, рис. 6.2. Разметку диаграммы выполняем на основании принципа Ле-Шателье: в нашем случае, при увеличении рН раствора (т. е. при уменьшении концентрации ионов водорода, [Н+] ) равновесие реакций 1–4 сдвигается вправо, т. е. вправо от равновесного значения рН возрастает концентрация частицы, которая записана справа в уравнениях 1–4.
Анализ рис. 6.2. В кислых растворах, до рН = 3,75 преобладающей формой алюминия в растворе будет ион Al3+. По мере возрастания рН концентрация Al3+ начнет уменьшаться, а концентрация частицы Al(OH)2+ возрастать и при рН = 3,75 [Al3+] = [Al(OH)2+]; при рН > 3,75 концентрация иона Al3+ продолжит резко уменьшаться, менее заметно начнет уменьшаться концентрация частицы Al(OH)2+ и начнет возрастать концентрация частицы Al(OH)2+; при рН = 5,43 концентрация частиц Al(OH)2+ и Al(OH)2+ будут равны. Продолжая анализ рис. 6.2 мы получим информацию о концентрации частиц Al(OH)30, Al(OH)4–. Отметим, что в кислых растворах алюминий в растворе присутствует в виде «простого» иона Al3+, в щелочных растворах, при рН > 7,42 — в форме Al(OH)4–.
6.4. Классификация растворов. Законы Рауля и Генри
Термодинамика растворов должна решать одну из основных проблем теории растворов — предсказывать свойства раствора на основании информации о компонентах, при участии которых происходит образование раствора. Раствор — это термодинамическая система, в которой имеют место самые разные по энергии взаимодействия между компонентами. Характер и величина взаимодействия между компонентами и лежит в основе термодинамической классификации растворов. Растворы, в которых энергия взаимодействия между всеми компонентами предполагается одинаковой, называются идеальными растворами. Растворы, в которых частицы растворенных веществ окружены молекулами растворителя и для которых энергия взаимодействия между собой намного меньше энергии взаимодействия с молекулами растворителя, называются разбавленными растворами. Природные растворы в основной своей массе — это разбавленные растворы. Растворы, в которых энергия взаимодействия между частицами растворенных веществ сравнима или превышает энергию взаимодействия с молекулами растворителя, называются реальными растворами. Кроме термодинамической классификации растворов в гидрогеохимии природные воды делят в зависимости от величины минерализации на следующие группы: пресные воды (до 1 г/кг), солоноватые (от 1 до 25 г/кг), соленые (от 25 до 50 г/кг) и рассолы (выше 50 г/кг).
Идеальные растворы. Идеальные растворы образуются без теплового эффекта и без изменения объема. Так как энтальпия образования идеального раствора равна нулю, для идеального раствора ∆G = –T∆S, т. е. тенденция к образованию идеального раствора определяется только изменением энтропии системы при образовании раствора. Покажем, что изменение энтропии при образовании раствора больше нуля. Действительно, изменение энтропии при образовании раствора равно ∆S =–R(x1lnx1+x2lnx2), R = 8,31 Дж/(моль×К), х1 — мольная доля растворенного вещества, х2 — мольная доля растворителя. Так как х2 = 1 – х1 (бинарный раствор), то ∆S =–R[x1lnx1 + (1 – x1) × ln(1 – x1)], ∆G = RT[x1lnx1+(1 – x1) × ln (1 – x1)]. Так как при любых концентрациях раствора х1 < 1, получаем, что изобарный потенциал образования ∆G идеального раствора всегда отрицателен, а энтропия ∆S образования идеального раствора — положительна. Для всех компонентов идеального раствора выполняется закон Рауля: при равновесии давление паров i-компонента над раствором пропорционально мольной доле этого компонента в растворе: Рi = рi° × хi . Рi — парциальное давление паров i-го компонента над раствором; рi° — давление паров i-го компонента над жидкой фазой этого компонента, т. е. над раствором, состоящим только из этого компонента; xi — мольная доля i-го компонента в растворе. Для бинарного раствора общее давление пара над раствором будет равно Робщ. = р1 + р2 где р1 и р2 — парциальные давления пара растворенного вещества и растворителя соответственно. На основании закона Рауля имеем: р1 = р10 × х1 , р2 = р20 × (1 — x1). Закон Рауля позволяет установить вид зависимости химического потенциала компонента раствора от его концентрации (мольной доли): µi = µ*i + RTln(хi); µi — химический потенциал компонента идеального раствора, если его мольная доля в растворе равняется хi, µ*i — химический потенциал i-компонента в растворе, полностью состоящего из данного компонента. В частности, для компонента идеального газофазного раствора, который подчиняется законам Дальтона и Клапейрона–Менделеева, выражение для химического потенциала можно записать в виде уравнения: µi = µ0i + RTlnpi; µ0i — стандартный химический потенциал компонента. µ0i — потенциал i-компонента при его парциальном давлении в системе 1 бар, pi(бар) — парциальное давление компонента в системе. В этом разделе мы познакомились с особой [воображаемой] термодинамической системой — идеальным раствором. В идеальном растворе все компоненты равноправны — и частицы растворенных веществ и молекулы растворителя. Мы сформулировали законы, которым подчиняется наш раствор, и описали свойства этого раствора. Все это нам надо для того, чтобы решить основную задачу термодинамической теории природных растворов — предсказать направление процессов в растворе и вычислить параметры равновесного состояния раствора. Ввиду сложного характера взаимодействия компонентов в растворе, решение этой задачи в общем виде на сегодня не найдено. Поэтому, используя результаты, полученные для идеального раствора, построим термодинамическую модель разбавленного раствора.
6.5. Термодинамика разбавленных растворов
Разбавленные растворы мы определили как растворы, в которых частицы растворенного вещества отделены друг от друга большим числом молекул растворителя. В этом случае имеет место только взаимодействие между растворенными частицами и молекулами растворителя, но не между частицами растворенного вещества. Примером разбавленного раствора можно считать растворы газов в воде, многие природные растворы. В отличие от идеальных растворов, для разбавленных растворов закон Рауля выполняется только для растворителя, т. е. воды. В разбавленных растворах концентрация растворенного газа подчиняется закону Генри: отношение давления газа над раствором к его концентрации в растворе есть величина постоянная и зависит только от температуры. Закон Генри: Р/m = Г; Р — давление газа над раствором, m [моль/кг] — концентрация газа в растворе, Г — постоянная Генри. При изучении фазовых равновесий мы еще вернемся к закону Генри.
6.6. Уравнение Клапейрона—Клаузиуса. Криоскопия и эбулиоскопия
Для идеального и разбавленного растворов давление насыщенного пара над раствором при фиксированной температуре зависит только от мольной доли растворителя, закон Рауля: Р = Р0 × х0; Р0 — давление насыщенного пара над чистым растворителем, х0 — мольная доля растворителя. Температурная зависимость давления насыщенного пара растворителя над раствором носит более сложный характер (уравнение Клапейрона — Клаузиуса). Действительно, изменение температуры раствора на dТ градусов приводит к изменению давления насыщенного пара на dP (бар); эти изменения связаны с изменением изобарного потенциала фазового перехода соотношением: d∆G = ∆VdP – ∆SdT (выражение для полного дифференциала изобарного потенциала процесса). При квазиравновесном процессе, d∆G ≈ 0, ∆VdP = ∆SdT, dP/dT = ∆S/∆V, уравнение Клапейрона—Клаузиуса (К–К); ∆S — энтропия фазового перехода жидкость — пар. ∆S = λ/T0, λ (Дж/моль) — теплота фазового перехода, Т0 — температура фазового перехода. Для воды, λ ≈ 41 кДж/моль, Т0 = 373К ; ∆V = V2 – V1 (V1 — объем одного моля жидкости, V2 — объем одного моля пара. Для воды при t°C < 100°, V2 >> V1, ∆V ≈ V2). Считая пар идеальным газом, PV = RT для одного моля, ∆V = RT/P. Подставляя полученные соотношения в уравнение К–К, получим:
в интегральной форме
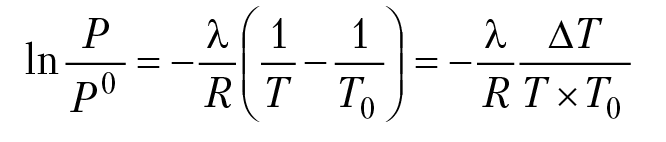
Р0 — давление насыщенного пара растворителя над раствором при Т = Т0, ∆T = T0 – T. Для малых значений ΔТ, Т × Т0 ≈ Т02;
Если раствор разбавленный, то для растворителя выполняется закон Рауля Р/Р0 = (1 – х), где х — мольная доля растворенного вещества и при малых значениях х ln(P/P0) = ln(1–x) ≈ – x. Заменяя мольную долю растворенного вещества на моляльную концентрацию х = mM/1000, m (моль/кг) — моляльная концентрация раствора, М — относительная молекулярная масса растворенного вещества, получим окончательно: ∆T = E × m,
[град/моль] — эбулиоскопическая постоянная растворителя, Т0 [К] — температура кипения растворителя. Полученная формула позволяет вычислить изменение температуры кипения раствора в зависимости от мольной доли растворенного вещества. В таблице 6.2 приведены значения эбулиоскопических постоянных, полученных в результате расчета Е* и эксперимента Е. Понижение температуры замерзания раствора связано с моляльной концентрацией соотношением ∆T = Ef × m, где Ef (моль/град) — криоскопическая постоянная;
T0f [K] — температура замерзания растворителя, ηf — моляльная теплота плавления растворителя. Метод измерения повышения температуры кипения, называется эбулиоскопией и используется для определения молекулярной массы растворенного вещества. Аналогично, метод измерения понижения температуры замерзания называется криоскопией.
Таблица. 6.2. Криоскопические (Ef) и эбуллиоскопические (Е) постоянные
|
Растворитель |
Ef* |
Ef |
E* |
E |
|
Вода |
1,862 |
1,861 |
0,514 |
0,52 |
|
Этиловый спирт |
1,21 |
1,21 |
||
|
Бензол |
7,81 |
7,80 |
2,63 |
2,63 |
|
CCl4 |
5,25 |
5,06 |
6.7. Химический потенциал компонента разбавленного раствора
Если ∆G (Дж/моль) — изобарный потенциал образования раствора, тогда, по определению, химическим потенциалом компонента раствора называется частная производная от потенциала раствора по количеству данного компонента в растворе: µ = (d[∆G]/dn)pт. Из данного определения следует, что мы можем оценить, как измениться потенциал раствора, если в раствор добавить n(моль) вещества с химическим потенциалом µ: d(∆G) = µ*dn. Можно показать, что µ = µ° + RTln[m], где µ° — стандартный химический потенциал компонента в растворе (потенциал при давлении в системе 1 бар и температуре 298 °К), m (моль/кг) — моляльная концентрация компонента в растворе. Первое слагаемое характеризует термодинамические свойства данного компонента, второе слагаемое — энергию взаимодействия компонента с раствором. Например, химический потенциал иона Са2+ в растворе при температуре 298 °С и концентрации иона 6 × 10–5(моль/кг) равен: µ = µ0 + RTln[Ca2+] = –552 180 + 2478,94(–9,72) = –576 278 (Дж/моль). В разбавленных растворах относительная концентрация воды стремится к единице, поэтому химический потенциал воды при стандартных условиях есть величина постоянная и равна µ0 (H2O) = –236 950 (Дж/моль).
6.8. Анализ гетерогенного равновесия при стандартной температуре в рамках модели разбавленного раствора при 298 °К
Гетерогенное равновесие в растворах устанавливается при образовании насыщенных растворов при растворении газов и твердых тел. В главе 3 мы получили уравнения Вант-Гоффа, с помощью которых можно провести анализ равновесия в системе. Посмотрим на примере задачи 6.2 как «работают» полученные уравнения.
Задача 6.2. Вывести закон Генри.
Закон Генри утверждает, что отношение давления газа над раствором к концентрации газа в растворе есть величина постоянная, т. е. Р / m = Г (константа Генри). С термодинамической точки зрения, формулировка закона Генри соответствует равновесию между газом и раствором. Данное равновесие можно записать в виде уравнения: Nгаз = N0. Nгаз — молекулы газа, N0 — гидратированные молекулы газа. Так как характеристикой газовой фазы является величина парциального давления газа, характеристикой газа в растворе — концентрация гидратированных молекул газа в растворе, выражение для константы равновесия реакции Nгаз = N0 будет иметь вид: К = [N0]/PN, т. е. Г = 1/К. Константу равновесия реакции вычислим по уравнению Вант-Гоффа: К = ехр(–∆G°298/RT). Так как правая часть равенства зависит только от химической природы газа и температуры, получим закон Генри: P/m = const.
6.9. Анализ равновесия «минерал — раствор»
Гетерогенное равновесие между твердой фазой и раствором наступает в момент образования насыщенного раствора. Характерной особенностью такого равновесия является обязательное присутствие в растворе твердой фазы. В результате анализа равновесия «минерал — раствор» можно вычислить, сколько растворится минерала в заданном объеме растворителя, вычислить концентрацию компонентов насыщенного раствора, оценить влияние различных факторов на растворимость вещества. Получить необходимую информацию в полном объеме «на руках», без использования вычислительной техники, крайне сложно. Но надо уметь делать оценки. Например, оценим растворимость флюоресцита, CeF3.
Задача 6.3. Оценить растворимость флюоресцита, считая, что при равновесии образуется разбавленный раствор.
Решение: оценить растворимость минерала можно из анализа реакции диссоциации вещества, придерживаясь следующей схемы расчета:
1) запишем реакцию диссоциации минерала: СeF3 = Сe3+ 3F–;
2) вычислим константу равновесия реакции диссоциации: K = [Се3+] × [F–]3.
Пусть в 1 кг воды растворится х (моль) минерала. Тогда [Ce3+] = x, [F–] = 3x. Растворимость минерала и константа равновесия реакции будут связаны соотношением: K = x × (3x)3 = 27x4. С другой стороны, на основании уравнения Вант-Гоффа, для константы равновесия реакции можно записать: RTlnK = –∆G°298, где ∆G°298 — стандартный изобарный потенциал реакции диссоциации флюоресцита. Используя справочные данные, вычислим ∆G°298 = +85486 (Дж/моль), а по уравнению Вант-Гоффа — константу равновесия реакции, К = 1,52 × 0–15. Так как изобарный потенциал реакции диссоциации вещества оказался сильно положительный, это указывает на то, что вещество плохо растворяется. Это видно и из значения константы равновесия реакции. Пусть L(мг/л) — растворимость минерала. Так как
для растворимости минерала L получим: L = 1000 × М × x = 17 (мг/кг), М — молекулярная масса флюоресцита. Полученный результат хорошо совпадает с экспериментальными данными (17,4 мг/л). Это произошло по той причине, что при растворении флюоресцита вклад реакций гидролиза и комплексообразования незначительный и данные реакции в схеме растворения минерала можно не принимать во внимание.
Совсем другая ситуация будет при анализе растворения, например, карбонатных пород. Так, если при растворении витерита считать, что процесс заканчивается на стадии диссоциации твердой фазы, ВаСО3 = Ва2+ СО32– получим, что растворимость витерита L = 9,4 (мг/л). Если принять во внимание реакцию гидролиза карбонатного иона и считать, что процесс растворения витерита надо записать в виде набора реакций:
ВаСО3 = Ва2+ СО32–, СО32– + Н2О = НСО– + ОН–;
Н2О = Н+ ОН–,
то для растворимости минерала получим: L = 46,67 (мг/л). Lэксп = 48,96 (мг/л). Приведенный пример показывает, что схема решения задачи сильно зависит от конкретной системы. Конечно, чем большее количество реакций мы будем принимать во внимание при анализе процесса растворения вещества, тем точнее ответ. Но нельзя забывать, что увеличение числа реакций приводит к значительным математическим проблемам при решении задачи. Например, при решении задачи о растворимости минерала с учетом трех реакций, так как это сделано для витерита, для отысканния х необходимо решить уравнение пятой степени, причем среди коэффициентов уравнения есть числа порядка 10–8, 10–12. Решить такую задачу «на руках» просто невозможно. Подробно данная проблема обсуждается в методическом пособии [12].
Отметим, в химии константа равновесия реакции диссоциации плохо растворимого вещества называется произведением растворимости вещества ПР. Например, для CeF3 ПР = [Сe3+][F—]3 и ПР = К = 1,52 × 10–15 (задача 6.3).
Задача 6.4. Вычислить произведение растворимости для флюорита CaF2.
Решение: реакция диссоциации флюорита: CaF2 = Ca+2 + 2F–. Проиведение растворимости ПР = [Ca2+][F—]2. Вычислим константу равновесия реакции диссоциации:
lgK = –10,63, K = 5,78 × 10–12, ПР = 5,78 × 10–12.
6.10. Анализ равновесия «газ — раствор»
При анализе гетерогенного равновесия газ — раствор необходимо принимать во внимание два крайних случая:
1) отсутствие химического взаимодействия растворенного газа с раствором;
2) активное химическое взаимодействие молекул растворенного газа с раствором.
Первый тип растворения газа имеет место при растворении азота, водорода, кислорода, благородных газов. В этом случае процесс растворения газа можно описать одной реакцией. Например, для азота: N2газ = N2°. Вычислим концентрацию газа в растворе [N2°] в данном случае несложно. Действительно, пусть давление газа над раствором p(N2) = 0,76 бар (поверхность Земли). Тогда константа равновесия реакции К = [N2°]/p(N2), и для концентрации газа в растворе, получим: [N2°] = p(N2) × K, где К — константа равновесия реакции: N2газ = N2о. Константу равновесия реакции К вычисляем по уравнению Вант-Гоффа: К = exp(–∆G°298/RT). Так как ∆G°298 = 18 140(Дж/моль), К = 6,64 × 10–4 и для концентрации газа в растворе, получим: [N20] = 5 × 10–4 (моль/кг).
В случае активного химического взаимодействия молекул растворяемого газа с водой при растворении газа, необходимо принимать во внимание химические реакции, которые протекают при растворении газа. Например, при анализе равновесия «двуокись углерода — раствор» надо записать набор реакций:
СО2газ + Н2О = Н2СО30
Н2СО30 = НСО3– + Н+
НСО3– = СО32– + Н+
Концентрация растворенного газа будет равна сумме концентраций частиц, в состав которых входит углерод: [m](моль/кг) = [Н2СО30] + [НСО3—] + [СО32—], количество растворенного газа L[мг/кг] = 44 × 1000 × m. Подробно математический алгоритм решения данной и ей подобных задач обсуждается в [9].
Набор реакций, который описывает процесс растворения газа, зависит от физико-химических свойств газа и, естественно, невозможно предложить универсальную схему растворения газа. Но для растворения таких газов, как сероводород, H2S, серный газ SO3 и им подобные, схема растворения газа такая же, как и для углекислого газа.
6.11. Анализ равновесия «газ — раствор — минерал»
При анализе гетерогенного равновесия «газ — раствор — минерал» особое внимание необходимо уделить вопросу о взаимном влиянии на параметры равновесного состояния химической природы газа и твердой фазы. Отметим, что равновесному состоянию анализируемой системы соответствует насыщенный раствор, т. е. наша система трехфазная — раствор, в растворе присутствует твердая фаза, а над раствором — газовая фаза. Если в процессе растворения газа и твердой фазы в растворе будут образовываться одинаковые частицы, то взаимное влияние на растворение газа и твердой фазы будет очень велико. Например, на растворение углекислого газа СО2 большое влияние окажет присутствие в растворе карбонатных пород (пород, в состав которых входит группа СО32—). Будет правильным и прогноз: растворение карбонатных пород будет зависеть от давления углекислого газа над раствором. С другой стороны, не следует ожидать значительного влияния углекислого газа на растворение силикатных пород. В качестве примера сравним параметры насыщенных растворов:
1) углекислый газ + раствор;
2) кальцит + раствор;
3) СО2 + СаСО3 + раствор.
1. Считаем, что равновесие углекислый газ + раствор устанавливается в результате протекания реакций:
СО2газ + Н2О = Н2СО30; Н2СО30 = НСО3— + Н+; НСО3— = СО32— + Н+.
При растворении кальцита принимаем во внимание реакции:
1. СаСО3 = Са2+ СО32–;
2. Са2+ Н2О = СаОН+ Н+;
3. Са2+ СО32— = СаСО30;
4. СО32– + Н2О = НСО3–;
5. НСО3– + Н2О = Н2СО30.
Примечание: ионная сила раствора I = 1/2Σmk × zk, mk — моляльная концентрация k-компонента раствора, zk — заряд k компонента раствора. При растворении кальцита в присутствии углекислого газа принимаем во внимание реакции:
1. СаСО3 = Са2+ СО32– ;
2. Са2+ Н2О = СаОН+ Н+ ;
3. Са2+ СО32– = СаСО30;
4. СО2газ + Н2О = Н2СО30 ;
5. Н2СО30 = НСО3– + Н+ ;
6. НСО3– = СО32– + Н+.
Таблица 6.3. Результаты расчета компонентного состава раствора.
Давление газа СО2 над раствором p = 3 × 10–4 бара. рН раствора 5,672;
ионная сила раствора I = 2 × 10–5. Растворимость газа 3,13 × 10–5 (моль/кг)
|
Компонент |
Концентрация, [моль/кг] |
|
Н2СО30 |
1,02 × 10–5 |
|
НСО3– |
2,11 × 10–5 |
|
СО32– |
4,69 × 10–11 |
Таблица 6.4. Результаты расчета растворения кальцита в отсутствии углекислого газа.
рН раствора 9,907, ионная сила раствора I = 4 × 10–4.
Кальцита растворилось 1,22 × 10–4 (моль/кг).
Концентрации компонентов раствора (моль/кг)
|
Са2+ |
СаОН+ |
СаСО30 |
Н2СО30 |
НСО3– |
СО32– |
|
1,15 × 10–4 |
1,32 × 10–7 |
6,11 × 10–6 |
2,38 × 10–8 |
8,29 × 10–5 |
3,19 × 10–5 |
Таблица 6.5. Результаты расчета гетерогенного равновесия
кальцит + СО2 + раствор. Давление газа над раствором p(СО2) = 3 × 10–4 бар;
рН = 8,29. Растворимость газа 9,23 × 10–4 (моль/кг).
Кальцита растворилось 4,57 × 10–4 (моль/кг).
Концентрации компонентов раствора (моль/кг)
|
Са2+ |
СаОН+ |
СаСО30 |
Н2СО30 |
НСО3– |
СО32– |
|
4,49 × 10–4 |
1,24 × 10–7 |
6,11 × 10–6 |
1,02 × 10–8 |
8,79 × 10–4 |
8,16 × 10–6 |
Анализ таблиц 6.3–6.5 позволяет сделать вывод о взаимном влиянии на растворимость газа, присутствие минерала и наоборот. В присутствии газа кальцита растворилось 4,57 × 10–4 (моль/кг), в отсутствии газа в 3,8 раза меньше. Присутствие кальцита увеличило растворимость газа почти в 100 раз. Как правило, это влияние особенно заметно, когда в продуктах растворения веществ присутствуют одноименные частицы и когда сильно изменяется рН раствора. Для кальцита рН раствора уменьшается в присутствии углекислого газа, что приводит к возрастанию растворимости минерала. Для углекислого газа присутствие минерала увеличивает рН раствора (рН = 5,67 в отсутствии минерала в растворе и 8,29 в присутствии минерала).
Как известно, растворимость углекислого газа возрастает в щелочных растворах, что и получено в результате расчета.
Примечание. Расчеты компонентного состава насыщенных растворов выполнены с использованием программы «MATRIX» для персональных компьютеров. (Умрихин В. А., 1985 г.)
6.12. Анализ равновесия «минерал — раствор» в зависимости от рН раствора.
Если при растворении вещества образуются ионы водорода Н+ или гидроксила ОН–, то данный процесс будет зависеть от рН раствора. Например, растворение гидрокомлексов (вещества, с общей химической формулой Rr(OH)n), сильно зависит от рН раствора. Это видно из анализа набора реакций, которые описывают процесс растворения гидрокомплексов:
1. Sn(OH)2 = Sn2+ 2OH — ;
2. Sn2+ H2O = Sn(OH)+ H+;
3. Sn(OH)+ H2O = Sn(OH)20 + H+ ;
4. Sn(OH)20 + H2O = Sn(OH)3– + H+.
Так как в результате реакций гидролиза (2–4) накапливаются протоны (Н+), то будет понижаться рН раствора, а растворимость соли будет возрастать в кислых растворах. Растворимость вещества можно представить в виде зависимости lg[конц.] = f(pH). Если построить график соответствующей зависимости, то получим диаграмму полей устойчивости вещества в координатах [растворимость]/[рН].
Задача 6.5. Построить поле устойчивости Sn(OH)2 в координатах lg[X]/[pH], где [X] — моляльная концентрация олова в растворе.
Решение: схема решения задачи может быть следующей: считаем, что при растворении гидроксида олова в растворе образуются частицы Sn2+, Sn(OH)+, Sn(OH)20, Sn(OH)3– в результате протекания реакций:
1. Sn(OH)2 + 2H+ = Sn2+ 2H2O; ∆G°298 = –9770 (Дж/моль); RTlgK = –∆G°298 /2,301; lgK = 1,712. K = [Sn2+]/[H+]2,
lgK = lg[Sn2+] – 2lg[H+] = lg[Sn2+] + 2pH;
1. lg[Sn2+] = 1,712 – 2pH
2. Sn(OH)2 + H+ = Sn(OH)+ H2O. ∆G°298 = 2420 (Дж/моль);
2. lg[Sn(OH)+] = –0,424 – pH
3. Sn(OH)2 = Sn(OH)2°. ∆G°298 = 28480 (Дж/моль).
3. lg[Sn(OH)20] = –4,990;
4. Sn(OH)2 + H2O = Sn(OH)3– + H+. ∆G°298 = 82 960 (Дж/моль);
4. lg[Sn(OH)3–] = –14,534 + pH.
Будем откладывать по оси OY десятичный логарифм концентрации частиц, в состав которых входит олово, по оси ОХ — рН раствора. В данных координатах построим графики функций 1–4. Отметим точки пересечения прямых [1,2], точка В [2, 3], точка С [3, 4], точка D. После соединения этих линий получим «полуостров» растворимости Sn(OH)2: ABCDE: выше линий равновесия, раствор пересыщен (идет образование твердой фазы из раствора), а ниже — недосыщен, твердая фаза будет растворяться. На рисунке 6.3 приведена зависимость растворимости гидроксида олова от рН раствора.

Рис. 6.3. Поле устойчивости Sn(OH)2

