Физическая химия

5.1. Общая характеристика равновесного состояния

5.2. Константа равновесия химической реакции. Изотерма Вант-Гоффа

5.3. Оценка температурного интервала устойчивости минералов

5.4. Поля устойчивости минералов. Строение Земли

5.5. Поля устойчивости минералов в присутствии углекислотного и флюида

5.6. Термодинамическое описание геотермометров и геобарометров

5.1. Общая характеристика равновесного состояния

Определим равновесное состояние системы, как состояние системы, в которой скорость химической реакции в прямом направлении равна скорости реакции в обратном направлении. Такому состоянию системы соответствуют вполне определенные значения параметров состояния системы (мы их будем называть равновесные параметры системы). При равновесии изобарные потенциалы всех реакций в системе должны равняться нулю: ∆Gi = 0. Одной из важнейших характеристик равновесного состояния системы является константа равновесия реакции. Определим понятие константы равновесия реакции. Пусть в результате протекания реакции aA + bB = dD в системе установится равновесие. Тогда константа равновесия

В числитель и в знаменатель дроби записаны концентрации компонентов реакции при равновесии в системе. Если реакция протекает в растворе, тогда концентрация компонентов реакции — моляльная концентрация, причем концентрация воды в разбавленном растворе равна единице. Если среди компонентов реакции есть твердая фаза, тогда концентрация данного компонента реакции так же равна единице. Если среди компонентов реакции есть газовая фаза, тогда вместо концентрации газа в константе равновесия надо записать парциальное давление газа при равновесии. Например, константа равновесия реакции 3MgCO3 + 4SiO2 + H2O ⇔ Mg3Si4O10(OH)2 + 3CO2 при (Т > 373 °K),

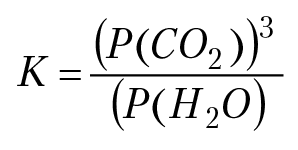
если Р — давление газовой фазы в системе, тогда Р(СО2) = χС × Р, Р(Н2О) = χН × Р (χi — мольная доля компонента газовой фазы в системе);

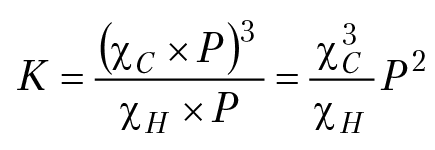
Получим уравнение Вант-Гоффа, с помощью которого можно вычислить значение константы равновесия химической реакции. Это уравнение называют так же изотермой химической реакции.

5.2. Константа равновесия химической реакции. Изотерма Вант-Гоффа

Пусть в термодинамической системе протекает химическая реакция:

aA + bB = dD

Изобарный потенциал реакции ∆G = ∑niµi и в нашем случае мы получим:

∆G = dµD – ( aµA + bµB ) = d(µ0D + RTln[D] ) – {aµ0A + RTln[A] +

+ bµ0B + RTln[B]} = dµ0D – aµ0A – bµ0B + RTln([D]d/[A]a × [B]b)

В полученном выражении для изобарного потенциала реакции, алгебраическая сумма dµ0D — aµ0A — bµ0B есть стандартный изобарный потенциал реакции, ∆G0298, ∆G0298 = dµ0D – aµ0A – bµ0B . Выполнив необходимые подстановки и преобразования, мы получим уравнение Вант-Гоффа, которое связывает концентрации компонентов реакции и изобарный потенциал:

(5.1)

При равновесии, ∆G = 0, а выражение [D*]d/{[A*]a × [B*]b} есть константа равновесия реакции aA + bB = dD,

RTnK= –∆G0298 (5.2)

В уравнении (5.2) выражения [D*], [A*], [B*] обозначают концентрации компонентов реакции при равновесии. Если выражение для стандартного изобарного потенциала подставить в уравнение Вант-Гоффа (5.1), мы получим изотерму реакции:

(5.3)

В уравнении (5.3) концентрации компонентов реакции не равны равновесным концентрациям. Полученное уравнение связывает изобарный потенциал реакции, константу равновесия и текущие концентрации компонентов реакции. В электрохимии изотерма реакции позволяет рассчитать ОВ потенциал раствора.

5.3. Оценка температурного интервала устойчивости минералов

Полученные в предыдущем разделе соотношения позволяют решить ряд интересных для геолога задач без громоздких расчетов.

Задача 5.1. Оценить температурный интервал устойчивости кальцита на поверхности Земли.

Решение: нам необходимо оценить температуру, начиная с которой минерал самопроизвольно будет распадаться на более простые компоненты при нагревании. С термодинамической точки зрения, нам надо оценить, при каких значениях параметров среды изобарный потенциал соответствующей реакции будет отрицательный. В качестве примера, вычислим температуру начала разложения кальцита на поверхности Земли: СаСО3 = СаО + СО2. Пусть разложение кальцита имеет место при Т = Т*. Тогда, при Т = Т*, изобарный потенциал реакции ∆G°(T∗) ≤ 0. Если предположить, что теплоемкость продуктов реакции равняется теплоемкости исходных компонентов реакции, ∆Ср = 0, то ∆G°(T*) = ∆G°298 – T*×∆S°298 и ∆G°(T*) < 0, если ∆G°298 — Т*∆S°298 < 0. T ≥ 298 + ∆G°298/∆S°298. Так как ∆G°298 = 131 559 (Дж/моль), ∆S°298 = 162 (Дж/мольК), Т ≥ 1110 °K. Таким образом, кальцит будет устойчив на поверхности Земли при нагревании до 837 °С.

5.4. Поля устойчивости минералов. Строение Земли

Мы разобрали решение задачи о термической устойчивости минерала на поверхности Земли. Не менее важно уметь рассчитывать устойчивость минералов в недрах Земли на значительной глубине. Для решения этой задачи имеет смысл кратко познакомиться с основными данными о строении Земли (рис. 5.1).

Рис. 5.1. Строение Земли

Краткие сведения о строении Земли. Земля — третья планета, считая от Солнца, представляет собой по форме геоид — несколько сплюснутый со стороны полюсов шар с радиусом 6400 км; средняя плотность Земли — 5,5 г/см3. На основании сейсмических методов изучения Земли было установлено оболочечное строение Земли: земная кора (мощностью от 5 до 60 км), мантия (до 2900 км) и ядро радиусом 3500 км. Различают земную кору континентального типа и океанического. Мощность земной коры континентального типа достигает 60 км и увеличивается в районах крупных горных массивов (например, Гималаи). Толщина коры океанического типа не превышает 5 км, а местами мантия соприкасается с океанической водой. Неоднородным является и температурный градиент. Так, например, в центральных частях Украинского щита температура возрастает на 60° на метр (60 м/град), в Домбасе — 30 м/град, на Кавказе — 10 м/град. Приблизительно оценить рост температуры и давления с глубиной можно по табл. 5.1.

Поля устойчивости минералов. В задаче 5.1 мы оценили температурный интервал устойчивости кальцита для фиксированного внешнего давления 1 бар, в котором парциальное давление углекислого газа 3 × 10–4 бар. В общем случае температура и давление в системе могут изменяться в широком диапазоне значений и соответственно параметры устойчивого состояния минерала будут зависеть от совокупного значения температуры и давления.

Таблица 5.1. Температура и давление в недрах Земли

Глубина (км)	10	20	60	140	200
Давление (Кбар)	3	5	15	45	80
Температура (°C)	180	270	620	1680	1950

Набор значений температуры и давления, при которых минерал будет устойчив (относительно процесса разложения на более простые компоненты), составляет двумерное числовое поле, которое называется поле устойчивости минерала. Рассчитать поле устойчивости минерала, значить вычислить значения температуры и давления в системе, при которых реакция разложения минерала не может протекать самопроизвольно.

В основу алгоритма расчета полей устойчивости минералов можно положить зависимость константы равновесия реакции от температуры и давления: RTlnK = –∆G(P, T). Вычисляя значения температуры и давления, при которых выполняется равенство, мы вычислим параметры равновесного состояния системы. Результаты­ расчета наносятся на диаграмму в координатах [P, T]. Затем необходимо разметить диаграмму: определить, при каких значениях температуры и давления в системе соответствующая реакция будет протекать в прямом или обратном направлении. На рисунке 5.2 представлена соответствующая диаграмма: поле устойчивости кальцита.

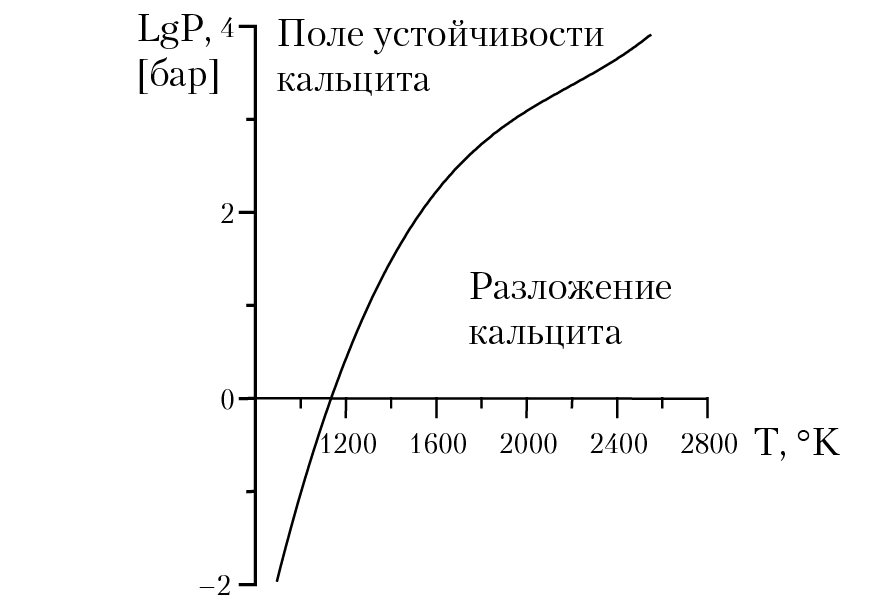
Рис. 5.2. Поле устойчивости кальцита

5.5. Поля устойчивости минералов в присутствии углекислотного и флюида

Если в состав минералов входят карбонильная [CO32–] и гидроксильные [OH–] группы, тогда параметры равновесного состояния такой системы при высокой температуре и давлении будут зависеть от параметров водно-углекислотного флюида (двухкомпонентной газовой фазы, в состав которой входя пары воды и углекислый газ). Расчет полей устойчивости минерала в этом случае несколько осложняется. Рассмотрим решение задачи на примере расчета полей устойчивости азурита. Поля устойчивости азурита Cu3(CO3)2(OH)2 надо строить в координатах [давление флюида]/[температура в системе], так как константа равновесия реакции термической диссоциации азурита зависит от параметров газовой фазы (флюида): Cu3(CO3)2(OH)2 = 3∗CuO + 2∗CO2 + H2O; К = (РСО2)2 × (РН2О). Если Р[бар] — давление газовой фазы (флюида), ξ — мольная доля паров воды во флюиде, тогда (1 — ξ) — мольная доля углекислого газа в флюиде; ξ Р — давление паров воды в системе, (1 – ξ)∗Р — давление углекислого газа в системе. Константа равновесия реакции диссоциации азурита: К = ξ Р[(1 – ξ) × Р]2 = ξ (1 – ξ)2 × P3.

Равновесие в системе по прежнему определяется уравнением:

∆G°(T) + 0,1 × ∆V × (P – 1) + RT × lnК = 0

∆G°(T) + 0,1 × ∆V × (P – 1) + RT × ln[ξ (1 − ξ)2×Р3] = 0

∆G°(T)[Дж/моль] — изобарный потенциал реакции при давлении 1 бар в системе; ∆V[см3/моль] — изменение мольного объема твердой фазы системы. В нашей задаче ∆V = 3∗Vтенорит – Vазурит. Vi (см3/моль) — мольный объем минерала. Мы по прежнему считаем, что твердые фазы системы несжимаемые, а газы подчиняются законам идеальных газов: PV = RT; литостатическое давление равно давлению флюида в системе. Данные ограничения не имеют принципиального значения. Зависимость мольного объема минерала от давления определяется коэффициентом изотермической сжимаемости

Значение β для минералов изменяется в пределах от 5 × 10–7 до 3 × 10–6 бар–1. Выполнив необходимое интегрирование, мы получим зависимость мольного объема минерала от давления. Не идеальность газов может быть учтена введением фугитивности газа fi = γi × pi. Коэффициент фугитивности γi, вычисляемый с помощью параметрических уравнений состояния газа, см. раздел 4.6 . Все это значительно усложняет конкретный расчет, но при использовании ЭВМ эти трудности разрешимы. На рис. 5.3 представлено поле устойчивости азурита для двух разных параметров флюида: кривая (1) соответствует флюиду, в котором мольная доля воды ξ = 0,4; кривая (2) соответствует флюиду, в котором мольная доля воды ξ = 0,1. Хорошо видно, что увеличение мольной доли воды во флюиде уменьшает поле устойчивости азурита. В случае, если пары воды и углекислый газ входят в состав флюида равными долями (в случае азурита, углекислого газа в составе флюида в два раза больше паров воды), тогда кривая (1) и (2) совпадают. Такая ситуация имеет место при расчете поля устойчивости малахита: Cu2(CO3)(OH)2 = 2CuO + CO2 + H2O.

5.6. Термодинамическое описание геотермометров и геобарометров

В основе построения геотермометров и геобарометров лежит термодинамический анализ обменных реакций между различными минералами. Равновесному состоянию системы будет соответствовать точно определенный состав твердого раствора при заданных значениях температуры и давления в системе. При изменении параметров состояния системы изменяется и состав твердого раствора до тех пор, пока не установится новое состояние равновесия. При равновесии твердых фаз, это наиболее четко можно проследить в перераспределении различных элементов между фазами. Рассмотрим один из алгоритмов перераспределения магния и железа между сосуществующими в равновесии твердыми растворами — биотитом и гранатом. Считаем, что биотит можно представить идеальным твердым раствором, в котором конечными членами являются флогопит KMg3[AlSi3O10](OH)2 и аннит KFe3[AlSi3O10](OH)2. Тогда для химической формулы биотита получим: KMg3XFe3(1–X)[AlSi3O10](OH)2, х — мольная доля магния в биотите.

Гранат представим твердым раствором, в котором конечными членами являются пироп Mg3Al2[SiO4]3 и альмандин Fe3Al2[SiO4]3. Тогда для химической формулы граната получим: Mg3YFe3(1–Y) [Al2(SiO4)3]. Y — мольная доля магния в гранате. При фиксированном значении температуры и давления установится точно определенное распределение магния и железа между биотитом и гранатом. При изменении температуры в системе это распределение магния и железа нарушится и при новом значении температуры установится новое распределение магния и железа между двумя твердыми растворами. Этот экспериментальный факт и положен в основу геотермометра. Достаточно измерить распределение магния или железа между биотитом и гранатом, чтобы определить температуру образования системы «биотит — гранат».

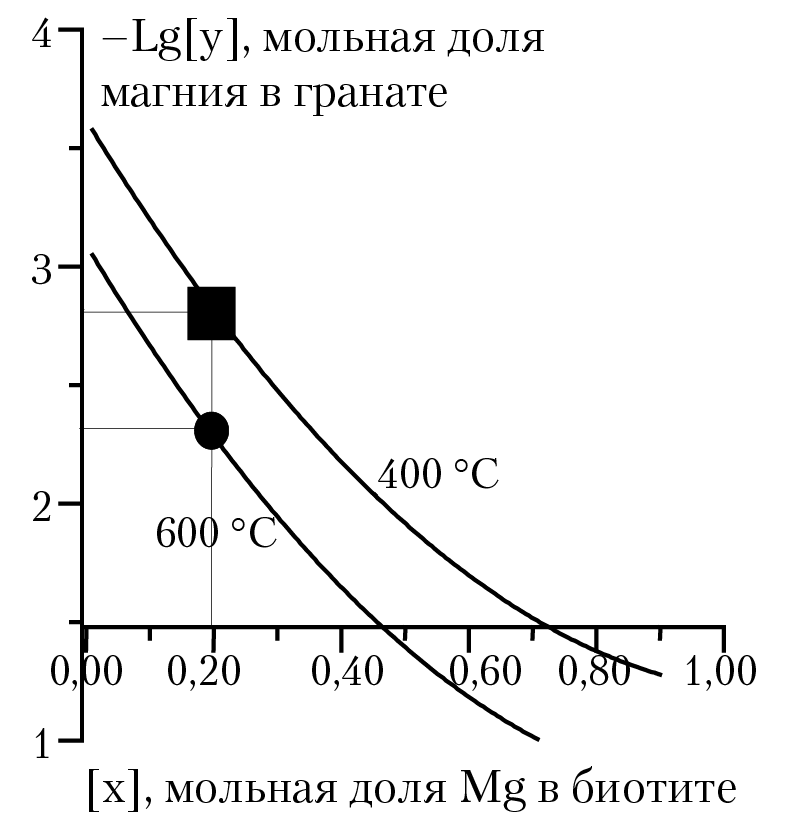
Рис. 5.4. Распределение магния между биотитом
и гранатом при давлении 2000 бар

Рассчитаем закон распределения магния или железа между сосуществующими твердыми фазами в зависимости от температуры образования твердых растворов. Равновесному состоянию биотита и граната соответствует равновесие обменной реакции между крайними членами изоморфных рядов:

KMg3X[AlSi3O10](OH)2 + Fe3(1–Y)Al2[SiO4]3 =

= Fe3(1–X)[AlSi3O10] (OH)2 + Mg3YAl2[SiO4]3

Так как в результате реакции происходит перераспределение магния и железа между твердыми фазами, для этого процесса константа равновесия равна:

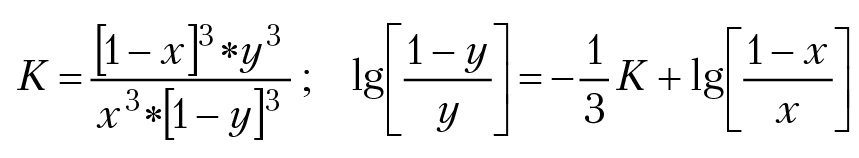
Полученное уравнение представляет собой зависимость мольной доли магния в гранате от мольной доли магния в биотите при равновесии. По уравнению Вант-Гоффа вычислим константу равновесия реакции:

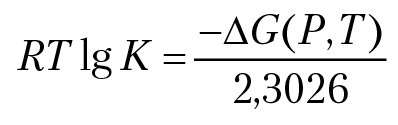
Изобарный потенциал реакции вычисляем по уравнению (10.1). Результаты расчетов зависимости y = f(x) для давления 2000 бар и температуре 400° и 600 °С представлены в виде графика на рисунке 5.4. Например, если мольная доля магния в биотите будет равна 0,2, то при 600 °С мольная доля магния в гранате будет равна 5,01 × 10–3, при температуре 400 °С мольная доля магния в гранате равна 1,58 × 10–3. Расчет равновесия в системе «биотит — гранат» выявил значительное влияние температуры на перераспределение­ магния и железа между двумя твердыми растворами, что позволяет рассматривать данную систему как геотермометр. Малое изменение мольного объема реакции (∆V = 0,04 см3/моль) указывает на то, что система «биотит — гранат» мало пригодна для построения геобарометра. В качестве потенциального геобарометра можно использовать перераспределения магния в зависимости от давления в системе «кордиерит + гранат». В этой системе изменение мольного объема реакции почти в 100 раз превышает соответствующее изменение в системе «биотит — гранат».