Физическая химия

4.1. Определение и физический смысл термодинамических потенциалов.
Понятие об изобарном потенциале реакции

4.2. Зависимость термодинамических потенциалов от параметров в закрытой системе

4.3. Зависимость изобарного потенциала от параметров в открытых системах.
Понятие о химическом потенциале

4.4. Зависимость химического потенциала от температуры

4.5. Зависимость химического потенциала от давления

4.6. Уравнения состояния газа

4.7. Зависимость химического потенциала от количества вещества

4.1. Определение и физический смысл термодинамических потенциалов.
Понятие об изобарном потенциале реакции

Р. Клаузиус сформулировал критерий направленности процессов в изолированной системе. Утверждается, что в изолированной системе возможны только такие процессы, в результате которых энтропия системы возрастает. ∆S > 0 — критерий направленности процессов в изолированной системе. Чрезвычайно полезно было бы иметь аналогичный критерий для предсказания направления процессов в любой термодинамической системе. Эта задача была решена в работах Вант-Гоффа, Гельмгольца, Гиббса и др. ученых. Если в системе протекает самопроизвольный процесс, то в общем случае система совершает работу, необходимую для перехода системы из одного состояния в другое. В чисто механических системах работа А, совершаемая во время превращения, равна изменению энергии системы, взятому со знаком минус: A = –∆E. Для процесса в термодинамической системе взамен равенства A = –∆U необходимо записать первый закон термодинамики: A = –∆U + δQ, т. е. работа, выполненная системой, может быть и больше запаса внутренней энергии системы, если будет обеспечен подвод тепла к системе. Отметим, что для циклического процесса (например, для идеальной тепловой машины), ∆U = 0 и A = δQ, т. е. система выполняет работу только за счет внешнего подвода тепла. Для дальнейшего расчета работы, выполняемой системой, удачной оказалась идея разбить работу на два слагаемых (Вант-Гофф, 1883): A = p∗∆V + δW. Первое­ слагаемое очевидно — это работа против внешнего давления. Второе слагаемое — это все остальные виды работы, которые способна совершить система. Это, например, работа по перемещению компонентов системы в пределах объема, занимаемого системой (Гугенгейм, 1941), работа, связанная с перемещением атомов или молекул в ходе протекания реакции, работа против электростатических сил при окислительно-восстановительных реакциях и т. д. Для равновесно протекающих процессов A = p∆V + δW, δQ = T∆S. Сделаем соответствующие подстановки в первом законе термодинамики: δQ = ∆U + A; A = δQ — ∆U. p∆V + δW = –∆U + T∆S. Вычислим δW. δW = T∆S — ∆ (U + pV). Для изобарного процесса ∆[U + pV] = ∆H(энтальпия процесса). Следовательно, δW = –(∆H – T∆S).

По определению, термодинамическую функцию ∆H – T∆S называют потенциал Гиббса и обозначают ∆G.

∆G = ∆H – T∆S (4.1)

Отметим, что потенциал Гиббса — функция переменных Р и Т, ΔG = f(P, T), и является функцией состояния системы; в закрытых системах дифференциал изобарного потенциала равен d(ΔG) = –ΔSdT + ΔVdP.

Так как работа, которую выполняет система при самопроизвольно протекающем процессе, равна δW = –(∆H – T∆S) = –∆G, то мы имеем право утверждать: если в системе протекает самопроизвольный процесс (т. е. работу, необходимую для протекания процесса, совершает система, следовательно, δW>0), то –∆G > O, ∆G < O. Используя понятие об изобарном потенциале процесса, мы можем теперь сформулировать понятие о критерии направленности самопроизвольно протекающего процесса в системе: если в ходе процесса изобарный потенциал системы убывает, процесс будет протекать самопроизвольно. Данный критерий направленности процесса мы получили при условии, что давление и температура в системе постоянны. По этой причине ∆G называют изобарно-изотермическим потенциалом. Если процесс в системе сопровождается выполнением конкретной работы W, тогда потенциал Гиббса данного процесса может быть вычислен по уравнению ∆G = –W. Например, при образовании кристаллов из расплава, образование поверхности раздела сопровождается затратой энергии W = –σS, σ[Дж/моль×м2] — коэффициент поверхностного натяжения на границе раздела фаз, S (м2) — площадь поверхности раздела. Следовательно, изобарный потенциал образования поверхности раздела ∆Gs = σS. В результате протекания окислительно-восстановительной реакции совершается работа по перемещению электрического заряда от восстановителя к окислителю. В пересчете на один моль заряда F = NA × e; (F — постоянная Фарадея, NA — число Авагадро, е — заряд электрона) работа по перемещению заряда W = F∆φ, следовательно, изобарный потенциал окислительно-восстановительной реакции ∆G = –F∆φ. Если в системе постоянными являются объем и температура, то можно показать, что изменение энергии в системе связано с работой δW = –(∆U — T∆S). Потенциал ∆F = ∆U – T∆S называют потенциал Гельмгольца или изохорно-изотермический потенциал процесса. Самопроизвольно могут протекать только такие изохорно-изотер­мические процессы, для которых ∆F < O. Таким образом, физический смысл термодинамических потенциалов очевидный — это критерии направленности самопроизвольно протекающих процессов в системе. Изменения в системе происходят в  результате протекания процесса или совокупности процессов. Инициировать процессы в системе можно путем изменения пара­метров состояния системы, в частности, путем изменения температуры, давления и количества вещества в системе. Предсказать направление процессов в системе после воздействия на систему — одна из важнейших задач термодинамики. Для решения поставленной задачи достаточно воспользоваться понятием изобарного потенциала процесса, так как мы уже показали, что процессы в системе направлены в сторону уменьшения изобарного потенциала системы. Одним из важнейших процессов, протекающих в системе, является химическая реакция. Если в результате процесса изменяется химический состав системы, то говорят, что в системе протекают химические реакции. После того, как было сформулировано понятие о потенциалах, была решена одна из главных проблем химии — во­прос о направлении химической реакции. Для этого достаточно вычислить изменение потенциал системы, в которой протекает данная реакция. Если процессы в системе связаны только с протеканием данной реакции, тогда понятия изменение потенциала системы и изобарный потенциал реакции являются синонимами. В качестве примера решим задачу: можно ли в 1 кг воды растворить 1 моль поваренной соли, NaCl. 1 моль соли 58 г, так что ответ нам заранее известен. С точки зрения термодинамики задачу сформулируем следующим­ образом: будет ли процесс растворения 1 моля соли при стандартных условиях протекания реакции самопроизвольным? Для решения задачи надо выписать из справочника значения стандартного изобарного потенциала образования компонентов реакции: ΔG°f298 = ΔH°f298 – 298S°298 и вычислить стандартный изобарный потенциал реакции.

NaCl = Na+ Cl–;

ΔG°f298: – 384 750 – 262 395 – 131 348;

ΔG°298 = – 262 395 – 131 348 – (–384 750) = –8993 (Дж/моль).

Изобарный потенциал реакции отрицательный, следовательно, в 1 кг воды 58 г соли растворятся.

4.1.1. Термодинамические соотношения для изобарного потенциала

В равновесных процессах δq = dU + PdV и dS = δq/T; δq = TdS, следовательно, TdS = dU + PdV.

По определению G = H – TS = U + PV – TS.

dG = dU +PdV + VdP – TdS – SdT = dU + PdV + VdP – dU – PdV – SdT.

После приведения подобных получим выражение для полного дифференциала изобарного потенциала:

dG = VdP – SdT (4.2)

Из уравнения (4.2) следует, что

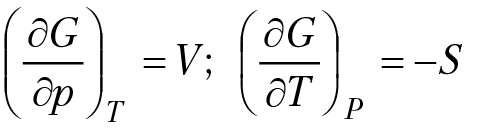(4.3)

Если ∆G — изменение изобарного потенциала, тогда

d∆G = ∆VdP – ∆SdT (4.4)

В общем случае изобарный потенциал является функцией не только давления и температуры в системе, но и количества веще­ства в системе, т. е. G = f(P, T, ni). С учетом возможного изменения количества вещества в системе, в уравнение 4.2 надо добавить соответствующее слагаемое:

(4.5)

С учетом 4.3 имеем:

dG = VdP – SdT + ∑µidni (4.6)

Коэффициент пропорциональности µi в уравнении 4.6 называется химический потенциал компонента системы, а уравнение 4.6 называется фундаментальное уравнение Гиббса.

4.1.2. Химический потенциал компонента газовой смеси

Вычислим изобарный потенциал одного моля идеального газа при постоянной температуре. Уравнение состояния идеального газа (уравнение Клапейрона–Менделеева) для 1 моля газа PV = RT. Если T = const, dG = VdP:

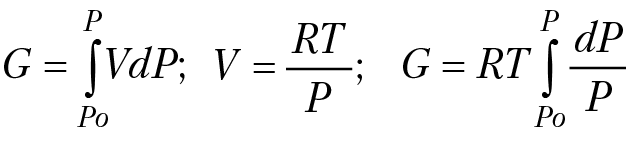
G = RTlnP – RTlnP0

cлагаемое RTlnP0 — это значение изобарного потенциала при опорном давлении Р0; если положить G° = – RTlnP0, тогда:

G = G° + RTlnP (4.7)

Если положить, что Р0 = 1 бар, тогда для компонента идеальной газовой смеси G° = 0. При изменении давления газа от Р1 до Р2, с учетом 4.6, ∆G = RT ln(P2/P1). Из уравнения 4.7 при изобарно-изотермическом процессе при условии, что в системе изменяется только количество только i-компонента, для химического потенциала получим:

из полученного выражения следует, что химический потенциал является парциальной мольной характеристикой компонента системы. С учетом уравнения 4.6 для i-компонента газовой смеси получаем:

µi = µ0i + RTlnPi (4.8)

Для идеального газа µ0 = 0, для реального газа Pi = fi/χi; fi, χi — фугитивность и коэффициент фугитивности газа (см. пункт 4.6) и µ0i ≠ 0.

Так как процессы в природе протекают в достаточно широком диапазоне изменения параметров системы, необходимо уметь рассчитывать зависимость термодинамических потенциалов от параметров системы.

4.2. Зависимость термодинамических потенциалов от параметров в закрытой системе

4.2.1. Зависимость изобарного потенциала от температуры

По определению ∆G = ∆H – T∆S, поэтому зависимость потенциала Гиббса от температуры определяется зависимостью от температуры энтальпии и энтропии реакции: ∆G(T) = ∆H(Т) – T∆S(Т). Используя уравнения Кирхгофа (3.3), получим:

∆G(Т) = ∆H°298 + ∫∆СрdT – T [∆S°298 + ∫(∆Ср /Т)dT]

Так как ∆G°298 = ∆H°298 – 298×∆S°298, после несложных преобразований, получим:

∆G(Т) = ∆G°298 + (298о – T)∆S°298 + ∫∆Ср(1 – 1/Т) dT

Если парциальные мольные теплоемкости компонентов реакции зависят от температуры в форме степенного ряда, Cp = a + b/T – c/T2, тогда (∆Cp) = ∆a + ∆bT – ∆c/T2; после подстановки в уравнение для ∆G°т, получим для зависимость изобарного потенциала реакции от температуры, соотношение:

∆G°т = ∆G°298 –∆S°298(T – 298,15) – ∆aTln(T/298,15) + ∆a(T –

298,15) – 0,5 ∆b(T – 298,15)2 + 0,5∆c(1/T)(T/298,15 — 1)2 (4.9)

4.2.2. Зависимость изобарного потенциала от давления в системе

Для расчета зависимости изобарного потенциала от давления, при постоянном количестве вещества в системе, воспользуемся тем фактом, что потенциал является функцией состояния системы, а значит дифференциал описывает полное изменение функции при изменении аргументов. Если в ходе процесса масса системы не изменяется, тогда d(∆G) = ∆VdP – ∆SdT и при T = const d(∆G)T = ∆V × dP; интегрируя последнее уравнение, получим:

∆G(Р)T = 0,1∆V(P – 1) + RTlnK (4.10)

где ∆V(моль/см3) — изменение мольного объема системы, P(бар) — литостатическое давление (давление на твердые фазы системы), K — константа равновесия процесса, в результате которого изменяется давление в системе. При вычислении интеграла

мы полагаем, что мольные объемы твердых фаз системы не зависят от давления, а газовая фаза — смесь идеальных газов.

Вычисление мольного объема реакции (∆V) и константы равновесия реакции (К). Пусть в системе протекает реакция термиче­ского разложения кальцита. Выписываем из справочника мольные объемы твердофазных компонентов реакции и вычисляем ΔV:

1 × СаСО3 = 1 × СаО + 1 × СО2

V(моль/см3): 36,94 16,76 газовая фаза;

∆V = 1 × 16,76 – 1 × 36,94 = –20,18 (см3/моль). Константа равновесия реакции К = Р(СО2) (Р(СО2) — давление углекислого газа при равновесии. Так как изобарный потенциал — функция состояния системы, при одновременном изменении давления и температуры, изменение изобарного потенциала системы можно записать как сумму: ∆G(P,T) = ∆G(T)p + ∆G(P)T.

4.3. Зависимость изобарного потенциала от параметров в открытых системах.
Понятие о химическом потенциале

Свойства системы зависят как от количества вещества в системе, так и от химической природы веществ, входящих в состав системы. Эта зависимость описывается с помощью понятия о химическом потенциале компонента системы. По определению, химическим потенциалом компонента системы называется частная производная от изобарного потенциала системы по количеству данного вещества в системе:

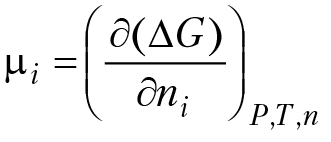
Из данного определения следует, что химический потенциал компонента определяет изменение изобарного потенциала системы при внесении dni(моль) данного вещества в систему (при фиксированных Р и Т): d[∆G] = µidni.

[µi] = Дж/моль. Полный дифференциал изобарного потенциа­ла образования системы или процесса в системе равен d(ΔG) = – ΔSdT + ΔVdP + ∑µidni. Последнее соотношение называется фундаментальное уравнение Гиббса.

Если мы создаем систему из ni-компонентов с химическими потенциалами µi, тогда изобарный потенциал образования системы будет равен: ∆G = Σ niµi.

Если в системе протекает реакция:

a1A1 + a2A2 + ... + aiAi = b1B1 + b2B2 + ... + bjBj

то изобарный потенциал реакции при температуре Т °К и давлении Р(бар) равен: ∆G(P,T) =∑bj × µj(р,т)(Bj) — ∑ai × µi(p,т)(Ai). µк(р,т) — химический потенциал компонента реакции при давлении в системе Р(бар) и температуре Т °К. Таким образом, чтобы вычислить изобарный потенциал реакции в открытых системах, надо уметь вычислять значения химических потенциалов компонентов реакции при произвольных значениях температуры и давления в системе. Зависимость химического потенциала от параметров системы может быть получена из фундаментального уравнения Гиббса:

dµm = – SmdT + Vmdp, (4.11)

где Sm — мольная энтропия компонента, а Vm — его мольный объем.

4.4. Зависимость химического потенциала от температуры

Температурная зависимость химического потенциала может быть получена интегрированием (4.11) при постоянной давлении в системе:

(4.12)

Здесь µ0 — химический потенциал при стандартных параметрах системы. Как видно из (4.12), зависимость химического потенциала от температуры определяется зависимостью энтропии компонента реакции от температуры. Эта зависимость может быть найдена из уравнения Кирхгофа:

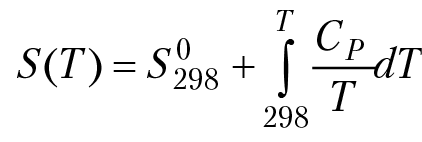
Cp — теплоемкость компонента реакции, S°298 — энтропия компонента реакции при стандартных параметрах. Выполняя интегрирование в (4.12) с учетом зависимости энтропии от температуры, получим:

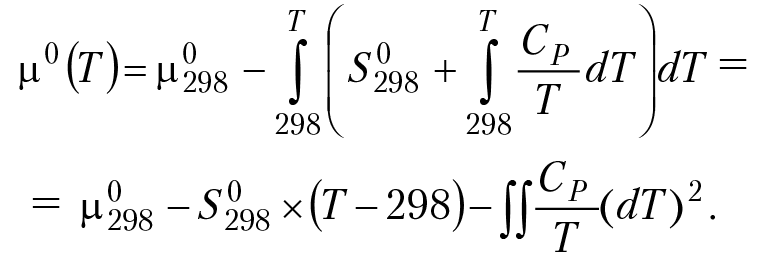
Считая, что теплоемкость компонента реакции зависит от температуры по степенному закону, CP = a + b×T – c/T2, получим зависимость химического потенциала компонента реакции от температуры:

µ(т)p= µ0298 — S0298 × (T–298) — a × lg(T/298) + a(T – 298) –

– 0,5b(T–298)2 + 0,5c × 1/T × (T/298 – 1)2 (4.13)

4.5. Зависимость химического потенциала от давления

При расчетах зависимости химического потенциала от давле­ния, необходимо рассмотреть различные приближения, которые при этом используются.

Барическая зависимость химического потенциала может быть получена интегрированием (4.11) при постоянной температуре:

(4.14)

Здесь Po — «опорное» давление, которое в большинстве случаев бывает удобно принять за стандартное Po = 1 бар, а µо — химический потенциал компонента при этом опорном давлении.

В общем случае в составе системы могут быть твердофазные компоненты, например, минералы и газовая фаза. Поэтому имеет смысл отдельно вычислить интеграл в (4.11) для твердофазного и газо-фазного компонента системы.

Зависимость химического потенциала от давления для твердофазного компонента системы. В этом случае необходимо знать зависимость мольного объема вещества от давления. Для минералов, не совершая большой ошибки, можно принять Vm = const, считая их несжимаемыми

В этом случае в результате интегрирования (4.14) получается простое выражение для зависимости химического потенциала минерала от давления P:

µ(p) = µo + Vm(P – P0) × 0,1 (4.15)

В этом уравнении P — давление в барах, Vm — мольный объем в см3/моль, µ — химический потенциал в (Дж/моль), а коэффициент 0,1 обеспечивает переход к системным единицам. При сверхвысоких давлениях наше предположение о не сжимаемости может оказаться неверным. Попробуем учесть это обстоятельство, введя изотермический коэффициент сжимаемости минерала (табл. 4.1).

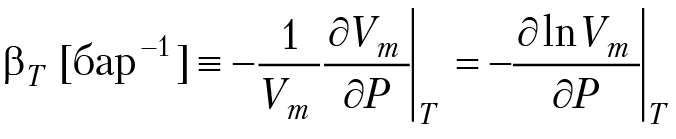
Интегрируя , получим lnVm/Vоm = – βT(P – Po), что эквивалент­но соотношению:

Vm = Vоm exp[– βT(P – Po)] (4.16)

где Vоm — мольный объем минерала при «опорном» давлении Po. Последнее уравнение можно рассматривать, как уравнение состояния минерала при постоянной температуре. Подставляя теперь (4.16) в (4.15) и интегрируя, получаем:

(4.17)

Поскольку –β(P – Po) мало, выражение (14) можно упростить, используя разложение e–x ≈ 1– x. Тогда

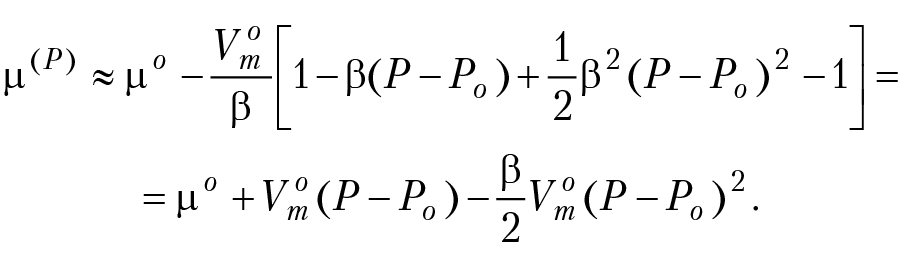
Окончательно получим с учетом переводного коэффициента 0,1

(4.18)

Легко видеть, что уравнение (4.18) переходит в (4.15), когда сжимаемостью можно пренебречь (β = 0). Всегда ли следует пользоваться громоздкой (хотя и более точной) формулой (4.18)? Для ответа на этот вопрос оценим, при каких давлениях второй член в квадратных скобках начинает играть существенную роль. Примем, что это происходит, когда Vom (P – Po) ~ β/2 Vom (P – Po)2. Принимая некоторое усредненное значение β = 2 × 10–6 бар–1, получим P ~ 106 бар, что соответствует давлениям, развиваемым в областях близких к ядру Земли. Для глубин, не превышающих 100 км, литостатическое давления не превысят 60 кбар. Это означает, что при проведении термодинамических расчетов более простое уравнение (12) работает достаточно успешно, а ошибка при этом не превысит 6 %. При анализе природных процессов с участием газовой фазы необходимо знать физико-химические свойства компонентов газовой фазы.

Таблица 4.1. Экспериментальные значения коэффициентов изотермической сжимаемости β
некоторых минералов при стандартной температуре 25 °С

Минерал	Альбит NaAlSi3O8	Альмандин Fe3Al2(SiO4)3
β⋅107 бар-1	20,2	5,6
Минерал	Анальцим NaAlSi2O6⋅H2O	Микроклин KalSi3O8
β⋅107 бар-1	19,7÷36,7	19,2
Минерал	Форстерит Mg2SiO4	Энстатит Mg2Si2O6
β⋅107 бар-1	7,9÷8,2	10,1
Минерал	Мусковит KAl3Si3O10(OH)2	Фаялит FeSiO4
β⋅107 бар-1	12	9,1

Наиболее часто геологу приходится сталкиваться с парами воды, углекислым газом СО2, азотом, кислородом и т. д. Химиче­ские свойства газов мы разберем в разделах лекций, посвященных взаимодействию газов с твердыми и жидкими фазами. Сейчас нас будет интересовать физико-химические свойства и поведение газовых растворов и компонентов этих растворов в широком диапазоне изменения температуры и давления. Соотношения, определяющие связь между параметрами газа, называются уравнениями состоя­ния газа. Получить эти уравнения является одной из основных задач термодинамики. Наиболее успешно эта задача решена для идеального газа.

4.6. Уравнения состояния газа

Идеальный газ. Уравнение Клапейрона—Менделеева. Идеаль­ный газ можно определить как термодинамическую систему, в которой взаимодействие между компонентами считается равным нулю, каждую молекулу такого газа рассматривают как упругий, недеформируемый шарик, размеры которого несоизмеримо малы, по сравнению с объемом, занимаемого газом. В этом случае несложно показать, что давление газа полностью определяется средней кинетической энергией молекул газа и равно: P = 2/3 × n(Eк), (EK) = 3/2 × kT, k = 1,38 × 10–23 (Дж/град), постоянная Больцмана, n = число молекул в единице объема. Если ν — число молей газа в объеме V, то n = (ν × NA)/V, NA = 6,022 × 1023 (1/моль). Так как R = k × NA = 8,31441 Дж/(мольК), (газовая постоянная), после несложных преобразований получим уравнение состояния идеального газа:

P. V = νRT

Если Р — давление газа в барах; Vm — молярный объем в см3/моль; Т — температура в °К; тогда R = 83,1441 (бар×см3/моль×К).

При невысоких значениях температуры и давления, такие газы, как пары воды, углекислый газ, азот, кислород подчиняются уравнению состояния идеального газа.

Уравнение Ван-дер-Ваальса. К сожалению следует отметить, что при повышении давления и температуры, модель идеального газа становится непригодной для анализа газовой фазы системы. Необходимо отказаться от представления о молекулах газа, как о лишенных размеров шариках, и от предположениях, что силы взаимодействия между молекулами отсутствуют. Уравнение состояния, в котором учтены как конечные размеры молекул, так и силы взаимодействия между ними, было в 1873 г. предложено голландским физиком Ян Дидерик Ван-дер-Ваальсом. При учете конечных размеров молекул, необходимо из объема сосуда вычесть ту ее часть, которая не доступна для движения молекул. Обозначим ее через параметр b. Если продолжать считать молекулы газа твердыми шариками, получим, что b = (16/3).πr3NA . Параметр молекулы r носит название газокинетический радиус молекулы. По порядку величины, b ≅ n. 10–5 (м3/моль). С учетом поправки b, уравнение (16) примет вид: P (V – b) = RT (в пересчете на один моль газа).

Поправка b связана с учетом сил взаимодействия между молекулами газа. Учет сил притяжения приводит к уменьшению давления газа на любую поверхность, т. е. P = RT/(V – b) – ∆P. Так как ∆P ≅ n2, a n обратно пропорционально объему, занимаемого газом, получим: ∆P = a/V2. Подставляя полученное выражение для ∆Р в предыдущее уравнение, получим уравнение Ван-дер-Ваальса для ν молей газа (4.19):

(4.19)

Например, для углекислого газа а = 3,65 [(бар.см3/моль2], b = 42,8. (см3/моль), R = 83,1441 (см3∙бар)/(моль∙К); для паров воды а = 5,524, b = 30,413. Уравнение (4.19) после несложных преобразований можно привести к виду (для ν = 1):

На рисунке 4.1 приведены изотермы Ван-дер-Ваальса. Участок ga соответствует жидкофазному состоянию системы, ch-газообразному состоянию, af и dc — метастабильным состояниям жидкости и газа соответственно, (переходные состояния перед конденсацией газа или испарением жидкости). На рисунке 4.1 приведены две изотермы, причем Т2 > Т1. По мере повышения температуры, изотермы располагаются выше и при определенной температуре максимумы и минимумы изотерм сливаются, вырождаясь в точку перегиба К. При этой температуре исчезает различие между разными состояния­ми вещества. Это есть критическая температура, существование которой является характерным свойством вещества. Нетрудно вычислить значение критической температуры и соответствующей ей давление и объем:

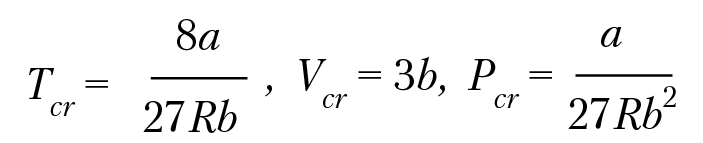(4.20)

Рис. 4.1. Изотермы Ван-дер-Ваальса

Для паров воды Тcr = 647,3К, Рcr = 221,2 бар, Vcr = 56,3 см3/моль. При этих значениях параметров газа левая часть уравнения Ван-дер-Ваальса должна быть точным кубом:

(4.21)

Это равенство выполняется, если Тср, Рср и Vср соответствуют равенствам (4.20).

Современные модификации уравнения Ван-дер-Ваальса. Большинство видоизменений уравнения Ван-дер-Ваальса учитывает зависимость параметров a и b от температуры и давления. В настоящее время известно более 150 видов уравнения состояния газа. Все они в той или иной форме являются вириальными уравнениями. Вид уравнения определяется вириальными коэффициентами, значения которых определяются или экспериментально, или из конкретной модели межмолекулярного взаимодействия. Коэффициенты потому и называются вириальными, что они определяются силой взаимодействия между молекулами газа. В общем виде вириальное уравнение состояния имеет вид:

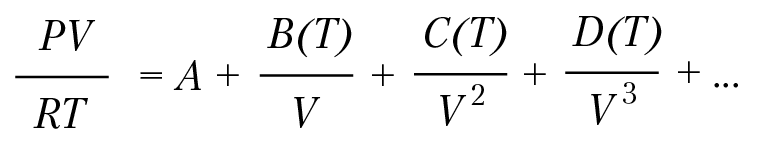
Очевидно, что вириальные коэффициенты должны обеспечить сходимость степенного ряда. В 1903 г. Д. Бертелло предложил уравнение состояния газа:

Уравнение Битти — Бриджмена:

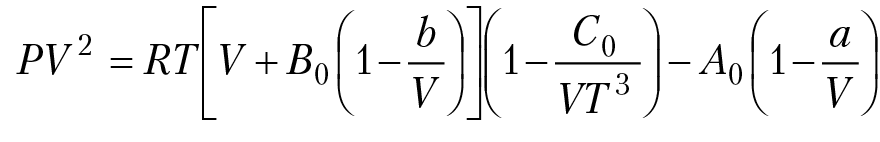
Уравнения состояния, которые наиболее часто используются при расчетах параметров состояния газа, по своей сути, параметрические уравнения. Значения параметров, как правило, получают из анализа экспериментальных данных. Таким уравнением является уравнение Редлиха—Квонга:

(4.22)

В уравнении (20), [Р] = бар, [V] = см3/моль, [R] = 83,1441 (см3 бар)/(мольК). Значения параметров [a, b] приведены в табл. 4.2.

Таблица 4.2. Значения параметров (a, b) в уравнении Редлиха—Квонга

	Н2	О2	СО2	СН4	Н2О
α × 10–6	1,81	17,37	64,70	32,00	88,00
b	15,34	22,08	29,70	29,70	14,60

Мы рассмотрели различные уравнения состояния газа. Выбор конкретного уравнения состояния газа зависит от термодинамической модели процесса, в котором присутствует газовая фаза. В случае, когда температура газа невысокая, а давление мало, можно считать, что его поведение описывается простым уравнением состояния идеального газа: PV = RT. Здесь P — давление газа в бар, V — его молярный объем в см3/моль, T — температура в абсолютной шкале, а R = 83,1441 — универсальная газовая постоянная, выраженная в бар×см3/(моль×K). Интегрирование фундаментального уравнения Гиббса (4.11) dµm = –SmdT + VmdP, при постоянной температуре позволяет получить бариче­скую зависимость химического потенциала идеального газа:

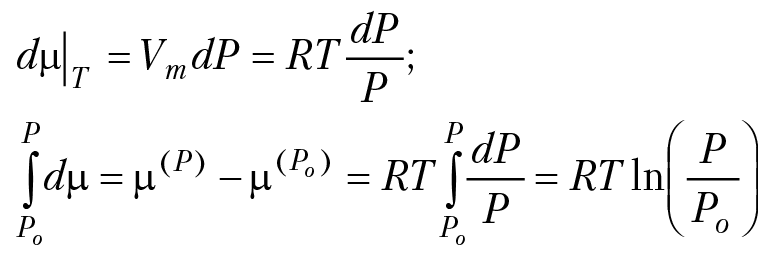
Принимая опорное давление Po равным стандартному Po = 1 бар, получим окончательно:

µ(p) = µo + RTln(P, бар) (4.23)

где µo — химический потенциал газа при стандартном давлении. Если имеется смесь газов, то P в уравнении (4.10) — это парциальное давление данного газа в смеси1. Чтобы не путать его с общим давлением в системе, условимся в дальнейшем обозначать парциальные давления газов строчной буквой p.

Если реальный газ описывать с помощью (4.10), то с увеличением давления и снижением температуры начинают накапливаться ошибки. В этом случае для описания реального газа в термодинамике вводится понятие летучести (или фугитивности) f:

µ(p) = µo + RT ln(f, бар) (4.24)

Летучесть несет в себе информацию о давлении газа и о степени отклонения этого газа от идеального. Обычно летучесть представляют в виде произведения:

f = γ p (4.25)

где γ — коэффициент летучести газа (безразмерная величина). Коэффициент летучести зависит от условий (давления и температу­ры), но достигает единицы при очень низких давлениях, когда поведение газа стремится к идеальному γ|p→0→1; f|p→0→p.

Если теперь проинтегрировать уравнение Гиббса с учетом уравнения состояния реального газа

 

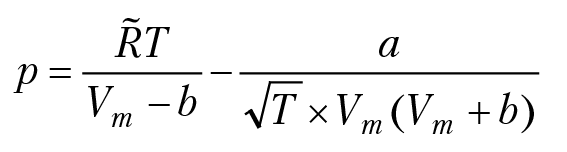
то можно получить выражение для коэффициента летучести:

(4.26)

В качестве иллюстрации на рис. 4.2 приведены температурная и барическая зависимости коэффициента летучести CO2, рассчитанные по уравнению (4.26).

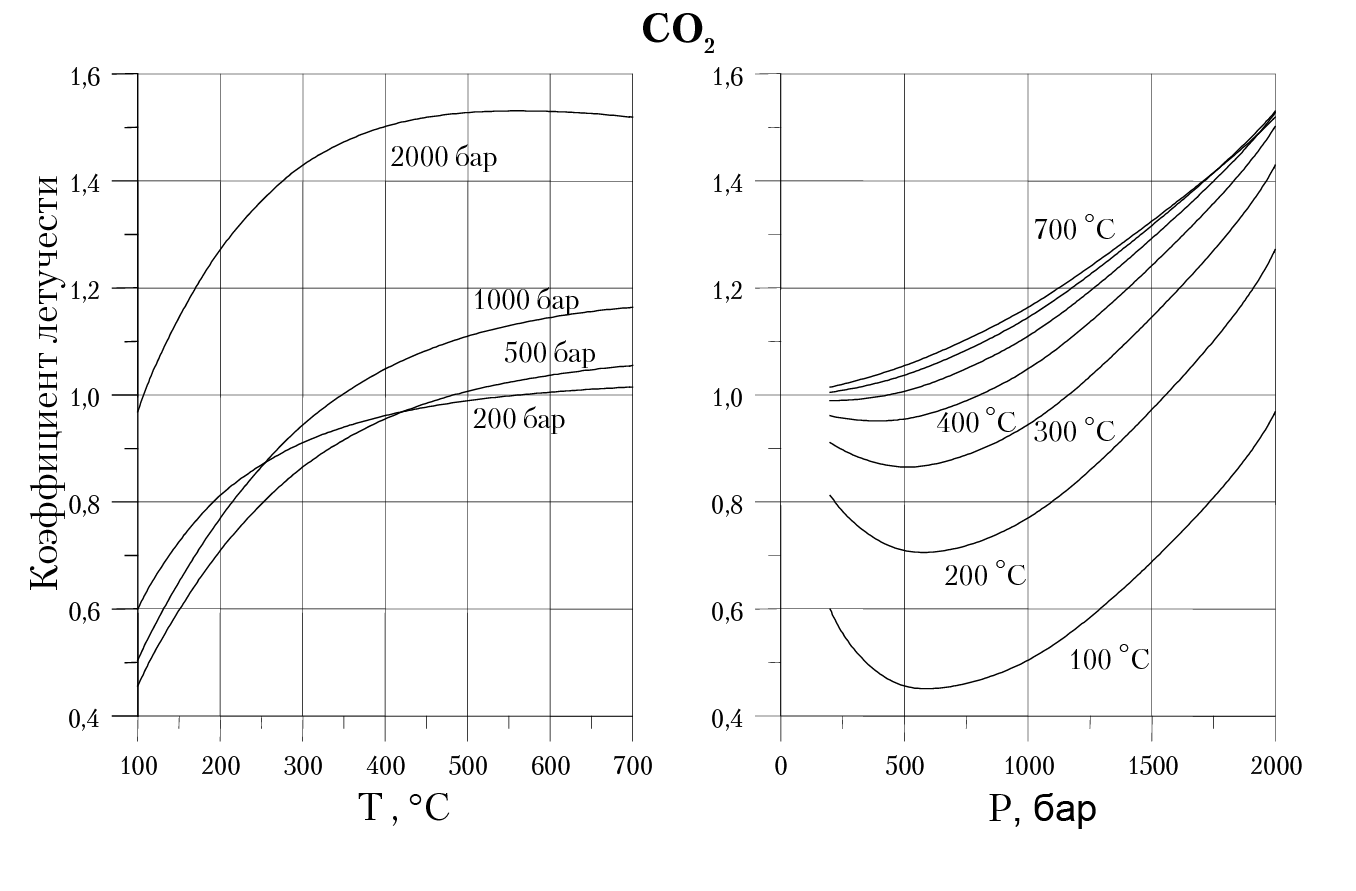
Рис. 4.2. Температурная и барическая зависимость
коэффициента летучести углекислого газа

Описание смеси газов опять начнем со случая идеальных компонентов. Тогда для описания газа i можно использовать уравнение

µ(p)i = µoi + RTln(pi) (4.27)

где µoi — стандартный химический потенциал чистого газа i , а pi — его парциальное давление в смеси. Парциальное давление связано с общим давлением в системе P простым уравнением Дальтона: pi = xiP, в котором xi — мольная доля газа i в смеси. Уравнение для химического потенциала тогда примет вид:

µ(p) i = µoi + RTln(xiP) (4.28)

Для смеси реальных газов следует записать:

µ(p) i = µoi + RTln(γi xiP) (4.29)

где γi — коэффициент летучести газа в смеси. Если взаимодей­ствие между разнородными молекулами не сильно отличаются от взаимодействия между одинаковыми, можно считать, что коэффициент летучести газа γi в смеси газов равен таковому для этого же чистого газа, но находящегося при общем давлении P: γoi (P, T). Здесь индекс «o» подчеркивает, что коэффициент летучести относится к чистому газу. Теперь (28) перепишется в виде µ(p)i = µoi + RTln(γixiP), а выражение для летучести газа при общем давлении P и температуре T примет вид:

Последнее соотношение в научной литературе называется правилом Льюиса — Рендалла и с хорошей точностью применимо для большого числа природных газовых смесей в широком диапазоне изменения температуры и давления. Какие из полученных формул использовать для расчета зависимости химического потенциала компонента реакции от параметров системы определяется физико-химической моделью исследуемого процесса и возможностями вычислительной техники. Всегда имеет смысл выполнить упрощенный расчет и только тогда уточнить полученный результат, используя более сложные алгоритмы.

4.7. Зависимость химического потенциала от количества вещества

Для компонента газовой фазы системы эта зависимость определяется уравнением µi = µ*i + RT lnpi, где µ*i — химический потенциал компонента при давлении 1 бар и температуре Т °К; если Т = 298 °К, то µ* = µ0 (табличное значение химического потенциала); pi(бар) — парциальное давление i-го компонента в системе. Для твердой фазы системы (химически чистого вещества) относительное количество данного вещества в фазе равно единице (вся фаза состоит из данного вещества) и, следовательно, химический потенциал твердой фазы не будет зависеть от количества вещества: µ = µ* + RTln1 = µ*.

Примечание: для стандартного значения химического потенциала твердой фазы при Т = 298 °К принято другое обозначение: µ° = G°f298. Это надо иметь ввиду при работе с термодинамическими таблицами. Для компонентов другой природы мы определим выражение для химического потенциала в соответствующих разделах лекций.

---