3.3. Работа термодинамической системы против внешних сил
3.4. Применение первого закона термодинамики к анализу тепловых процессов
3.5. Энтальпия химической реакции. Определение и физический смысл энтальпии. ∆H°f298 и ∆H°298
3.7. Предмет и основные понятия второго закона термодинамики
3.8. Энтропия. Определение и физический смысл понятия
3.9. Изменение энтропии как критерий направленности и равновесия в изолированной системе
3.11. Зависимость энтропии и энтальпии от температуры
3.12. Расчет изменения энтропии для некоторых термодинамических процессов
3.13. Тепловая теорема Нернста (третье начало термодинамики)
3.1. Предмет и задачи химической термодинамики.
Основные понятия и определения.
Классификация термодинамических систем и процессов
Термодинамика, как один из разделов физической химии, имеет огромное практическое значение, поскольку позволяет доводить умозрительные построения до расчетного, строго контролируемого решения. В настоящее время в геологических исследованиях наиболее широко используются методы и законы термодинамики равновесных процессов. Этим вопросам уделяется повышенное внимания в данном разделе лекций.
При анализе природных процессов методами термодинамики, нам придется пользоваться рядом понятий и определений, которые составляют язык термодинамики. Определим эти понятия.
Система — тело или совокупность тел, мысленно или фактически выделенных из окружающей среды и являющиеся предметом изучения. Например: минерал, рудное тело, раствор, ионосфера и т. д. В зависимости от характера взаимодействия системы с внешней средой определяют понятие изолированной системы, замкнутой системы и открытой системы. При анализе процессов, протекающих в изолированной системе, предполагается полное отсутствие обмена энергией и веществом системы с окружающей средой. Данная система является чисто теоретическим понятием и в природе не реализуется. Для замкнутой системы разрешается обмен энергией, но запрещается обмен веществом системы с внешней средой. Примером такой системы могут служить газожидкие включения в минералах. Для открытых систем имеет место обмен и энергией и веществом с внешней средой. Можно считать, что природные системы — это в основном открытые системы.
Параметры системы — совокупность физико-химических характеристик системы (температура, давление, объем, количество вещества, электрический потенциал и т. д.). Стандартные параметры системы: количество вещества — один моль, температура — 298,15 К, давление — 1 бар, количество воды в системе — 1 кг, концентрация компонента в растворе (моляльная концентрация) — 1 моль/1 кг воды.
Уравнение состояния системы — уравнение, которое связывает между собой параметры, которые характеризуют состояние системы. Например: система — идеальный газ; параметры состояния — температура Т °К, давление Р, объем V; уравнение состояния: (P × V) = (m/µ)RT.
Классификация термодинамических процессов. Термодинамический процесс — это всякое изменение состояния системы, сопровождающееся изменением хотя бы одного из параметров системы. Процесс называется самопроизвольным, если он протекает без внешнего воздействия на систему и поступления энергии. Равновесным называется процесс, проходящий через непрерывный ряд равновесных состояний. Под равновесным состоянием системы понимается такое состояние, которое принимает система после завершения всех процессов в системе и которое сохраняется во времени до начала следующего термодинамического процесса. Обратимый процесс — это процесс, который может быть проведен в обратном направлении без того, чтобы в системе и окружающей среде остались какие-либо изменения. Как правило, равновесные и обратимые процессы совпадают.
3.2. Первый закон термодинамики. Основные понятия закона и формулировка. Понятие о функции состояния системы
Среди процессов, протекающих в природе, огромное значение играют тепловые процессы. Поглощением или выделением тепла сопровождается рудообразование, карстовые процессы, растворение и кристаллизация веществ, сжигание топлива и радиоактивные процессы Поэтому правомерно поставить вопрос: что произойдет с термодинамической системой, если мы привнесем в систему энергию в форме тепла? Ответ на этот вопрос в общем виде дает первый закон термодинамики.
δq = ∆U + δA (3.1)
Если системе сообщить некоторое количество тепла, то изменится внутренняя энергия системы и система способна совершить работу против внешних сил.
Форма передачи энергии системе в процессах теплопереноса (когда мы нагреваем или охлаждаем систему) называется теплотой, а мера переданной энергии в таком процессе есть количество теплоты. Внутренняя энергия системы является частью полной энергии системы, так как энергия системы складывается из внутренней энергии системы, потенциальной и кинетической энергии системы как единого целого: E = U + (П+К). В понятие внутренней энергии системы включают поступательную и вращательную энергию молекул, колебательную энергию атомов в молекуле, энергию движения и взаимодействия электронов в атоме, внутриядерную энергию. Внутренняя энергия системы зависит от природы вещества, его количества в системе и от параметров состояния системы. Изменение внутренней энергии ∆U зависит только от значения параметров системы вначале и в конце процесса и не зависит от пути перехода системы из начального состояния в конечное состояние. Термодинамическая функция, обладающая таким свойством, называется функцией состояния системы. Внутренняя энергия системы — функция состояния системы. Условимся в дальнейшем относить внутреннюю энергию к одному молю вещества. В термодинамике энергия системы определяется при строго фиксированном значении потенциальной и кинетической энергии системы как целого, т. е. П+К = const, поэтому ∆E = ∆U + ∆(П+К)= ∆U. Таким образом, при анализе термодинамических процессов полное изменение энергии системы равно изменению ее внутренней энергии: ∆E = ∆U.
Вычислить внутреннею энергию можно только для идеального газа (без учета ядерной энергии). Согласно закону равнораспределения энергии классической статистической физики (Больцман) U = i/2 RT (для одного моля газа): i — число степеней свободы молекулы газа (числом степеней свободы частицы называется число независимых координат, которые определяют положение и конфигурацию частицы в пространстве).
1. Одноатомный идеальный газ: i = 3, U = 3/2 RT;
2. Двухатомный идеальный газ: i = 6, U = 6/2 RT = 3RT.
3.3. Работа термодинамической системы против внешних сил
В уравнение (3.1) входит понятие «работа термодинамической системы». В общем случае элементарное количество выполненной работы (т. е. бесконечно малый объем работы) можно записать в виде произведения обобщенной силы Fi на изменение обобщенной координаты ξi, т. е. δA = Fi × ξi. Например, работа, совершаемая против внешнего давления Р при изменении объема системы ΔV равна: δA = P∆V; работа против сил электрического поля равна q × ∆φ (∆φ — разность потенциалов электрического поля, q — величина перемещаемого заряда; данный вид работы играет важную роль при анализе окислительно-восстановительных реакций); работа, при изменении поверхности системы dS равна σdS; σ — поверхностное натяжение. Если в состав системы входит газовая фаза, при анализе работы, совершаемой такой системой, важную роль играет работа расширения газа:
в разных процессах.
1. В изохорном процессе, V = const, dV = 0, A = 0.
2. В изобарном процессе, P = const: A = P(V2 – V1).
3. В изотермическом процессе, T = const: для одного моля идеального газа PV = RT, P = RT/V и
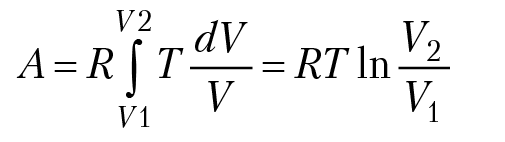
4. В адиабатическом процессе, δQ = 0: A = –∆U (работа совершается за счет уменьшения внутренней энергии системы).
3.4. Применение первого закона термодинамики к анализу тепловых процессов
Всякие химические превращения сопровождаются изменением внутренней энергии компонентов реакции, а значит и всей системы в целом. Согласно первому закону термодинамики, ∆U = δq + (–δA). В зависимости от условий протекания процесса в системе, изменение внутренней энергии системы ∆U может разным способом распределяться между двумя слагаемыми. Наибольшая теплота, которую можно получить для данного процесса, называется тепловым эффектом процесса. Примечание: в термохимии принято считать тепловые эффекты экзотермических реакций (теплота выделяется в ходе протекания реакции) положительными, а эндотермических реакций — отрицательными. В термодинамике принята противоположная система знаков: δq > O, если в результате процесса тепло поглощается и δq < O, если тепло выделяется. Для того чтобы согласовать обе системы знаков, будем обозначать тепловые эффекты процессов буквой Q и считать, что Q = –δq.
3.5. Энтальпия химической реакции. Определение и физический смысл энтальпии. ∆H°f298 и ∆H°298
Большое значение имеет теоретический расчет теплового эффекта химической реакции. Эту задачу можно решить на основании первого закона термодинамики. Действительно, за исключением специально организованных химических процессов, работа, которая связана с протеканием реакции в системе, есть работа против внешнего давления: δA = p × ∆v (∆v — изменение объема системы в результате протекания реакции). В этом случае первый закон термодинамики можно записать в виде уравнения: δq = ∆U + p∆v. Для изохорических процессов (v = const, ∆v = 0), δq = ∆U, а тепловой эффект реакции Qv = –∆U. Для изобарических процессов (p = const, p∆v = ∆ [pv]), δq = ∆U + ∆ [pv] = ∆ [U + pv] = ∆H. Термодинамическая функция H = U + pv называется энтальпия системы, а изменение энтальпии с обратным знаком (−∆H) равно тепловому эффекту изобарного процесса, Qp = −∆H. Необходимо отметить, что мы не располагаем способом для определения абсолютного значения внутренней энергии, а значит и энтальпии системы. К счастью, этого и не требуется, так как нам надо уметь вычислять разности: ∆U = Uк – Uн и ∆H = Hк — Hн. Uк — энергия конечного состояния системы, Uн — энергия начального состояния системы. Энтальпия термодинамической системы — функция состояния системы. При расчетах разностных значений функции состояния, выбор точки отсчета может быть сделан произвольным образом. В настоящее время принято считать, что энтальпия образования простых веществ в стандартных состояниях равна нулю. Например, стандартная энтальпия образования кислорода при температуре Т = 298 °К и давлении газа один бар, равна нулю: ∆H°f298(O2) = 0, стандартная энтальпия образования графита ∆H°f298(Сграфит) = 0. Но стандартная энтальпия образования алмаза уже не равна нулю: ∆H°f298(Салмаз) = 2900 (Дж/моль), т. е. графит считается простым веществом, а алмаз — сложным. Теперь мы можем определить стандартную энтальпию образования сложного вещества, ∆H°f298[Дж/моль] . Определение: стандартной энтальпией образования вещества называется энтальпия образования этого вещества из простых веществ в их стандартных состояниях. Например, энтальпия образования воды будет равна энтальпии реакции: Н2 + 0,5О2 = Н2О, если проводить эту реакцию при давлении компонентов один бар и температуре 298 °К. Тепловой эффект реакции образования одного моля газообразной воды равен Qp=241 840(Дж/моль), следовательно, ∆H°f298(H2O)пар = –241 840 (Дж/моль). Отметим, что стандартная энтальпия образования воды в жидкой фазе равна ∆H°f298(H2O)жидк = –237 150 (Дж/моль). Стандартную энтальпию образования вещества заносят в термодинамические справочники.
Расчеты тепловых эффектов химических реакций. В 1840 г. русский академик Г. И. Гесс опытным путем установил основной закон термохимии: тепловой эффект химических процессов в системе зависит только от начального и конечного состояния системы и не зависит от пути перехода системы из начального состояния в конечное состояние. Например, двуокись углерода можно получить сжиганием угля в кислороде непосредственно до двуокиси углерода, или получить сначала окись углерода, а затем дожечь ее до двуокиси углерода. Тепловой эффект первого пути получения СО2 : С + О2 = СО2 + 94,05 Ккал. Тепловой эффект получения СО2 в две стадии равен:
С + 0,5О2 = СО + 26,42 Ккал, СО + 0,5О2 = СО2 + 67,63 Ккал.
Всего: 94,05 Ккал.
Совершенно очевидно, что закон Гесса является следствием закона сохранения энергии. Действительно, если количество тепла, выделяющееся на различных путях проведения реакции, было бы неодинаковым, то можно было бы получить энергию из ничего, направляя реакцию в прямом направлении по одному пути, а в обратном направлении по другому пути. Отметим, что закон Гесса имеет большое значение для получения термохимических констант, в частности для определения стандартной энтальпии образования вещества. Закон Гесса, а так же тот факт, что энтальпия термодинамической системы является функцией состояния системы, позволяет проводить расчеты тепловых эффектов химических реакций по достаточно простому алгоритму: сначала вычисляем энтальпию химической реакции, а затем по уравнению Qp = –∆H вычисляем тепловой эффект реакции.
Задача 3.1: вычислить тепловой эффект реакции электролитической диссоциации одного моля соды.
Решение: выписываем из справочника стандартную энтальпию образования компонентов реакции:
Na2CO3 = 2Na+ CO32–
∆H°f298: –1131437 –240220 –676490
Энтальпия реакции при стандартных условиях равна:
∆H°298 = 2(–240 220) + (–676 490) – (–1 131 437) = –25 493 (Дж/моль).
Ответ: тепловой эффект реакции электролитической диссоциации Qp = +25493 Дж/моль.
3.6. Теплоемкость вещества и реакции. Зависимость теплого эффекта реакции от температуры. Уравнение Кирхгофа
Алгоритм расчета теплового эффекта реакции, при стандартных условиях протекания реакции, относительно прост. Возникают проблемы при расчетах теплового эффекта реакции при повышенных значениях температуры и давления в системе. Зависимость теплового эффекта реакции от температуры определяется зависимостью теплоемкости компонентов реакции от температуры. Определим основные понятия, связанные с расчетом теплового эффекта реакции от температуры. Молярной теплоемкостью вещества называется количество теплоты, которое необходимо сообщить одному молю вещества, чтобы нагреть его на один градус С = Q/∆T; [C] = Дж/(моль×К), ∆Т = 1°. Чтобы нагреть m молей вещества на ∆T градусов необходимо затратить количество тепла Q = m×С×∆T. В общем случае теплоемкость вещества зависит от температуры и давления. Для изохорной теплоемкости газа (V = const, dV = 0)
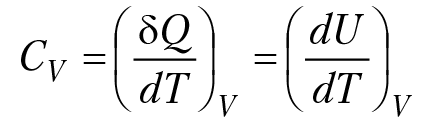
для идеального газа U = i/2RT, CV = i/2R. Для одноатомного газа i = 3, CV = 3/2R. Cp = CV + R = 5/2R. Для кристаллических веществ (в частности, для минералов) зависимость теплоемкости вещества от температуры представляют в виде степенного ряда: Ср = а + вТ – сТ–2. Коэффициенты а, в, с вычисляют на основании экспериментальных данных и заносят в справочники. Например, для кальцита, а = 04,42 [Дж/(моль×К)], в = 0,0219 [Дж/(моль×К2)], с = 2,6 × 106 [(Дж/К)/моль]. Рассчитать зависимость теплоемкости кристаллического вещества можно по уравнению Дебая:
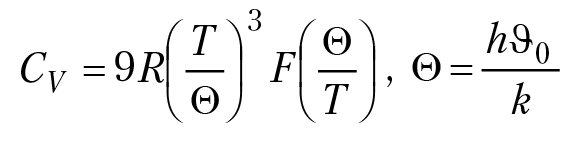
характеристическая температура данного кристаллического вещества, Θ = 4,94 ×10–11υ0; υ0 — максимальная частота колебания атомов в кристаллической решетке данного вещества; F(Θ/Т) — функция Дебая, для которой существуют табличные значения в зависимости от Θ/Т. Для расчета Θ с атомной кристаллической решеткой (например, для металлов) используют уравнение Линдемана:
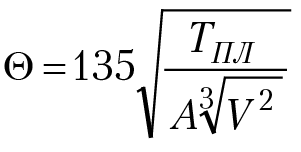
где Тпл, К — температура плавления вещества;
А — атомный вес вещества;
V[см3/моль] — атомный объем вещества.
Например, для свинца Тпл = 600 °К, А = 207, V = 18,3 см3/моль, Θ = 95 °К. Для расчета СР = СV(1 + 0,0214CV[T/Tпл]). Если в термодинамической системе протекает реакция, то зависимость изменения теплоемкости системы ∆Ср от температуры можно вычислить по уравнению ∆Ср = ∆а + ∆в × Т + ∆с × Т–2, где ∆ есть разность между соответствующими коэффициентами теплоемкости продуктов реакции и исходных веществ, записанная с учетом стехиометрических коэффициентов химического уравнения. При расчетах зависимости теплового эффекта реакции от температуры при стандартном давлении необходимо проинтегрировать уравнение
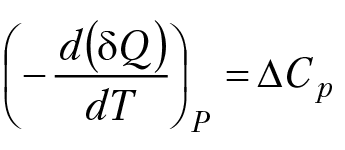
так как δQp = – ∆H°, получим: d(∆H°) = ∆CP×dT,
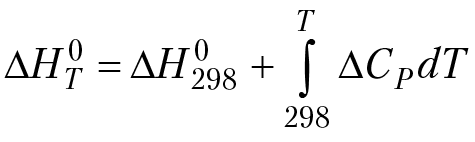
(уравнение Кирхгофа).
где ∆H°T — энтальпия реакции при температуре Т °К,
∆H°298 — энтальпия реакции при температуре 298 °К.
Выполняя интегрирование для степенной зависимости теплоемкости компонентов реакции от температуры, получим:
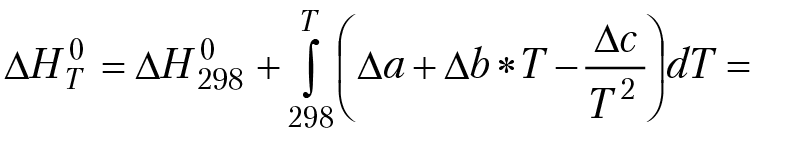
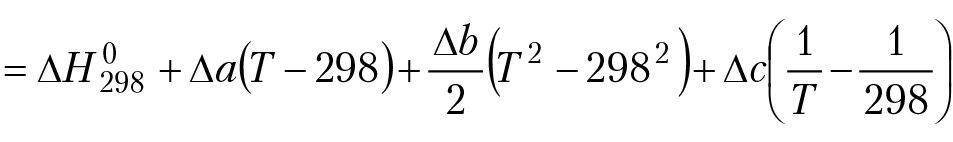 (3.2)
(3.2)
Тепловой эффект реакции, протекающей при постоянном давлении и произвольной температуре, Q°т = – ∆H°т.
3.7. Предмет и основные понятия второго закона термодинамики
Первый закон термодинамики устанавливает количественные соотношения между энергией системы и работой, которая может быть выполнена системой против внешних сил. Совершенно очевидно, что объем выполненной работы не может превышать запас энергии, которым обладает система. Но если предоставить возможность системе непрерывно пополнять запас энергии, например, за счет охлаждения окружающей среды, система может выполнить бесконечно большой объем работы против внешних сил. Но возникает вопрос о возможности реализации любого процесса, не противоречащего первому закону термодинамики (например, пополнение энергии системы за счет охлаждения окружающей среды). Многочисленные наблюдения над природными процессами позволяют утверждать, что теплота не может переходить сама собой от более холодного тела к более горячему и как результат этого закона, невозможно построить такую машину, все действие которой сводилось бы к выполнению работы за счет охлаждения окружающей среды. Эти утверждения носят принципиальный характер и лежат в основе второго закона термодинамики. Тепло самопроизвольно может передаваться только от более нагретого тела более холодному. Таким образом утверждается, что не все процессы, которые не противоречат первому закону термодинамики, могут быть реализованы самопроизвольно. Возникает вопрос, каким образом можно определить, какие процессы могут протекать самопроизвольно, а какие нет? Ответ на этот и подобные вопросы и составляет предмет второго закона термодинамики. Можно сформулировать, что второй закон термодинамики — это учение о вероятности и направлении самопроизвольно протекающих процессов, в частности, учение о процессах, имеющих быть место в природе. Первый, научно обоснованный критерий направленности процессов сформулировал Рудольф Клаузиус (1850):
«Процессы в изолированной системе могут протекать только в таком направлении, чтобы энтропия системы возрастала».
3.8. Энтропия. Определение и физический смысл понятия
Только что мы словами Клаузиуса сформулировали критерий направленности произвольного процесса в изолированной системе, используя понятие энтропии системы. Теперь необходимо уточнить понятие энтропии, т. е. о чем, собственно говоря, идет речь? С исторической точки зрения необходимо отметить, что Клаузиус гениальным образом обобщил работы французского инженера-теплотехника С. Карно и смог показать, что полученные соотношения С. Карно для расчета КПД идеальной тепловой машины можно трактовать как закон перераспределения энергии в изолированной системе. Действительно, если мы включим в состав системы нагреватель, холодильник, рабочее тело, то перераспределение тепла в нашей системе должно подчиняться закону:
где Т2 — температура нагревателя; q2 — тепло, полученное рабочим телом от нагревателя; q1 — тепло, переданное от рабочего тела холодильнику. Рассмотрим процесс теплопередачи с соблюдением правила знаков для теплоты. q2 — это количество теплоты, полученное телом в процессе теплообмена и его надо записывать со знаком плюс; q1 — количество теплоты, которое тело отдает и его надо брать со знаком минус. Следовательно, с термодинамической точки зрения неравенство должно быть переписано следующим образом:
или:
Не составит труда показать, что полученные неравенства остаются справедливыми и в том случае, если в системе имеет место неоднократные процессы теплообмена, т. е. имеет место соотношение
Если в каждой стадии теплообмена количество полученного или отданного тепла мало, q = δq, то в пределе сумма обращается в интеграл: ∫o δq/T , причем ∫o δq/T ≤ 0. Интеграл вычисляется для замкнутого процесса, т. е. параметры системы в начале процесса и в конце совпадают. Проанализируем, что из этого следует. Пусть в процессе теплообмена система переходит обратимым образом из состояния 1 в состояние 2 по пути 1–а–2 (рис. 3.1), а возвращается обратно обратимым образом по произвольному пути 2–b–1. Тогда
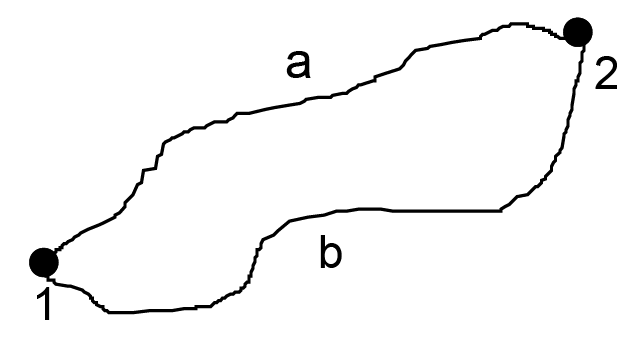
Рис. 3.1. Процесс теплообмена в системе
Мы получили, что
т. е. значение интеграла не зависит от пути перехода системы из одного состояния в другое, а значит может быть представлено в виде разности двух значений некоторой функции состояния системы S,
Под интегральную функцию Клаузиус назвал энтропией системы (S = δq/T), а ∆S — изменение энтропии при переходе системы из одного состояния в другое. Так как изменение энтропии системы не зависит от пути перехода системы из одного состояния в другое, это равносильно тому, что под интегральное выражение есть полный дифференциал: dS = δq/T. Полученные соотношения имеют место для обратимых процессов. В общем случае ∫o δq/T ≤ 0.
Полученное соотношение безусловно точное только для процессов в изолированной системе.
3.9. Изменение энтропии как критерий направленности
и равновесия в изолированной системе
Используя самые общие положения второго закона термодинамики (тепло может самопроизвольно переходить от более нагретого тела к менее нагретому), мы получили, что в случае теплообмена между компонентами системы, должно выполняться неравенство: ∆S ≥ q/T, q — количество тепла, которым тело (или, система тел) обменивается с окружающей средой, Т [К] — температура процесса, ∆S [Дж/моль.°К] — изменение энтропии тела или системы тел, участвующих в термодинамическом процессе. В случае изолированной системы, q = 0, следовательно процессы в изолированной системе могут протекать только в направлении увеличения энтропии, ∆S ≥ 0.
∆S > 0 — критерий направленности процессов в изолированной системе.
Данное утверждение можно рассматривать как одну из формулировок второго закона термодинамики. Необходимо подчеркнуть, что сказанное относится к изолированной системе в целом. В отдельных ее частях возможны процессы с уменьшением энтропии, однако они одновременно должны компенсироваться процессами в других частях системы с ∆S > 0.
Условие равновесия изолированной системы. Второй закон термодинамики предписывает только увеличение энтропии изолированной системы при любых неравновесных процессах в системе. Но такое увеличение энтропии не может продолжаться бесконечно, и когда энтропия достигает максимального значения, это соответствует состоянию равновесия в системе. Действительно, в противном случае энтропия системы должна уменьшаться, что противоречит второму закону. Таким образом, условию равновесия изолированной системы соответствует максимальное значение энтропии системы.
Дальнейшее развитие понятия об энтропии было сделано Л. Больцманом.
3.10. Статистическая интерпретация энтропии Л. Больцмана. Понятие порядка и беспорядка в термодинамической системе
Больцман показал, что энтропия данного термодинамического состояния системы связана с вероятностью состояния системы. Следует отметить, что энтропия описывает состояние системы с термодинамической точки зрения, т. е. характеризует состояние системы в целом. Вероятность состояния системы является статистической характеристикой системы, т. е. определяется значением динамических переменных системы. Для того, чтобы определить динамическое состояние системы, необходимо детально знать положение и движение всех молекул (или компонентов), которые образуют систему. Отсюда следует, что одному термодинамическому состоянию соответствует большое число динамических состояний. В статистической механике принято характеризовать каждое термодинамическое состояние величиной р — числом соответствующих динамических состояний, осуществляющих данное термодинамическое состояние. Число р называют вероятностью данного термодинамического состояния. Так как в системе самопроизвольно протекают наиболее вероятные процессы, это означает, что наиболее устойчивое состояние системы будет состояние с наибольшей вероятность, совместимой с полной энергией системы. Больцман показал, что энтропия системы S и вероятность данного состояния системы Z связаны соотношением: S = k × lnZ; если «w» — вероятность термодинамического процесса, а ∆S — изменение энтропии системы в результате данного процесса, то: ∆S = k lnw (k — постоянная Больцмана). Приведенное соотношение показывает, что изменение энтропии будет наибольшей для наиболее вероятного процесса. Так как наиболее вероятным самопроизвольно протекающим процессом является процесс, который переводит систему в состояние равновесия, то именно в этих процессах наиболее сильно изменяется энтропия. Состояние термодинамического равновесия системы предполагает, что при фиксированных параметрах окружающей среды система как бы замирает, т. е. в системе возможны только незначительные локальные изменения. Положение компонентов в системе должно соответствовать минимально возможной энергии системы, что с точки зрения человека соответствует максимальному беспорядку в данной среде. Так как в процессе движения системы к равновесию энтропия возрастает, поэтому говорят, что энтропия является мерой беспорядка в системе.
3.11. Зависимость энтропии и энтальпии от температуры
Зависимость энтропии от температуры описывается уравнением Кирхгофа, подобное тому, которое мы получили для зависимости энтальпии от температуры: уравнения Кирхгофа:
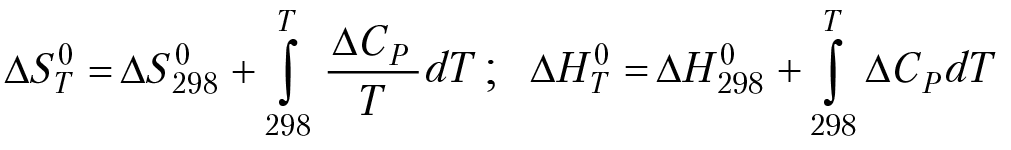 (3.3)
(3.3)
3.12. Расчет изменения энтропии для некоторых термодинамических процессов
Смешение идеальных газов. Запишем уравнения первого и второго законов термодинамики: δQ =∆U + p∆V; ∆S = δQ/T, δQ = T∆S; если в качестве переменных взять давление и температуру, тогда уравнение первого закона можно записать в виде соотношения: δQ = CpdT — V∆p; подставляя значение δQ в первое уравнение, получим объединенное уравнение первого и второго законов термодинамики: TdS = CpdT – VdР. Используя уравнение состояния идеальных газов PV = RT, получим:
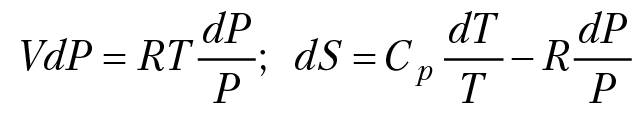
после интегрирования получаем формулу для расчета энтропии одного моля идеального газа: S = S0 + CplnT – Rlgp.
Используя полученные уравнения для расчета энтропии идеального газа, вычислим энтропию смешения n1 молей газа 1 и n2 молей газа 2, находящихся первоначально в двух одинаковых сосудах при одинаковом давлении Р. Если температура газов не изменяется в течение всего процесса, то сумма S0 + CplnT = const и пусть равняется S*. Энтропия первого газа до смешения: S1 = n1(S*1 – RlnP); энтропия второго газа до смешения: S2 = n2(S*2 – RlnP); их суммарная энтропия S до смешения будет равна: S = n1S*1 + n2S*2 – (n1 + n2)R × lgP. Соединяя сосуды, мы получим энтропию газов после смешения:
S12 = n1S*1 + n2S*2 – (n1R×lnp1 + n2Rlnp2).
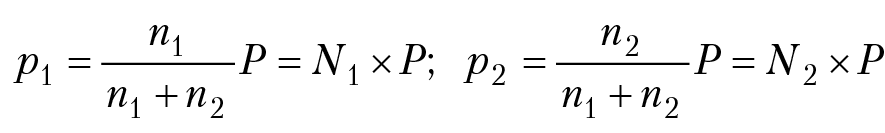
N1 = мольная доля первого газа после смешения, N2 = мольная доля второго газа после смешения. Изменение энтропии после смешения газов ∆S = S12 – S;
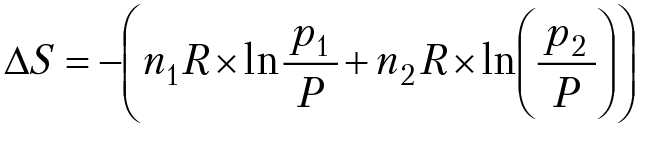
или: ∆S = –(n1RlnN1 + n2RlnN2). Так как N1 < 1 и N2 < 1, то ∆S > 0, т. е. смешение газов идет самопроизвольно! Анализ полученного соотношения для процесса смешения газов ведет к интересному парадоксу, впервые отмеченный Гиббсом: если газы одинаковые, то при открытии перегородки, которая разъединяла газы, никаких термодинамических изменений не должно наблюдаться, т. е. ∆S = 0. Но если есть малейшее различие между газами (например, при смешении изотопов) энтропия смешения скачком переходит от нуля, до ∆S ≠ 0 [∆S = –(n1RlnN1 + n2RlnN2)].
Расчет энтропии при фазовых переходах. Энтропию любого вещества при постоянном давлении можно вычислить по уравнению:
где Cp — теплоемкость вещества при постоянном давлении. Если S0 — энтропия вещества при Т = Т0, тогда изменение энтропии при нагревании вещества (при отсутствии фазового перехода) будет равно:
При фазовом переходе температура постоянная и изменение энтропии можно вычислить по уравнению: ∆S = ∆H°/T0. ∆H° — энтальпия фазового перехода при постоянном давлении, Т0 — температура фазового перехода. Вычислим изменение энтропии при превращении одного моля льда в пар при постоянном внешнем давлении один бар и начальной температуре — 20 °С. В этом процессе мы имеем дело с двумя фазовыми переходами: превращение льда в воду при температуре 0 °С (273 °К) и превращение воды в пар при 100 °С (373 °К). При нагревании льда надо иметь ввиду, что теплоемкость льда (Ср)лед линейным образом зависит от температуры: Ср = 1,1803 + 0,131Т (Дж/моль×К). Изменение энтропии при нагревании льда от –20 °С до 0 °С будет равно:
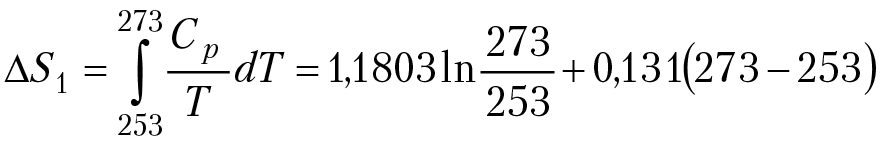
∆S1 ≈ 2,69 (Дж/моль×К).
Энтальпия плавления льда 6031(Дж/моль), следовательно, ∆S2 = ∆H°/T = 6010/273 = 22,01 (Дж/моль×К).
Приращение энтропии при нагревании воды 0 °C до 100 °С:
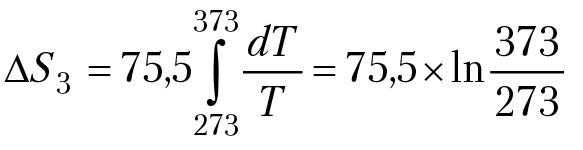
∆S3 = 23,56 (Дж/мольК); при условии, что Ср = const.
Энтальпия испарения воды при T = 100°C, ∆Н° = 40656(Дж/моль). Изменение энтропии: ∆S4 = ∆Н/Т = 40 656 : 373; ∆S4 = 109 Дж/моль×К). Полное изменение энтропии при нагревании льда равно: ∆S = ∑∆Si = 157,26 (Дж/моль×К).
3.13. Тепловая теорема Нернста (третье начало термодинамики)
Тепловая теорема Нернста характеризует общие закономерности поведения вещества вблизи абсолютного нуля температуры. При анализе зависимости термодинамических функций от температуры возникает проблема вычисления абсолютного значения термодинамической функции. Например, закон изменения энтальпии реакции от температуры описывается уравнением:
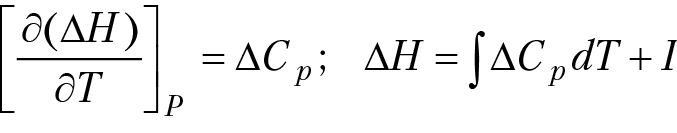
При вычислении интеграла обязательно появляется постоянная интегрирования “I”. Вычислить постоянную интегрирования из общих соображений (например, на основании первого или второго законов термодинамики) нельзя.
Такая же проблема возникает и при расчетах температурной зависимости изобарного потенциала реакции и энтропии:
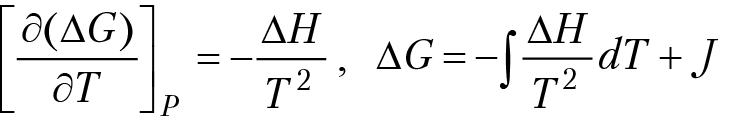
∆S = ∫∆Н + Y. Эту трудность частично можно обойти, если знать зависимость теплоемкости компонентов реакции от температуры и значение термодинамической функции при одном из допустимых значений температуры. Например, при вычислении энтальпии реакции мы постулируем значение энтальпии реакции при Т = 298 °К и Р = 1 бар: ∆Н°298;
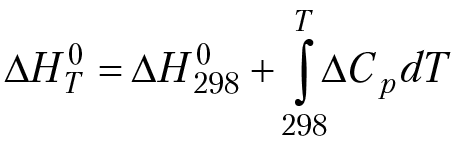
Но мы не можем выполнить интегрирование во всем температурном интервале, от Т = 0 °К до Т = Т °К, так как поведение теплоемкости вещества вблизи абсолютного нуля подчиняется законам квантовой механики и не может быть получена на основании термодинамических соображений. Опыт показывает, что по мере приближения к абсолютному нулю свойства вещества все менее зависят от температуры, в частности, теплоемкость вещества стремится к нулю. Область температур, в которой проявляются особые свойства вещества, у различных веществ разная. Например, для алмаза теплоемкость практически равна нулю, ниже 90 °К, для свинца — 1,6 °К. Это означает, что алмаз при 10 °К, приведенный в соприкосновение с газом, имеющим температуру 80 °К, не будет нагреваться. Следствием такого свойства вещества вблизи абсолютного нуля является тот факт, что обязательно должен существовать температурный интервал, не равный нулю, внутри которого термодинамические функции не зависят от температуры а для энтальпии и изобарного потенциала реакции вблизи Т~ 0 °К выполняются соотношения:
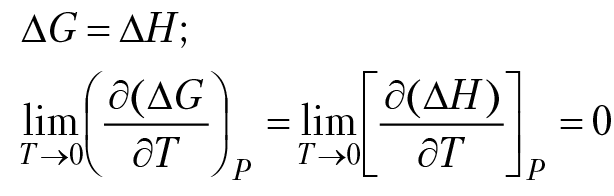
На рисунке 3.2 приведена зависимость энтальпии изобарного потенциала реакции от температуры. Необходимо обратить внимание на то, что вблизи абсолютного нуля существует не равный нулю температурный интервал ∆Т, внутри которого термодинамические функции не зависят от температуры и их значения равны друг другу. В заключение сформулируем тепловую теорему Нернста и основные понятия третьего закона термодинамики.
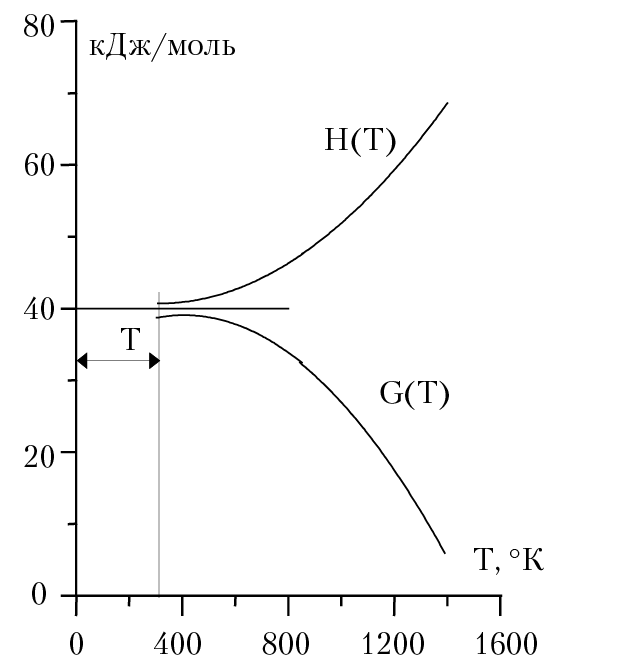
Рис. 3.2. Зависимость ΔH и ∆G от температуры
Для процессов, протекающих в конденсированных системах, при приближении температуры к абсолютному нулю кривые изобарного потенциала и энтальпии соединяются и имеют общую касательную, параллельную оси температуры.
Тепловую теорему Нерста необходимо дополнить постулатами Планка: энтропия правильно образованного кристалла при абсолютном нуле температуры равна нулю. Вблизи абсолютного нуля теплоемкость правильных кристаллических веществ равна нулю.
Правильно образованный кристалл — это такой кристалл, все узлы которого заняты лишь атомами или молекулами данного вещества и отсутствуют дефекты кристаллической решетки. Отметим, что первый постулат Планка можно считать следствием из соотношения Больцмана для энтропии вещества: энтропия S вещества пропорциональна термодинамической вероятности w существования вещества: S = klnw, которая в свою очередь определяется числом макросостояний, которым может быть реализовано состояние вещества. Так как частицы, составляющие правильный кристалл, могут быть размещены единственным образом, поэтому w =1, а S = 0.
Вывод: предметом третьего закона термодинамики является учение о тепловых свойствах вещества вблизи абсолютного нуля. Содержание третьего закона составляют тепловая теорема Нернста и постулаты Планка.

