Физическая химия

1.1. Способы описания движения материи

1.2. Основные этапы развития теории строения атома

1.3. Строение атома по Н. Бору. Атом водорода

1.4. Успехи и принципиальные затруднения теории Н. Бора

1.5. Корпускулярно-волновой дуализм. Волны де Бройля. Принцип неопределенности В. Гейзенберга

1.6. Квантомеханический метод описания движения частицы. Волновая функция. Уравнение Э. Шреденгера

1.7. Уравнение Э. Шредингера для атома водорода

1.8. Периодическая система элементов Д. И. Менделеева

1.9. Местонахождение электрона в атоме

1.1. Способы описания движения материи

Движение частиц от очень больших размеров (например, галактики) до очень маленьких (элементарные частицы) описывается в разделах механики, которые мы называем как классическая, релятивистская, квантовая механика.

Классическая механика. Основные понятия классической механики были разработаны И. Ньютоном и Дж. Гамильтоном. Механика Ньютона исторически была первой разработанной системой понятий и законов, развитие которой привело к созданию того, что мы называем физикой. Основанная на наблюдениях за движением обычных тел в повседневной жизни, классическая механика нашла успешное применение при описании движения этих тел и их взаимодействий. При этом механика имела дело с материальными телами, которые по своим размерам, с одной стороны, не были сверхбольшими, как галактики или нейтронные звезды, а с другой стороны, не были такими малыми, как атомы. В основу модели механики Ньютона положены векторные величины — сила и импульс. Отметим, что при рассмотрении классической задачи о движении частицы ее масса m считается постоянной и уравнения движения получают интегрированием уравнения: m(d2r/dt2) = ∑fi; r — радиус-вектор, соединяющий начало инерциальной системы координат с движущейся частицей. В механике Гамильтона в основу механической модели движения материи положено понятие энергии взаимодействия частиц. Пусть частица под действием внешних сил перемещается из точки А в точку B за время t = t2 – t1 по одной из возможных траекторий движения. Тогда интеграл

вдоль истинной траектории движения имеет минимальное значение. T(t, x, y, z) кинетическая энергия частицы в точке (xyz), U(t, x, y, z) — потенциальная энергия взаимодействия частицы с окружающим ее материальным миром. Функция L = T – U называется функция Лагранжа. Реальная траектория движения частицы определяется варьированием функции Лагранжа. Можно показать, что законы Ньютона могут быть получены из принципа Гамильтона и наоборот. Отметим, что законы классической механики находятся­ в полном соответствии с принципом относительности Галилея, который­ предполагает­ одновременность события (если произошло событие, то оно произошло для всех наблюдателей одновременно!). В релятивистской механике принцип одновременности события может не выполняться. Отметим, что одним из основных понятий классической механики является понятие о траектории движения частицы.

Релятивистская механика. Рассмотрим теперь задачу о движении тел со скоростями, которые соизмеримы с предельной скоростью взаимодействия тел — со скоростью света. В этом случае мы должны применить модель механики, связанную с общей теорией относительности. Если наложить определенные ограничения на движение тел (например, чтобы скорости тел менялись достаточно плавно) мы придем к модели механики, которая называется специальной теорией относительности [СТО] (А. Эйнштейн, 1905). Особенность движения тел, которое описывается СТО, связана с зависимостью инерционной массы тела, длины отрезка и хода часов от скорости движения тела. Эти положения СТО не имеют классической аналогии и связаны с одной единственной гипотезой: невозможно движение тела со скоростью, превышающей скорость света в вакууме. Но для вновь построенной механики обязательно должен выполняться принцип соответствия (Н. Бор, 1923): всякая новая теория в физике должна сводиться к хорошо установленной классической теории, если эта теория прилагается к специальным случаям, которые успешно описываются менее общей теорией. Если в формулах СТО сделать предельный переход lim u/c = 0 (u — скорость движения частицы, с — скорость света), то законы движения СТО переходят в законы движения классической механики.

Квантовая механика. Квантовая механика, принципиально отличающаяся от рассмотренных моделей, создана для исследования поведения систем микромира. Здесь следует отметить, «что частицы вещества, например электроны, не могут внутри объектов атомного масштаба совершать все движения, описываемые классической механикой; физически возможными оказываются лишь некоторые движения, удовлетворяющие квантовым условиям, в которых фигурируют целые числа и постоянная Планка» [Луи де Бройль. По тропам науки]. Существуют две эквивалентные (но разные по форме) модели квантовой механики, разработанные В. Гейзенбергом и Э. Шредингером. Релятивистское решение задач квантовой механики, выполненное П. Дираком, привело к открытию антивещества. Основные понятия, которые легли в основу квантовой механики, связаны с понятиями квантования, корпускулярно-волнового дуализма и принципом неопределенности. Пионерами в создании квантовой механики были Макс Планк и Нильс Хенрик Дейвид Бор. Современное здание квантовой механики возникло благодаря работам Шредингера, Гейзенберга, Дирака, Паули и др. выдающихся физиков.

1.2. Основные этапы развития теории строения атома

К концу XIX столетия полностью оформилось стройное и красивое здание классической физики. Законы, сформулированные Ньютоном и Максвеллом, точно и четко описывали гравитационные и электромагнитные взаимодействия в мире макроскопических ча­стиц и в той части Вселенной, которая была доступна для изучения физикам тех дней. Практически все разделы физики были детально исследованы и только отдельные вопросы пока не имели ответа. Одними из таких нерешенных задач была проблема излучения энергии раскаленным твердым телом и строение атома. Несмотря на все попытки физиков дать полное объяснение экспериментальным фактам на основе классической физики, решение задач не было найдено. Первая задача была разрешена на основании корпускулярной теории излучения М. Планка, причем решение задачи оказалось совершенно неожиданным. На основании электромагнитной теории Максвелла, считалось, что излучение и поглощение энергии телом имеет волновую природу и является результатом взаимодействия колебаний линейных гармонических осцилляторов раскаленного тела (связанных электрических зарядов, подобных диполям).

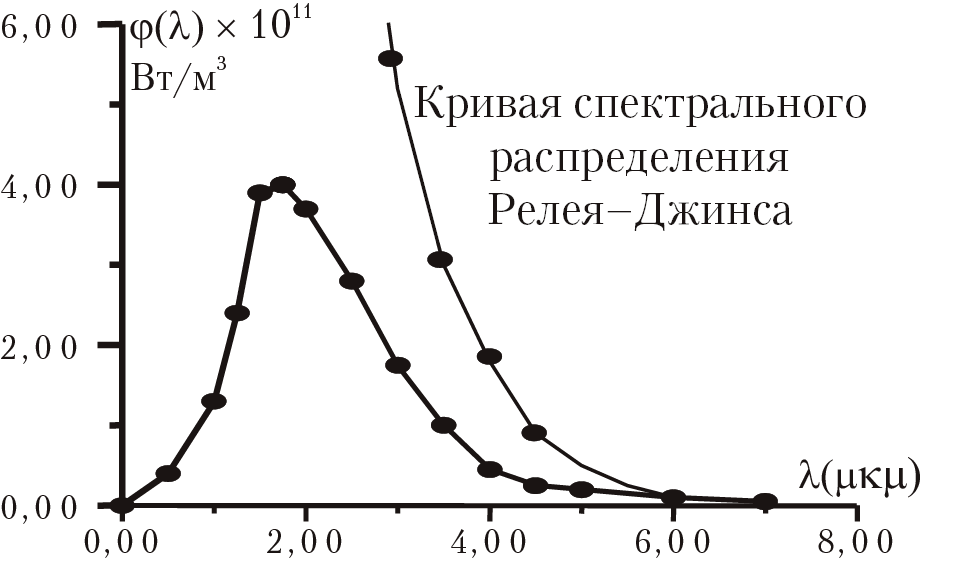
Рис. 1.1. Спектральное распределение излучения твердого тела при 2000 К

На основании таких представлений был получен закон распре­деления излучения Релея–Джинса: φ (λ, Т) – (2 π c / λ4)kT; c — скорость света. К сожалению, формула Релея–Джинса давала относительно хорошее согласие с опытом только в области длинных волн спектра излучения; в области УФ-излучения формула Р–Д была совершенно не корректна. Учитывая все эти трудности и обобщая многочисленные экспериментальные данные, Макс Планк сформулировал принципиально новые законы взаимодействия вещества с излучением: 1) разогретое тело не излучает свет непрерывно. Излучение или поглощение энергии происходит только в момент изменения амплитуды колебания осциллятора; 2) осциллятор может испускать или поглощать энергию только определенными порциями, так называемыми квантами. Энергия кванта ε = hν, h (постоянная Планка) – 6,626 × 10–34 (Дж × сек), ν(Гц) — частота излучения. 14 октября 1900 г., на заседании Берлинского физического общества, М. Планк доложил результаты своих экспериментальных и теоретических исследований по проблеме взаимодействия электромагнитного излучения с веществом. М. Планк предложил принципиально новый подход к проблеме и вывел новый закон распределения энергии в спектре излучения раскаленного тела:

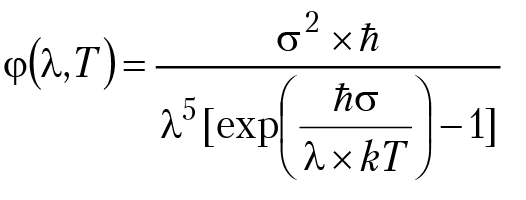
где σ = 2πc; c — скорость света, ħ = h/2π.

Гипотеза М. Планка о квантах электромагнитного излучения оказалась исключительно плодотворной и положила начало новому этапу в развитии физики. Но оставалась проблема строения атома. Каким образом связаны осцилляторы Планка и структура атома?

Строение атома. Модель атома Дж. Дж. Томсона. После теории излучения, второй проблемой, которая оказалась непосильной для классической физики, была проблема строения атома. В 1903 г. английский физик Дж. Томсон предложил модель атома, согласно которой атом представляет собой равномерно заполненный положительным электричеством шар, внутри которого находятся электроны. Согласно описанной модели, электроны в атоме будут совершать гармонические колебания с частотой ω ≈ 3 × 1015 Гц, что соответству­ет красному участку видимого спектра излучения. Оценка размеров атома (≈ 3 × 10–8 см) хорошо совпадала с ранее полученными экспериментальными данными, что можно было бы рассматривать как подтверждение модели. Но эксперименты Эрнеста­ Резерфорда по рассеиванию α-частиц атомами однозначным образом разрушили теорию атома, предложенную Дж. Томсоном.

Ядерная модель атома. Проанализировав результаты рассеивания α-частиц атомами, Резерфорд пришел к выводу, что положи­тельный заряд атома сосредоточен в очень маленьком объеме (≈10–42м3) и связан с веществом с большой плотностью. Основываясь на этих экспериментальных данных, Резерфорд предложил ядерную модель атома, согласно которой атом представляет собой систему зарядов, в центре которой расположено тяжелое положительно заряженное ядро с зарядом Ze, а вокруг ядра, по всему объему атома располагаются электроны. Однако ядерная модель оказалась в противоречии с законами электродинамики. При движении электронов в атоме, атом должен непрерывно излучать энергию, а это должно привести к падению электронов на ядро, т. е. к разрушению атома. В конечном итоге оказалось, что любая модель атома в сочетании с классической физикой, неспособна объяснить ни устойчивость атома, ни характер спектра излучения атома. Выход из создавшегося тупика был частично найден в 1913 г. датским физиком Нильсом Бором.

1.3. Строение атома по Н. Бору. Атом водорода

Теория строения атома по Бору основана на двух постулатах. В основе первого постулата лежит утверждение, что электроны вращаются вокруг ядра по стационарным орбитам, не излучая и не поглощая энергию. Излучение и поглощение энергии атомом происходит при переходе электронов с одних стационарных орбит на другие. Энергия излучения определяется соотношением: w = w2 – w1; w1 — энергия атома в основном состоянии, w2 — в возбужденном состоянии. В теории Бора изменение энергии атома связана с изменением энергии электронов в атоме. Второй постулат в теории Н. Бора касается уравнения движения электронов в атоме. Его можно сформулировать следующим образом: стационарные орбиты электронов в атоме это такие, на которых момент импульса электрона равен целому числу постоянных Планка, деленной на 2π: m[u×r] = nħ, n = 1, 2, 3. В данной формуле и в дальнейшем изложении ŋ = h/2π = 1,05 10–34(Дж×сек), m = 9,1 × 10–31 кг (масса электрона), u — скорость электрона на орбите радиуса r, [r] = м. Таким образом, Н. Бор предложил для электрона в водородоподобных атомах уравнения движения:

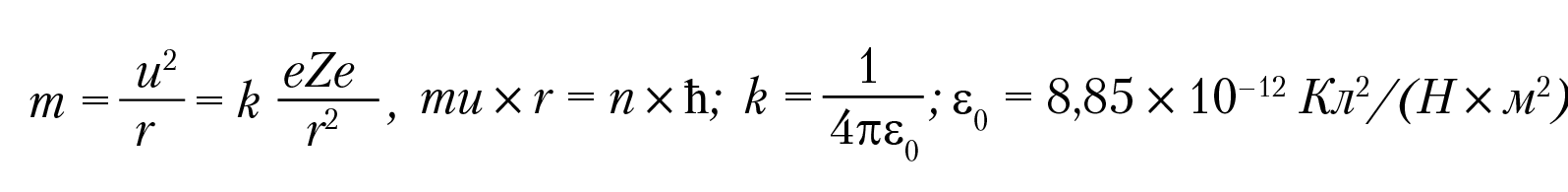
e = 1,6 × 10–19 Кл, Z×e — заряд ядра. Для водорода Z = 1, радиусы боровских орбит: r = 4πε0ħ2/me2, n = 1, 2, 3; для n = 1 (первая боровская орбита), получим: r = a0 = 0,53 A Единица длины 10–8 см называется ангстрем и обозначается Å : 1Å = 1 × 10–8 см. Энергия атома складывается из потенциальной энергии взаимодействия электрона с ядром U и кинетической энергии вращения вокруг ядра T:

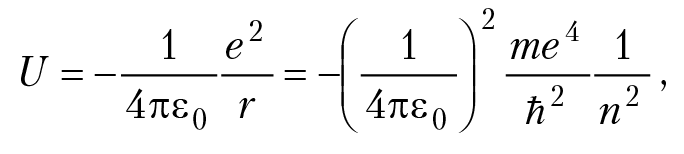
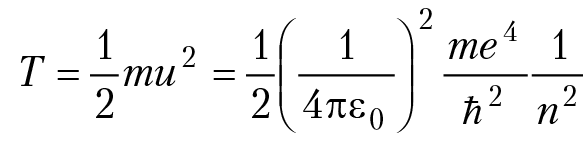
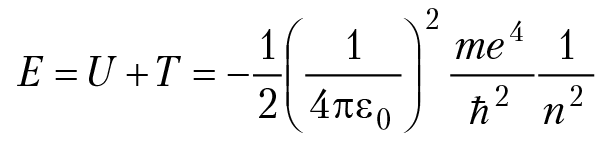
Так как радиус первой боровской орбиты электрона в атоме водорода

выражение для полной энергии электрона в атоме водорода можно записать:

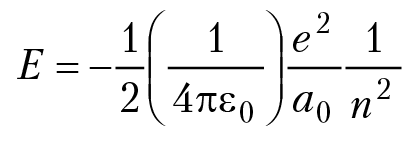
n = 1, 2, 3… В спектроскопии выражение

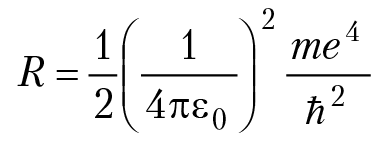
называют постоянная Ридберга (в честь шведского физика И. Ридберга); R = 13,6 эВ (1 Дж = 1,6 × 10–19 эВ). Е = –13,6/n2 эВ.

Задача 1.1 Какую энергию надо сообщить электрону, чтобы перевести его с орбиты n = 1 на орбиту с n = 2.

Решение. E2(n = 2) – E1(n = 1) = 0,75 × 13,6 эВ. Если эту энергию сообщить электрону в виде электромагнитного излучения, то длина волны источника излучения должна быть равна: hν = E2 – E1, (h × c) λ = ∆E, λ = (c×h)/∆E ; λ = 1220 A, жесткий ультрафиолет.

Проверить полученные формулы можно из анализа оптических спектров поглощения и испускания. Экспериментальное исследование оптических спектров водорода и водородоподобных атомов подтвердили справедливость полученных формул.

Спектр атомарного водорода:	λ × 108 см
Серия Лаймана: эксперимент	1215,7 1025,7;
расчет:	1218 998

1.4. Успехи и принципиальные затруднения теории Н. Бора

Теория строения атома, предложенная Н. Бором, была первой теорией, которая объяснила основные черты поведения электронов в атомах и предложила алгоритмы для количественных расчетов основных параметров структуры атомов. Теория Н. Бора объяснила природу возникновения света, как квантовый процесс перехода электронов из возбужденного состояния в стационарное, оценила размеры атома, объяснила магнитные и оптические свойства атома водорода. Но Н. Бор сделал только полшага в создании теории строе­ния атома. Теория Бора была основана на правильных (постулаты Бора) и неправильных (классические уравнения движения, понятиях о траектории движения электронов и т. д.) утверждениях. По этой причине соответствующие расчеты приводили то к правильным, то к неправильным результатам, причем никогда нельзя было знать заранее, какой результат окажется правильным, а какой ошибочным. Количественное изучение тонкой структуры оптических спектров привело к установлению ряда новых фактов, которые не поддаются простой трактовке в рамках теории Бора, часто находясь в явном противоречии с выводами теории. Например, согласно теории Н. Бора пучок атомов любого элемента первой группы в неоднородном магнитном поле будет расщеплен на три пучка, в то время как в действительности наблюдается раздвоение пучка. Непреодолимые трудности встретила теория Н. Бора в случае объяснения свойств атома гелия, аномального эффекта Зеемана. Затруднения теории Бора, встретившиеся на пути объяснения тонких деталей строения и свойств атома, явились лишь частным проявлением несостоятельности полуклассического подхода в описании микроскопических явлений. Ряд новых открытий в области физики микромира и в первую очередь открытие волновых свойств материи, потребовали создания принципиально новой модели механики — квантовой механики, в основе которой лежал бы дуализм материи.

1.5. Корпускулярно-волновой дуализм. Волны де Бройля.
Принцип неопределенности В. Гейзенберга

Первым толчком в создании волновой (квантовой) механики послужили идеи Луи де Бройля (1924), применившим эйнштей­новскую идею корпускулярно-волнового дуализма света к материальным частицам. В области света корпускулярно-волновой дуализм возник в связи с тем фактом, что вся совокупность световых явлений не могла быть объяснена лишь с точки зрения волновой или корпускулярной теории. Анализируя явление фотоэффекта, рассеи­вания света на электронах (эффект Комптона), мы представляем себе свет в виде потока световых корпускул или фотонов, характеризующихся энергией ε = hν (М. Планк) и количеством движения p = hν/c (А. Эйнштейн). С точки зрения волновой теории и на основании экспериментов по дифракции и интерференции света, тот же самый свет мы представляем себе в виде волн, характеризуя их длиной волны λ или частотой ν = c/λ. Такая двойственная природа света (корпускулярная и волновая) позволила А. Эйнштейну сформулировать понятие о корпускулярно-волновом дуализме света. Перенося корпускулярно-волновые представления в область материальных частиц, французский физик де Бройль высказал ги­потезу о том, что каждой движущей частице может быть сопоставлена некоторая волна с λ = h/p, где p = m × u (импульс частицы). Согласно гипотезе де Бройля, перемещение микрочастиц в пространстве следует рассматривать и как движение частицы и как волновое движение (аналогия со светом). В частности, движение электрона в пространстве со скоростью, много меньшей скорости света, следует описывать как движение частицы с массой m = 9,1 × 10–31 кг и зарядом q = 1,6 × 10–19 Кл и как распространение электромагнитной волны с; λ [A°] = h/mu = 7281 × 103/u; u[м/сек] — скорость электрона. Уже при скорости u = 1000 м/сек, с электроном ассоциируется волна с λ ≈ 7000 Å. Отметим, что для частицы с массой ≈ 1мкг = 10–9 кг длина волны де-Бройля будет чрезвычайно мала: λ = 6,63 × 10–34/mu = 6,63 × 10–25/u (м), [u] = м/сек. Естественно поэтому, что волновые свойства макро- и микрочастиц никогда не были обнаружены, так как волновые свойства проявляют себя на расстояниях, сравнимых с длиной волны частицы. В гипотезе де Бройля были сформулированы принципиально новые понятия о поведении в пространстве частиц, массы которых сравнимы с массой атома и это потребовало создания новой механики для описания движения таких частиц (она была названа волновой механикой) и постановки совершенно необычных экспериментов для проверки правильности новых гипотез о строении вещества. Например, для волнового движения характерно явление интерференции волн. В 1927 г. американские физики Девиссон и Джермер в опытах по рассеиванию электронов на кристаллах никеля получили интерференционную картину, соответствующую интерференции света в рентгеновском диапазоне. В данных экспериментах электроны разгонялись в электрическом поле с разностью потенциалов ∆φ = 50 в. Согласно формуле де Бройля, в этих экспериментах электронам соответствует длина волны λ ≈ 1,75 Å. Эксперименты по рассеиванию рентгеновских лучей с λ = 1,8 Å на кристаллах никеля дали такую же интерференционную картинку, как и в случае рассеивания электронов на кристаллах никеля, что блестяще подтверждает гипотезу де Бройля. В том же 1927 г. Гейзенберг сформулировал фундаментальное соотношение между координатами микрочастицы и ее импульсом:

∆x∆px ≥ 2πħ; ∆y∆py ≥ 2πħ; ∆z∆pz ≥ 2πħ; ħ = h/2π

(ошибка в одновременном измерении координаты микрочастицы и проекции ее импульса на эту координату всегда больше по­стоянной Планка). Соотношение неопределенностей заставляет отказаться от понятия траектории движения частицы: если мы с максимальной точностью определим положение микрочастицы, то сделаем большую ошибку в определении импульса частицы, т. е. направления движения частицы. Но если нет возможности определить направление движения частицы, значит нет смысла говорить о траектории движения частицы. Можно говорить только о вероятности нахождения микрочастицы в данной точке пространства. Данное соотношение выражает один из фундаментальных законов физики микромира и полностью соответствует гипотезе де Бройля. Классическая физика исходит из предопределенности мира. Она считает, что если одновременно измерить координаты и импульсы всех атомов, то, применяя физические законы, можно было бы рассчитать состояние всех атомов (т. е. полную картину мира) на любой промежуток времени вперед и назад. Квантовая механика утверждает, что рассчитать можно только вероятности, но нельзя предсказать, какая из возможностей в конце концов осуществится. Какая из возможностей будет реализована — дело случая, и эта неопределенность возникает не вследствие несовершенства физических теорий, а вытекает из существа законов, действующих в микромире и правильно отражаемых наукой. Новые понятия породили и новую, квантовую механику описания движения частиц.

1.6. Квантомеханический метод описания движения частицы.
Волновая функция. Уравнение Э. Шреденгера

Попытки описать движение электрона в атоме, принимая во внимание только корпускулярные свойства частицы, потерпели неудачу. В свете новых понятий о свойствах частицы (дуализм частиц) была предпринята исключительно удачная попытка учесть в одном уравнении волновые и корпускулярные свойства частицы. Именно эта попытка и реализована в квантовой механике. Основными характеристиками волнового процесса являются повторяемость (периодичность) проявления каких-то свойств, скорость распро­странения волны u, длина волны λ или частота колебания ν (они связаны соотношением: λ × ν = u), период колебания T = 1/ν.

Основные характеристики движения микрочастицы могут быть получены из анализа волнового уравнения микрочастицы. В качестве примера рассмотрим, как можно получить волновое уравнение, которое­ описывает поперечные волновые колебания частицы. Пусть поперечный колебательный процесс распространяется в направлении от А → В, рис. 1.2. Так как мы рассматриваем поперечные колебания (т. е. периодические изменения свойств системы наблюдаются в направлении, перпендикулярном направлению распространения волны; таким свойством обладают, например, электромагнитные волны­), то когда волна достигнет точки N, находящейся на расстоянии х, от А (это произойдет через время t = х/u, где u (м/сек) — скорость распространения волны) к этому моменту точка N займет положение N1: NN1 = φ (смещение N от положения равновесия); в случае гармонического колебательного процесса, изменения φ (волновая функция колебательного процесса) φ = asin[2π(νt – x/λ)] будет в этом случае удовлетворять волновому уравнению

(для одномерного случая). Чтобы получить это волновое уравнение, достаточно вычислить вторые частные производные от волновой функции по переменным (x, t). В общем случае, для трехмерного процесса волновое уравнение имеет вид: ∆φ = (–4π2/λ2)φ; ∆ — оператор Лапласа, обозначающий, что от функции φ необходимо взять сумму вторых частных производных по x, y и z: ∆ = д2/дх2 + д2/дy2 + д2/дz2. С помощью полученного уравнения и его решения, волновой функции, можно проанализировать колебания струны, поведение молекул воды на поверхности моря, распространение световой волны и т. д.

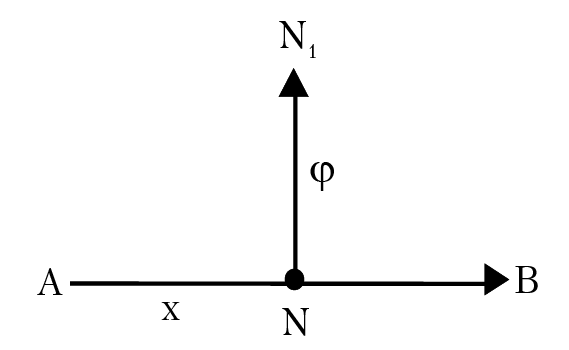
Рис. 1.2. Схема распространения поперечной волны

1.6.1. Уравнение Э. Шредингера

Теперь представим, что при описании волнового процесса необходимо принять во внимание корпускулярные свойства частицы. Формально это можно сделать, если в уравнение, которое описывает волновой процесс ∆φ = (–4π2/λ2)φ для длины волны подставить со­отношение де Бройля λ = h/mu, а скорость частицы вычислить из соотношения mu2/2 = E – U; где E — полная энергия частицы, U — потенциальная энергия частицы. Выполнив соответствующие­ подстановки, получим основное уравнение нерелятивистской квантовой механики, предложенное Э. Шредингером в 1926 г.:

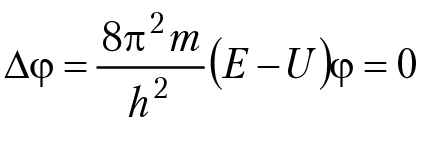
где U — потенциальная энергия частицы, E — полная энергия частицы, ∆ — оператор Лапласа, φ — волновая функция частицы, энергия ко­торой равна E. В квантовой механике уравнение Э. Шредингера играет такую же фундаментальную роль, как уравнения движения Ньютона и уравнения электродинамики Максвелла. С математической точки зрения уравнение Э. Шредингера подобно уравнению, описывающему, например, колебания струны. Но трактовка решения волнового уравнения для струны ∆φ = (–4π2/λ2)φ и уравнения Э. Шредингера для частицы ∆φ = (8π2m/h2)(E – U)φ = 0 принципиально различны. В отличие от решения уравнения колебания струны, которое задает геометрическую форму струны, решение уравнения Э. Шредингера (волновая функция φ(x,y,z)), прямого физического смысла не имеет. Согласно М. Борну, смысл имеет квадрат модуля волновой функции |φ(x,y,z)|2 dV, равный вероятности нахождения частицы в данном квантовом состоянии в точке пространства с координатами x, y, z и в элементе объема dV = dx × dy × dz. Полученное уравнение Э. Шредингера связывает волновое описание процесса с корпускулярными свойствами частицы.

1.6.2. Описание движения частицы методами квантовой механики

Рассмотрим особенность описания движения частицы методами квантовой механики и сравним это описание с классическим решением задачи. В качестве примера рассмотрим равномерное движение частицы с массой m вдоль оси ОХ; движение частицы ограничено непроницаемыми стенками, координаты которых x = 0 и x = d; пусть потенциальная энергия частицы U(x) равна нулю на отрезке 0 ≤ x ≤ d и обращается в бесконечность (U(x) = ∞) за пределами отрезка [0, d]. В этом случае говорят, что частица находится в «потенциальной яме», так как полная энергия частицы за пределами ямы меньше ее потенциальной энергии: E = mV2/2 < U. Рассмотрим вначале классическое описание движения частицы. На отрезке 0 ≤ x ≤ d она движется с постоянной скоростью V0 и кинетической энергией Ei = mV 20i/2. Энергия частицы в яме может иметь любое значение, так как мы можем задать любую скорость движения частицы; уравнение движения частицы предельно простое: x = V0 × t. Подойдя к краю ямы, частица упруго отражается от стенки и движется в противоположную сторону, там снова отражается и т. д.

Описание движения частицы методами квантовой механики. В первую очередь отметим, что описание движения частицы методами квантовой механики, имеет смысл только в том случае, если длина волны частицы (в смысле соотношения де-Бройля) соизмерима с размерами потенциальной ямы λ ≈ d (d — длина отрезка [0,d]). Это соотношение накладывает серьезные ограничения на физические параметры частицы. Разберем данное положение подробнее. Так как λ = h/mV0, квантомеханическое рассмотрение движения частицы имеет смысл, если импульс частицы и линейные размеры потенциальной ямы связаны соотношением mV0 ≈ h/d, λ ≈ d; такой импульс может иметь, например, электрон при движении в потенциальной яме размером в 1 см со скоростью ≈ 1 см/сек. В этом случае энергия частицы Е ≈ 10–34 Дж. Продолжаем анализ движения частицы методами квантовой механики. Теперь нам необходимо записать уравнение Э. Шредингера для частицы в потенциальной яме. Пусть φ(х) — волновая функция частицы; уравнение Э. Шредингера в случае одномерного движения частицы вдоль оси ОХ имеет вид:

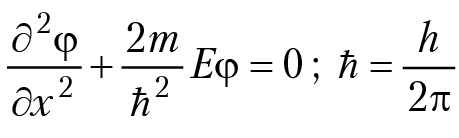
Е — полная энергия частицы; решением уравнения Э. Шредингера будет функция φ = A sin[ωx + β], где

в этом легко убедиться непосредственной проверкой. Волновая функция частицы φ = Asin[ωx + β] должна быть непрерывной (так как она описывает движение частицы во всех точках интервала (0,d) и равна нулю в точках x = 0 и x = d. Из условия φ(0) = 0 следует, что β = 0; из условия, что φ(d) = 0, получаем ω = ±πn/d, n = 1, 2, 3...; энергия частицы

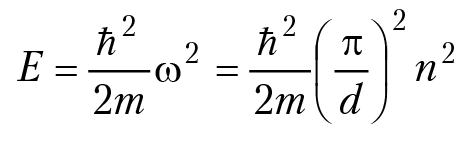
волновая функция частицы:

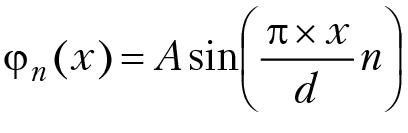
теперь необходимо определить значение константы А. Так как в любой момент времени частица находится на оси ОХ в пределах интервала (0, d), вероятность нахождения частицы в пределах интервала 0 < x < d должна быть равна единице:

(условие нормировки волновой функции);

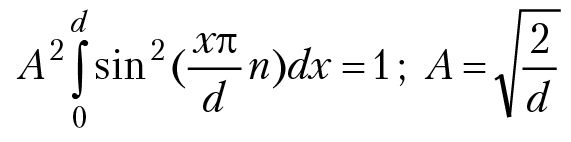
Окончательно нормированные собственные волновые функции частицы имеют вид:

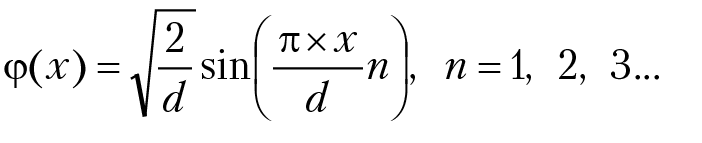
Сделаем анализ полученных результатов. Принимая во внимание корпускулярно-волновые свой­ства частицы, мы поставили задачу описать движение частицы методами квантовой механики. Согласно законам квантовой механики, мы записали уравнение Э. Шредингера для частицы

и нашли его решение — волновую функцию

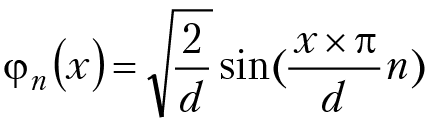
и значение энергии частицы:

n = 1, 2, 3...; и первая неожиданность — спектр значений энергии оказался дискретным! Расстояние между уровнями энергии:

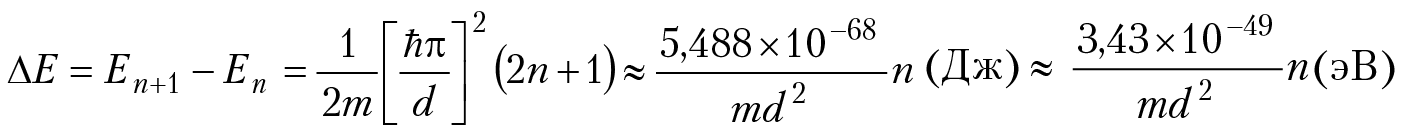
Оценим дискретность уровней энергии, например, для молекул газа в сосуде диаметром d ≈ 10 см. Если масса молекулы m ≈ 10–26 кг, то ∆Е ≈ 10–21 × n (эВ). Столь густо расположенные энергетические уровни можно рассматривать как сплошной спектр, т. е. считать, что энергия молекул газа плавно возрастает при переходе в возбужденное состояние (отсутствует квантование энергии). Однако совсем другой результат получается, если провести анализ движения электрона в пределах атома или молекулы, т. е. если d ≈ 10–10м, m = 9 × 10–31 кг. В этом случае ∆Е ≈ 38 × n эВ, т. е. дискретность энергетических уровней (квантование энергии) частицы будет весьма заметной для возбужденных состояний частицы. Далее: сделаем анализ положения частицы в пространстве. Как известно, вероятность положения частицы в точке с координатой х ± ∆x (для одномерного случая) равна:

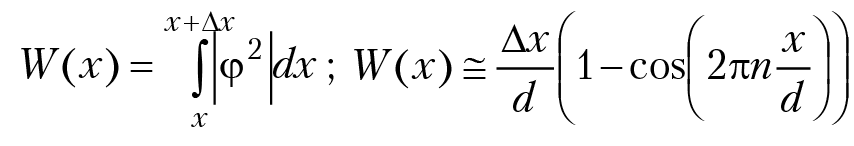
плотность вероятности P(x) обнаружить частицу в точке с координатой х будет равна:

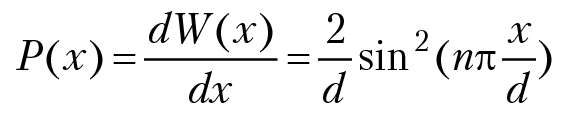
На рисунке 1.3 дана плотность вероятности обнаружения частицы в зависимости от координаты точки, где мы предполагаем нахождение частицы. Например, при n = 2, в точке с координатой х = 0,5 частица не может быть обнаружена! с другой стороны, в точках с координатами 0,25 и 0,75 частица может находится с максимально большой и равной вероятностью! рис. 1.3 Такое поведение частицы несовместимо с понятием траектории движения частицы. С классической точки зрения, частица в любой момент времени должна находится на прямой линии и ее можно обнаружить в окрестности любой точки ∆х с равной вероятностью Wкл = ∆x/d (d — длина классической траектории движения частицы). Отметим, что с ростом осцилляций (или нулей функции φ2(х)) возрастает вероятность нахождения частицы в любой точке траектории , так что при больших n максимумы и минимумы кривой следуют друг за другом столь тесно, что мы придем к классической формуле для расчета вероятности нахождения частицы на отрезке [0,d].

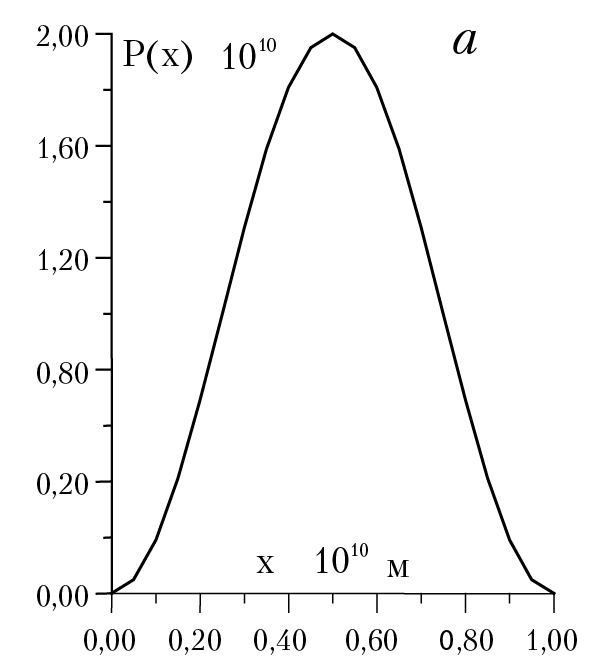
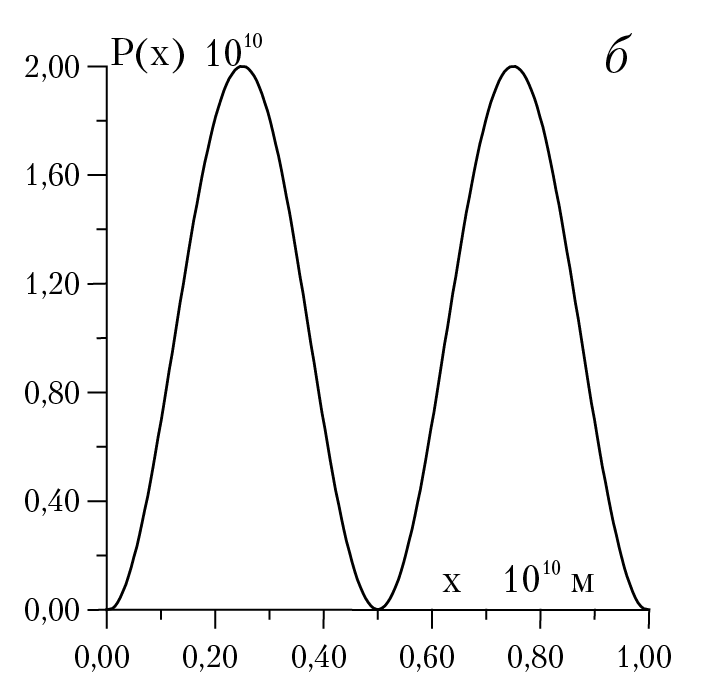
Рис. 1.3. Плотность вероятности обнаружения частицы a) n = 1; б) n = 2

1.6.3. Орбитальное и магнитное квантовые числа

Орбитальное квантовое число. Не только при движении частицы по прямой в ограниченном пространстве проявляются квантомеханические эффекты, но и при вращении частицы. Вспомним один из постулатов теории строения атома по Н. Бору: орбитальный момент электрона при его движении вокруг ядра может принимать только фиксированные значения: L = m[v × r] = h × n (n = 1, 2, 3...). Н. Бор никак не объяснял, почему орбитальный момент ротатора (частицы, которая движется по круговой орбите) не имеет право принимать любые значения. В квантовой механике все получается естественным образом. Еще де Бройль отмечал, что волновые свой­ства частицы должны проявлять себя таким образом, что длина волны λ = h/p (p = mv) частицы должна укладываться целым числом раз в области пространства, где происходит движение. При движении по окружности радиусом r должно выполняться равенство: 2πr = lλ, l = 0, 1, 2... и с учетом соотношения де Бройля получаем: 2πr = l ħ/p; L = p × r = l ħ; ħ = h/2π; угловой момент частицы L квантован, а значит будет квантована и энергия частицы, связанная с ее движением по окружности: E = L2/2I = (l ħ)2/2I, l = 0, 1, 2… I — момент инерции частицы. Точное решение уравнения Э. Шредингера для ротатора дает значение углового момента

и значение энергии ротатора: E = l(l + 1)ħ2/2I; l = 0, 1, 2...

Квантовое число l, которое определяет величину углового момента частицы

и циклическую частоту вращения

называется орбитальным квантовым числом. Если l = 0, это означает, что отсутствует вращательная составляющая в движении частицы.

Магнитное квантовое число. Угловой момент частицы, по определению, векторная величина (L = m[v × r]; v — скорость частицы, r — радиус вектор частицы). Пусть его направление совпадает с вектором j, перпендикулярном плоскости вращения ротатора и это направление определяет направление оси OZ декартовой системы координат. Мы уже отмечали, что описание ротатора методами квантовой механики предсказывает, что модуль вектора углового момента |L| квантован, т. е. может принимать только определенные значения. Но еще более удивительным следствием квантомеханического анализа свойств ротатора является тот факт, что и проекция углового момента на направление OZ так же квантовано, т. е. вектор углового момента ротатора не может принимать произвольное положение в пространстве: Lz = mh, m = 0, ±1, ±2... ±l (рис. 1.4).

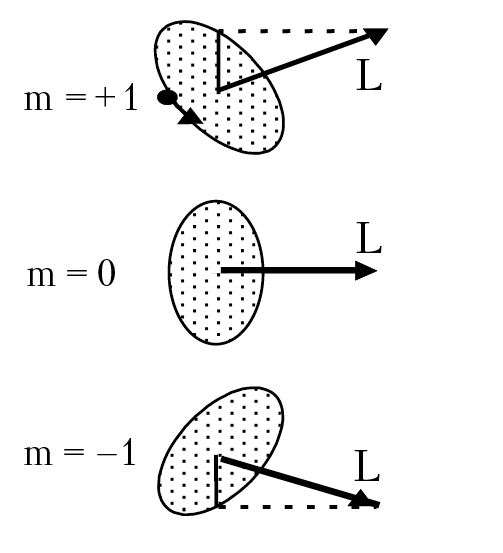
Рис. 1.4. Проекция орбитального момента на ось OZ

Квантовое число m, которое определяет направление оси вращения ротатора в пространстве, называется магнитным квантовым числом.

Магнитное квантовое число m также определяет значение проекции углового момента на выделенное направление и каждому значению m соответствует своя волновая функция частицы. Отметим, что в отсутствии внешнего воздействия на частицу энергия частицы зависит только от главного квантового числа n.

1.6.4. Спин электрона

Анализ тонкой структуры спектров излучения основных серий атомов щелочных металлов выявил дуплетное расщепление каждой линии. Например, желтая линия в спектре излучения натрия состоит из двух линий с λ1 = 5889,9Å и λ2 = 5895,9Å. Данный экспериментальный факт не имеет объяснения в рамках нерелятивистской квантовой механики Шредингера и Гейзенберга. В 1925 г. голландские физики С. Гаудсмит и Дж. Уленбек выдвинули гипотезу о существовании у электрона собственного момента импульса и связанного с ним магнитного момента. Эта гипотеза прекрасно объясняет экспериментальные факты. Но возникает проблема: если отталкивается от понятий классической механики, надо предположить, что электрон следует рассматривать как протяженное тело, для которого имеет место вращение вокруг собственной оси (отсюда и пошло название собственного момента электрона — спин электрона). Но тогда получается, что для собственного момента электрона (экспериментальное значение) и классиче­ского радиуса электрона re = 2,8 × 10–15 м, линейная скорость точек на поверхности электрона будет превышать скорость света в вакууме. В настоящее время принято считать спин электрона внутренним неотъемлемым свойством электрона, т. е. характеристикой электрона являются его масса 9,1 × 10–31 кг, заряд е = –1,6 × 10–19 Кл, спин (s — спиновое квантовое число, s = 1/2) и магнитный момент,

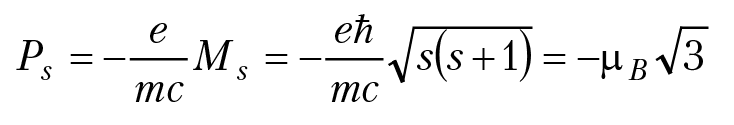
Следует отметить, что существование спина у электрона автоматически следует из релятивистского аналога квантовой механики П. Дирака, т. е. спин электрона является свойством одновременно квантовым и релятивистским. Таким образом, при анализе движения электрона в атоме мы должны принимать во внимание четвертое квантовое число s (спин электрона.)

1.6.5. Краткие итоги квантовой теории описания движения частицы

Отметим наиболее существенные моменты, которые надо принимать во внимание при описании движения частицы методами квантовой механики. Описание поведения частицы методами квантовой механики имеет смысл только в том случае, если размеры пространства, в котором движется частица, соизмеримы с длиной волны частицы в смысле де Бройля: L ≈ h/mv, L (м) — характерный размер пространства, в котором движется частица, mv — импульс частицы. Сам характер описания движения частицы принципиально отличается от классической трактовки движения частицы — отсут­ствует понятие о траектории движения частицы. И последнее — это квантовый характер движения частицы. Это означает, что основные характеристики частицы — положение в пространстве, энергия частицы, ее механический и магнитный моменты имеют право принимать строго фиксированные (квантованные) значения, пропорциональные квантовым числам. На примере атома водорода рассмотрим, как с помощью квантовой механики можно объяснить строение атомов.

1.7. Уравнение Э. Шредингера для атома водорода

Атом водорода — это система, состоящая из положительно заряженного ядра и электрона, который движется внутри ядра со скоростью порядка 105–107 м/сек. При анализе движения электрона в атоме необходимо принять во внимание корпускулярно-волновой характер движения электрона. Это означает, что надо записать уравнение Шредингера для электрона. В результате решения уравнения мы получим волновую функцию и значение энергии электрона в атоме. Уточним физический смысл волновой функции частицы φ(xyz) (Макс Борн, 1928). Выражение для волновой функции φ(x, y, z) частицы не отвечает привычному физическому образу, как например, смещению молекул воды при анализе волны на поверхности озера; физический смысл имеет квадрат волновой функции:

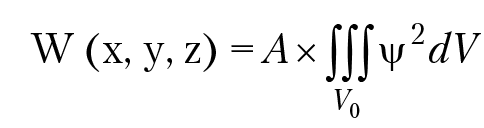
вероятность обнаружить частицу в точке пространства с координатами (x, y, z) в пределах объема V0. Физическая нтерпретация квадрата волновой функции налагает на нее требование однозначности в точке с координатами x, y, z и требование, что

если интегрирование распространяется на весь объем пространства, где можно обнаружить частицу (условие нормировки волновой функции и метод вычисления коэффициента пропорциональности А).

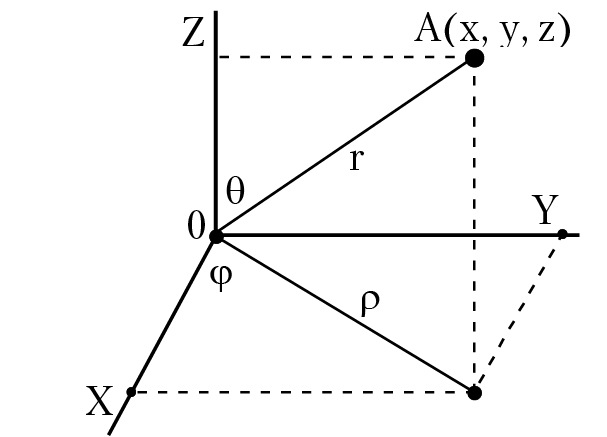
Рис. 1.5. Сферическая система координат

Для записи уравнения Шредингера необходимо зафиксировать систему координат, в начало которой поместим ядро; энергия взаимодействия электрона с ядром — это энергия электростатического взаимодействия заряженных частиц. В декартовой системе координат уравнение Шредингера имеет вид:

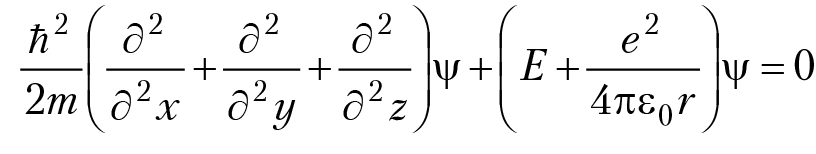
Ψ(x, y, z) — волновая функция электрона в декартовой системе координат.

Математический анализ уравнения Шредингера показал, что для его решения необходимо обеспечить разделение переменных (отметим, что если в уравнении Шредингера будет невозможно разделить переменные, тогда невозможно получить точное решение уравнения). Например, при решении уравнения Шредингера для атома гелия, лития и т. д. невозможно разделить переменные и, как следствие, невозможно получить точное решение уравнения. В нашем случае для разделения переменных надо перейти к сферической системе координат, рис. 1.5, а волновую функцию представить в виде произведения функций, которые зависят только от одной переменной:

Ψ(r, θ, φ)= R(r) × Θ(θ) × Ф(φ). В сферической системе координат уравнение Шредингера имеет вид:

(1.1)

Подставляя в уравнение Ψ(r, υ, φ), получим:

(1.2)

(1.3)

(1.4)

где B и m2 — постоянные разделения.

Решением уравнения (1.2 ) является функция R(r),

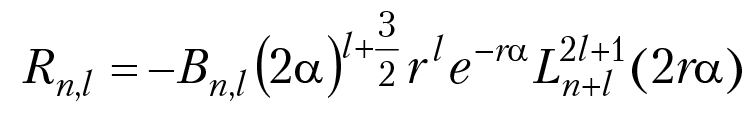
α = (n × a0)–1)

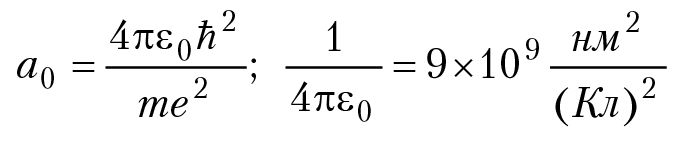(1.5)

где а0 = 0,529 Å (радиус Бора)

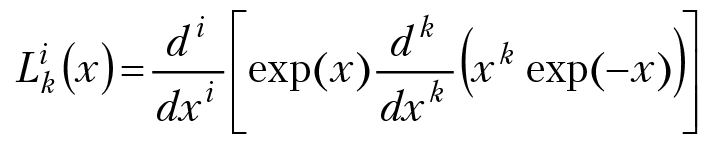
— полином Ляггера,

n = 0, 1, 2, 3..., l = 0, 1, 2, ..., n – 1.

Нормировочный множитель {В} найдем из условия

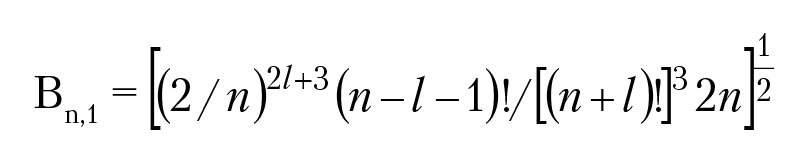
! — факториал числа.

Если

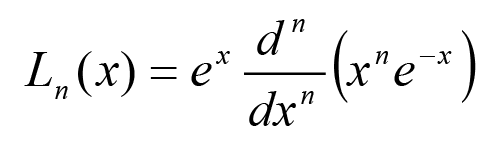
тогда L1(x) = 1 – x; L2(x) = 2 – 4x + x2; L3(x) = 6 – 18x + 9x2 – x3 и т. д.

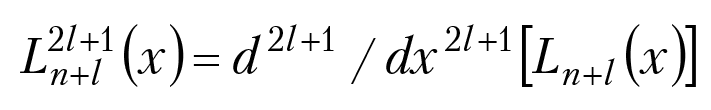
Для n = 1, l = 0 полином Ляггера (x) = L11(x)= – 1; n = 2, l = 0, L21(x) = – 4 + 2x; n = 2, l = 1, L33(x) = –6 и т. д.; x = 2(rα).

Решением уравнения (1.3) является функция Ф(φ) = exp(±imφ), m = 0, ±1, ±2, ±3.

Решением уравнения (1.4) является функция Θ(θ) (1.6)

Θ(θ) = Plm(cosθ), l = 0, 1, 2...; |m| ≤ 1 (1.6)

Plm(cosθ) присоединенный полином Лежандра. Аргумент полинома ограничен, так как –1≤ cos θ ≤ 1. Выпишем в явном виде выражения для полинома: х = cosθ; Р00 =1; Р10 = х; Р11 = – (1 – х2)1/2; Р20 = 1/2(3х2 – 1); Р21 = – 3х(1 – х2)1/2; и т. д.

Произведение Ylm(θ, φ) = А × Θ(θ) × Ф(φ) определяют как шаровая функция; Ylm — это угловая часть волновой функции Ψ(r,θ,φ). Нормировочный множитель А для шаровой функции Ylm равен:

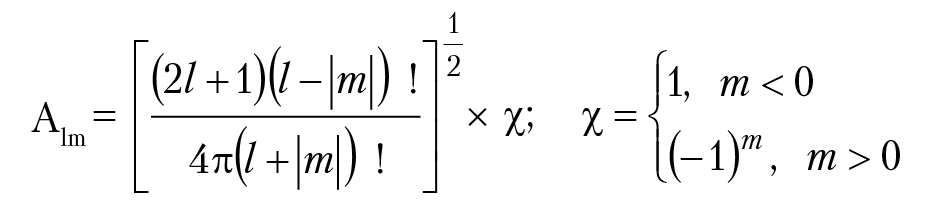
Ψ(r, θ, φ) = R(r) × Ylm(θ, φ) — волновая функция электрона в атоме водорода.

Энергия электрона в атоме водорода

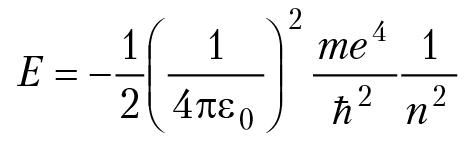
n = 0, 1, 2, 3...

Задача 1.2. Записать в явном виде волновую функцию электрона в основном состоянии атома водорода.

Решение: в основном состоянии квантовые числа электрона n = 1, l = 0, m = 0. Следовательно,

Rnl(r) = R10(r) = – B10(2α)0+3/2 r0 exp(–rα) L11(2rα); B10 = 2;

L11(2rα) = –1, R10(r) = (2α) 3/2 exp(–rα);

Ylm = A00P00(cos θ)e0 = π1/2;

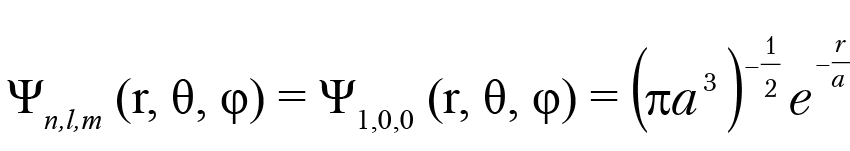
Таблица 1.1. Волновые функции электрона в атоме водорода

Отметим одно, чрезвычайно важное обстоятельство: решение уравнения Э. Шредингера (волновые функции электрона) зависят от трех целых чисел n, l и m, которые связаны между собой соотношениями: при заданном значении n, l = 0, 1, 2, 3, ... n – 1 и m = 0 ± 1... ± l. В таблице 1 приведены волновые функции электрона в атоме водорода для первых двух значений n. Аналитическая запись волновой функции Ψ (r, θ, φ) выражена через расстояние электрона до ядра r(Å) и сферические переменные θ и φ (рад) (рис. 1.5); a = 0,528 Å радиус первой боровской орбиты, n, l, m — квантовые числа. Индексы в обозначении волновой функции Ψnl определяют состояние электрона в атоме: 1s означает, что электрон находится в s-состоянии.

Задача 1.3. Вычислить среднее значение расстояния r электрона от ядра в основном состоянии атома водорода.

Решение: среднее значение переменной в квантовой механике вычисляется по формуле:

— оператор, соответ­ствующий переменной f, Ψ — волновая функция системы.

В нашем случае = r, Ψ = Ψ100, dV = sinθdθdφ r2dr.

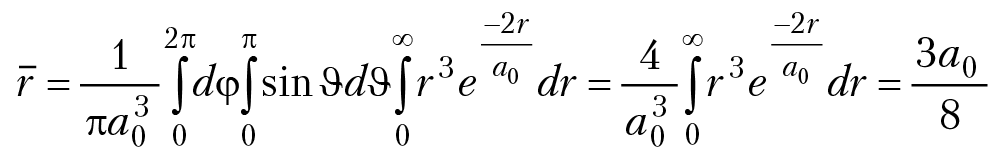
так как

a0 = 0,527 Å радиус Н. Бора.

Задача 1.4. Вычислить наиболее вероятное расстояние электрона от ядра в основном состоянии атома водорода.

Решение: вероятность нахождения электрона в элементе объема dV равна: dW = Ψ × Ψ dV.

Ψ × Ψ = P(r, θ, φ) плотность вероятности.

В нашем случае P(r, θ, φ) = (πa30)–1exp(–2r/a0).

Вероятность нахождения электрона в элементе объема dV на расстоянии от r до r + dr получим, если проинтегрируем по углам:

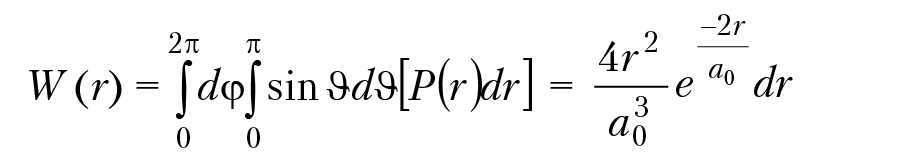
наиболее вероятное расстояние электрона от ядра найдем из условия, что

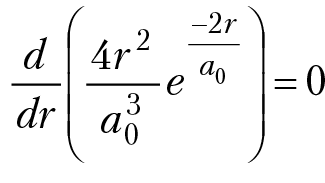
r = a0. Отметим, что среднее расстояние электрона от ядра равно 3/2 а0, наиболее вероятное расстояние электрона от ядра равно а0 = 0,529 Å.

1.7.1. Вырожденные состояния электрона в атоме

В результате решения уравнения Э. Шредингера для атома водорода мы получаем волновую функцию электрона и значение энергии электрона в атоме. Волновая функция электрона зависит от квантовых чисел и для каждого набора квантовых чисел n, l, m и s мы получаем соответствующую волновую функцию. А вот значение энергии свободного атома водорода, (в отсутствии внешних элек­трических и магнитных полей), зависит только от главного квантового числа n:

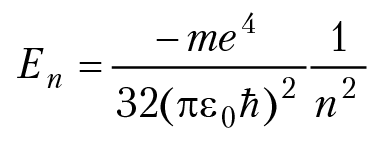
n = 1, 2, 3...

Если состояние электрона в атоме описывается разными волновыми функциями, но энергия электрона в этих состояниях одинаковая, говорят, что электрон находится в вырожденных состоя­ниях. Если атомы водорода поместить в сильное магнитное поле, возникает дополнительная потенциальная энергия взаимодействия электронов с внешним магнитным полем, в результате полная энергия атома водорода в магнитном поле будет завесить и от главного квантового числа n и от орбитального квантового числа l:

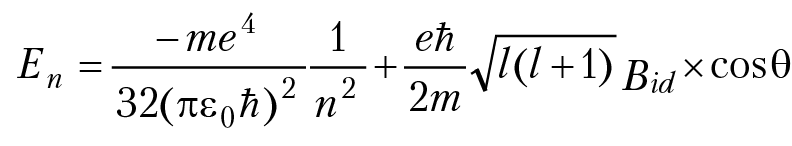
Bid — индукция внешнего магнитного поля, θ — угол между осью квантования орбитального момента электрона и направлением орбитального момента:

Так как во внешнем магнитном поле энергия атома зависит от орбитального квантового числа l, говорят, что снято вырождение по орбитальному моменту атома. Экспериментально это проявляется в возникновении дополнительных линий поглощения (испускания) в оптическом спектре атома, помещенном в сильное магнитное поле.

Отметим, что среднее значение расстояния электрона от ядра в случае снятия вырождения равно:

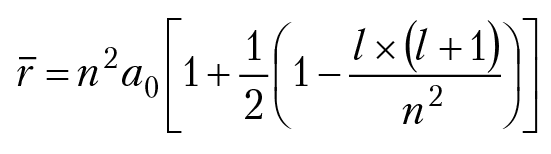
а0 = радиус Н. Бора.

1.7.2. Принцип заполнения атомных орбиталей

В 1920-е гг. ХХ столетия от рождества Христова полным ходом шло построение новой физической теории строения вещества. 1921 год. Опыты Штерна и Герлаха по исследованию тонкой структуры энергетических уровней атомов в сильных неоднородных магнитных полях. На основании этих опытов в 1925 г. Гаудсмит и Уленбек высказали гипотезу о существовании у электрона собственного механического и магнитного момента. Собственный момент электрона назвали спином электрона, а как было в последствии установлено на опыте, его значение:

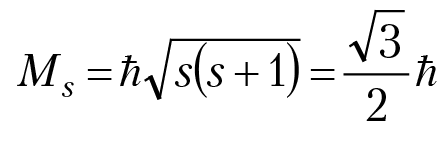
где s — спиновое квантовое число. Особенности устройства микромира постоянно напоминали о себе, непрерывно корректируя общепризнанные понятия. Так, с точки зрения классических понятий о равновесном состоянии системы, все электроны в атоме должны находиться в одном энергетическом состоянии с минимальной энергией, которая соответствует набору квантовых чисел: n = 1, l = 0, m = 0. Но опыт показывает, что кроме выполнения закона о минимальной энергии системы в стационарном состоянии, на состояние электронов в атоме накладываются дополнительные ограничения. На основании экспериментальных данных Паули высказывает гипотезу о том, что в любом квантовом состоянии (т. е. с определенным набором значений квантовых чисел n, l, m и s) может находиться только один электрон.

Принцип Паули, или принцип исключения: в одном и том же квантовом состоянии не может находиться более одного электрона.

Если один из электронов в атоме находится в квантовом состоя­нии с n = 1, l = 0, m = 0 и s = +1/2, то второй электрон не может находиться в этом же квантовом состоянии. Ближайшее по значению энергии квантовое состояние будет с n = 1, l = 0, m = 0 и s = –1/2. Принцип Паули справедлив не только для электронов, находящихся в одном и том же атоме, но и для всех электронов во Вселенной. При этом следует помнить, что состояния электронов различаются как по энергиям, так и по пространственному распределению. Отметим, что существуют микрочастицы, которые не подчиняются принципу Паули (световые кванты, мезоны и вообще все частицы с целым спином). При размещении электронов в атоме используют понятие слой электронов: при заданном значении главного квантового числа n = 1, 2, 3, 4, 5, 6, 7, l = 0, 1, 2, ... (n–1), m = 0 ± 1, ± 2, .., ± l, s = ±1/2. Отсюда получается, что число квантовых состояний, т. е. число электронов с данным значением n, равно 2 × n2. Все эти электроны образуют n-слой электронной оболочки атома.

Слой с n = 1 называется К-слоем и содержит 2 электрона. Слой с n = 2 называется L-слоем и содержит 8 электронов. Слой с n = 3 называется M-слоем и содержит 18 электронов, и т. д.

Кроме принципа Паули заполнения электронами вакантных мест в электронных оболочках атомов, необходимо придерживаться эмпирического правила Хунда: наименьшей энергией обладает электронное состояние с наибольшим возможным состоянием спина системы. Например, в атоме азота семь электронов, основное состояние атома можно записать как 1s2, 2s2, 2p3. Чтобы энергия атома в общем случае была минимальна, у трех электронов в 2р состояниях (это состояния 2px, 2py и 2pz которые соответствуют значениям m = 0, ±1) спины должны быть одинаково направлены и спиновое квантовое число s = 3/2 принимает максимальное значение.

1.7.3. Классификация состояний электронов в атоме.
(Классификация электронных состояний). Атомная орбиталь

Примечание. Многие понятия и названия в квантовой механике сохранились со времен «полуклассической» теории Н. Бора. С современной точки зрения эти понятия малоудачны, но широко используются по традиции. Например, далеко не однозначная аналогия между понятиями орбитального момента электрона в атоме и орбитальным моментом Земли при ее вращении вокруг Солнца.

Орбитальный момент частицы, с массой m, движущейся со скоростью u по окружности радиуса r равен m × [u × r]. Под орбиталь­ным моментом электрона понимают среднее значение оператора орбитального момента:

Если задано (или известно) состояние электрона в атоме, значит известны четыре квантовых числа n, l, m, s и волновая функция электрона. В этом случае говорят, что задана орбиталь электрона в атоме. В атомной физике принята следующая классификация электронных состо­яний:

• состояние электрона с l = 0 называют s-состоянием;

• состояние электрона с l = 1 называют p-состоянием;

• состояние электрона с l = 2 называют d-состоянием;

• состояние электрона с l = 3 называют f-состоянием, и т. д.

Вернемся к анализу орбитали электрона в атоме. Состояние электрона в атоме водорода задается квантовыми числами n, l, m и s, т. е. одновременно определяются четыре характеристики состояния электрона:

1) энергия, En = – R/n2, R = 13,6 эВ, n = 1, 2, 3, ...;

2) момент количества движения электрона в атоме:

l = 0, 1, 2, ... (n–1);

3) проекция Ml на ось квантования : Ml = hm, m = 0, ±1, ..., ±l;

4) собственный момент количества электрона (спин) ms = ±1/2ħ.

Местонахождение электрона в атоме определяют с помощью волновой функции электрона Ψn,l,m(r, θ, φ). Вероятность обнаружить электрон в окрестности точки с координатами [r, θ, φ] (см. рис. 1.5) в элементарном объеме dV = r2dr × sinθdθ × dυ = r2dr × dΩ равна: P(r, θ, φ)dV = |Ψn,l,m(r, θ, φ)|2dV = R2nl(r)r2dr × |Ylm(θ, φ)|2 dΩ. Первый сомножитель определяет вероятность нахождения электрона в шаровом слое толщиной от r до r + dr, второй сомножитель — вероятность найти электрон в пределах телесного угла dΩ.

Представляет большой интерес в теории строения атомов и молекул зависимость плотности вероятности нахождения электрона в атоме в зависимости от углов θ и φ; эта зависимость определяется функцией

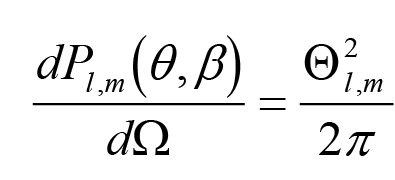
графики этой функции для l = 0, 1 и 2 приведены на рис. 1.6 Из анализа рисунка видно, что в s-состоянии наиболее вероятно найти электрон на поверхности сферы (см.решение задачи 1.3), не равна нулю вероятность обнаружить электрон внутри сферы и равна нулю вероятность обнаружить электрон за пределами сферы. Если n = 1, радиус сферы ≈ 0,529 Å.

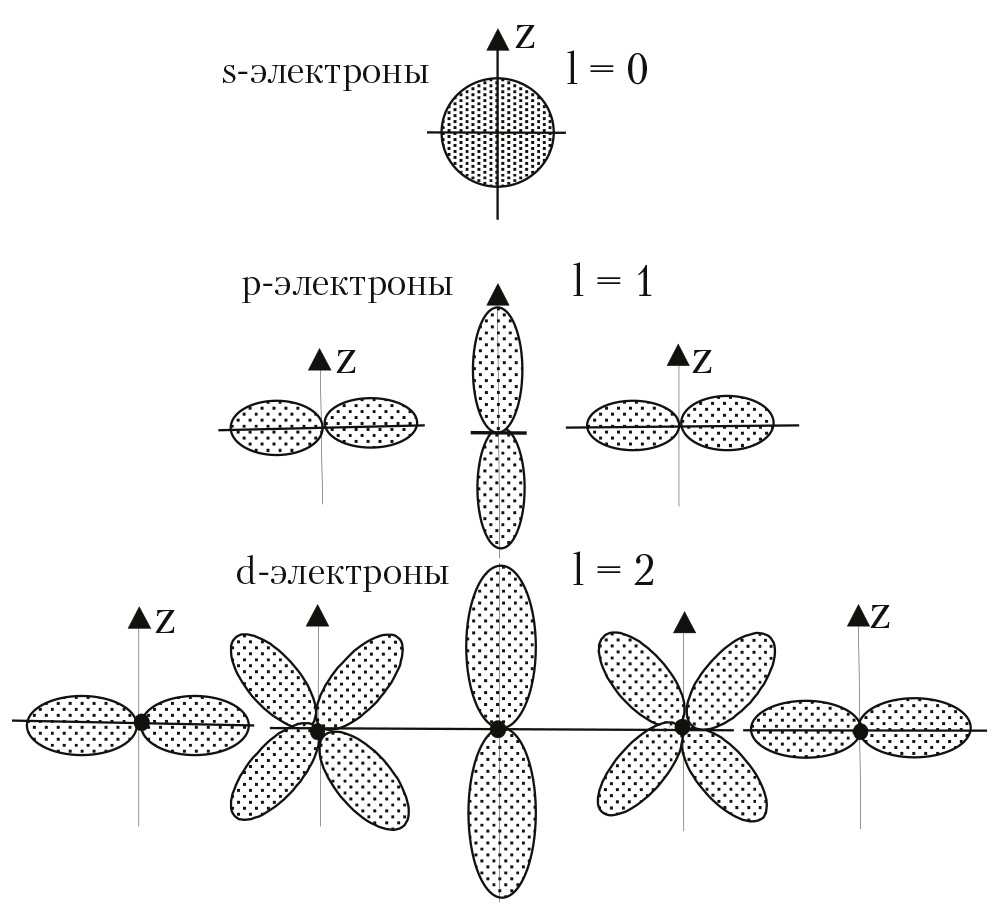
Рис. 1.6. Полярные диаграммы для s-, p-, d-состояний электрона в атоме

1.8. Периодическая система элементов Д. И. Менделеева

Теперь самое время установить связь между строением атома и его химическими свойствами. Как известно, в 1869 г. Д. И. Менделеев опубликовал периодический закон. Как писал сам Менделеев, периодический закон утверждает, что «свойства элементов, а следовательно, и образованных ими простых и сложных тел, находятся в периодической зависимости от атомных весов». Сегодня мы утверждаем, что периодичность свойств элементов обусловлена строением их электронных оболочек. Рассмотрим строение электронных оболочек атомов в невозбужденном состоянии.

Атом водорода. Z=1, n=1, l=0, m=0, s = 1/2. Эту информацию об электронном состоянии атома водорода можно записать в виде выражения: 1s1. В этом выражении цифра «1» — значение квантового числа n, показатель степени — число электронов в данном состоянии, символ «s» — состояние электрона с l = 0 (s-состояние электрона, следовательно l = 0).

Атом гелия. Не, Z = 2, n = 1, l=0, m=0, s=±Ѕ, 1s2.

Атом лития. Li, Z = 3, n = 2, 1s22s1 .

Атом бериллия. Be, Z = 4, n = 2, 1s22s2 .

Атом бора. B, Z = 5, n = 2, 1s22s22p1.

Атом углерода. C, Z = 6, n = 2, 1s22s22p2.

Атом азота. N, Z = 7, n = 2, 1s22s22p3.

Атом кислорода. О, Z = 8, n = 2, 1s22s22p4.

Атом фтора. F, Z = 9, n = 2, 1s22s22p5.

Атом неона. He, Z = 10, n = 2, 1s22s22p6.

Заполнение L-слоя закончено.

Атом натрия. Начало заполнения М-слоя. До калия продолжается «правильный порядок заполнения, п.п.з.». Причиной отступле­ния от п.п.з. — экранировка ядра атома внутренними электронами. Это приводит к относительному сдвигу энергии электронных орбиталей. Для s-электронов, с волновой функцией, имеющей сферическую симметрию электронного облака, экранировка ядра внутренними электронами наименее существенна, а для d- и f-электронов — значительное влияние. В атоме калия это приводит к тому, что вместо заполнения 3d-орбитали, электроны заполняют 4s-орбиталь:

Атом калия. K, Z=19, 1s22s22p63s23p63d4s1.

Атом кальция. Сa, Z=20, 1s22s22p63s23p63d04s2.

Начиная со скандия [Z=21] и до цинка [Z=30], элементы с порядковыми номерами 21–30 называются переходными элементами. На внешнем электронном слое этих элементов два 4s-электрона: 4s2. Особенность заполнения электронных оболочек этих элементов в том, что при переходе к каждому последующему элементу новый электрон размещается не во внешнем слое, а во втором внутри. А так как химические свойства элементов в первую очередь определяются структурой внешнего электронного слоя их атомов, то химические свойства переходных элементов изменяются незначительно по мере увеличения порядкового номера.

Атом скандия. Sc, Z=21, 1s22s22p63s23p63d14s2

Атом титана. Ti, Z=22, 1s22s22p63s23p63d24s2

Атом ванадия. V, Z=23, 1s22s22p63s23p63d34s2

Мы так много «нагрузили» d-уровень, что пора вспомнить и о том, что «распаривание» электронов (максимальный спин системы!) приводит к понижению энергии системы, а значит к новой перестановке уровней электронной энергии. Начиная с хрома, уровень 3d занимает свое законное место относительно уровня 4s и электрон с уровня 4s в атоме хрома переходит на уровень 3d.

Атом хрома. Cr, Z = 24, 1s22s22p63s23p63d54s1.

Атом марганца. Mn, Z = 25, 1s22s22p63s23p63d54s2.

Атом железа. Fe, Z = 26, 1s22s22p63s23p63d64s2.

И так далее. Мы уже обратили внимание на тот факт, что иногда заполнение последующих электронных уровней начинается до того, как завершится заполнение предыдущих.

Клечковским было сформулировано правило заполнения АО: заполнение АО атомных орбиталий происходит в порядке увеличения суммы главного и орбитального квантовых чисел n+l. Для данного значения суммы n+l заполнение орбиталей идет от больших l и меньших n к меньшим l и большим n. Но всегда сохраняется неравенство: l < n –1.

Порядок заполнения: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d…

Отклонения и от правила Клечковского наблюдается для Cr(24), Cu(29), Mo(42), Pd(46), Ag(47), Gd(64), Au(79). Анализ периодической таблицы элементов Д.И. Менделеева показывает, что с увеличением порядкового номера электронное строение ато­мов химических элементов изменяется периодически. Периодичность электронного строения проявляется в том, что через определенное число элементов снова повторяются s-, p-, d-элементы с одинаковой конфигурацией валентных электронов. Периодичность электронных структур приводит к периодическому изменению ряда химических и физических свойств элементов: атомных радиусов, потенциалов ионизации, сродства к электрону и т. д.

1.9. Местонахождение электрона в атоме

Свойства атома зависят от количества электронов в атоме и от их месторасположения в атоме. Но как определить, где находятся электроны в атоме? Решение этого вопроса упирается в необходимость выяснения физического смысла волновой функции электрона.

Согласно Шредингеру, квадрат волновой функции определяет величину плотности электрического заряда. Очевидно, чем выше плотность электрического заряда в данной точке, тем выше вероятность обнаружить электрон в данной точке. М. Борн предложил интерпретировать φ2dv как вероятность нахождения электрона в заданном элементе объема. Для заданного состояния электрона (т. е. когда заданы значения квантовых чисел электрона) значение волновой функции получается как результат решения уравнения Э. Шредингера для данного состояния электрона в атоме. Если (x, y, z) — декартовы координаты электрона в атоме (т. е. координаты того элемента объема, где мы предполагаем находится электрон), то в сферической системе координат, связанных с декартовыми координатами соотношениями: x = r sinθ×sinφ , y = r sinθ × cosφ , z = rcosθ , квадрат волновой функции электрона имеет вид: Ψ2(r, θ, φ) = R2(r) ×Θ2(θ)×Φ2(φ).

Рис. 1.7. Полярные диаграммы для s- и р-электронов

Особый интерес представляет изучение распределения вероятности нахождения электрона в атоме по углам θ и φ . Легко видеть, что вероятность нахождения электрона от угла φ не зависит, т. е. электронное облако обладает симметрией тела вращения. Что касается распределения вероятности по углу θ, то, задавшись определенным расстоянием от ядра r, мы можем найти это распределение, вычисляя значение Ψ2. Результаты данных расчетов и соответствующие построения приведены на рис. 1.7 Анализ рис. 1.7 показывает, что s-электроны наиболее вероятно можно обнаружить на поверхности сферы, с меньшей вероятностью внутри сферы и эта вероятность равна нулю за пределами сферы, радиус которой зависит от главного квантового числа n. р-электроны — на поверхности и внутри гантели, ориентация которой относительно декартовой системы координат, определяется значением магнитного квантового числа m. Для d-электронов мы получаем пять, различным образом ориентированных, фигур (m = 0, ±1, ±2), внутри и на поверхности которых можно обнаружить электрон.

В заключение отметим, что о положении электрона в атоме можно говорить только с вероятностной точки зрения, которая, в свою очередь, определяется состоянием электрона в атоме.