Геофизика

1.4.1. Прямые и обратные задачи гравиразведки

1.4.2. Геологическая интерпретация данных гравиразведки

1.4.3. Области применения гравиразведки

* * *

В результате гравиметрической съемки рассчитывают аномалии силы тяжести в редукции Буге (см. 1.1.2), обусловленные плотностными неоднородностями среды, и ведут их геологическую интерпретацию. Интерпретация данных гравиразведки (как и других геофизических методов) основана на физико-математическом и геологическом моделировании, включающем анализ гравитационных аномалий с обязательным использованием априорной геолого-геофизической и петрофизической (плотностной) информации об изучаемом районе (см. Введение).

1.4.1. Прямые и обратные задачи гравиразведки

Основой теории интерпретации данных гравиразведки является решение прямых и обратных задач. Прямая задача гравиразведки состоит в определении элементов поля силы тяжести по заданному распределению его источников, когда известны форма, размеры, глубина залегания и величина эффективной плотности. Обратная задача гравиразведки ставит противоположную цель: нахождение параметров объекта (формы, размеров, глубины залегания, эффективной плотности) по известному распределению (на профиле или на площади) элементов силы тяжести.

Решение прямой задачи в общем виде. Аномалии силы тяжести, вызванные притяжением тел известной формы, размера и избыточной плотности, рассчитывают на основе закона всемирного тяготения (закона Ньютона).

Для этого притягивающее тело разбивают на элементарные массы (dm); рассчитывают аномалию такой точечной массы (Δg1), которая равна вертикальной составляющей силы (F1) ньютоновского притяжения этой массой массы, равной 1 г, находящейся в точке наблюдения А, т. е. берут составляющую силы притяжения по направлению действия силы тяжести Земли (g); наконец, используя принцип суперпозиции, определяют аномалию за счет притяжения всем телом (ΔgT) как сумму притяжений всех элементарных точечных масс, которыми можно представить аномалообразующее тело (рис. 1.5).

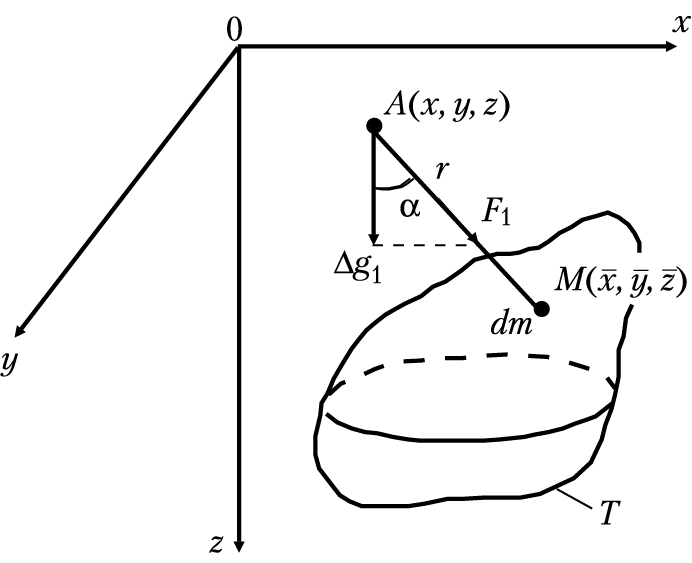
Рис. 1.5. Схема определения аномалий силы тяжести
от элементарной массы (dm) и гравитирующего тела (Т)

Математически это может быть выражено следующим образом. Согласно выражению (1.1):

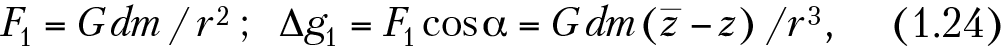
где

 —

расстояние между точкой наблюдения А (х, у, z) и точкой , в которой находится элементарная точечная масса (dm). В природных условиях аномальные включения с плотностью σ находятся во вмещающей среде с плотностью σ0, поэтому под массой dm надо понимать избыточную массу: dm = (σ — σ0)dV = ΔσdV, где dV — элементарный объем точечной массы; Δσ — эффективная плотность.

Окончательные выражения для расчета аномалии силы тяжести точечной массы и тела, используемые в теории гравиразведки, имеют вид

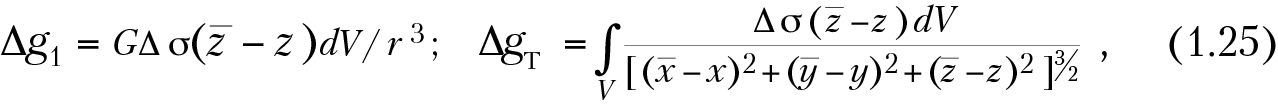
Интеграл в последней формуле берут по всему объему тела (V). При σ > σ0 значения ΔgT имеют положительный знак, т. е. наблюдаются увеличение притяжения и положительные аномалии. При σ < σ0 значения ΔgT имеют отрицательный знак, т. е. наблюдаются уменьшение притяжения и отрицательные аномалии.

Аналитические решения с помощью уравнения (1.25) получаются лишь для тел простой геометрической формы (шар, цилиндр и др.) с постоянным значением эффективной плотности. Для тел более сложной формы, особенно с переменной плотностью, возможны лишь численные решения интеграла (1.25) на основе сложных вычислительных схем. Анализ решений прямых задач служит основой при разработке приемов решения обратных задач гравиразведки для типовых геологических структур и объектов аналитическим методом.

Рассмотрим несколько примеров решения прямых и обратных задач для тел правильной геометрической формы.

Прямая и обратная задачи для шара. Пусть однородный шар радиусом R, объемом V, с избыточной плотностью Δσ расположен на оси Z на глубине h (рис. 1.6). Решим прямую задачу, т. е. определим гравитационный эффект вдоль наземного профиля ОХ, проходящего через проекцию центра шара с началом координат над ним. Поскольку по закону всемирного тяготения шар притягивается с такой же силой, что и точечная масса, сосредоточенная в его центре, аномалию над шаром (Δgш) можно получить без решения интеграла (1.25), считая, что аномалия силы тяжести над шаром и аномалия точечной массы, помещенной в его центре, совпадают:

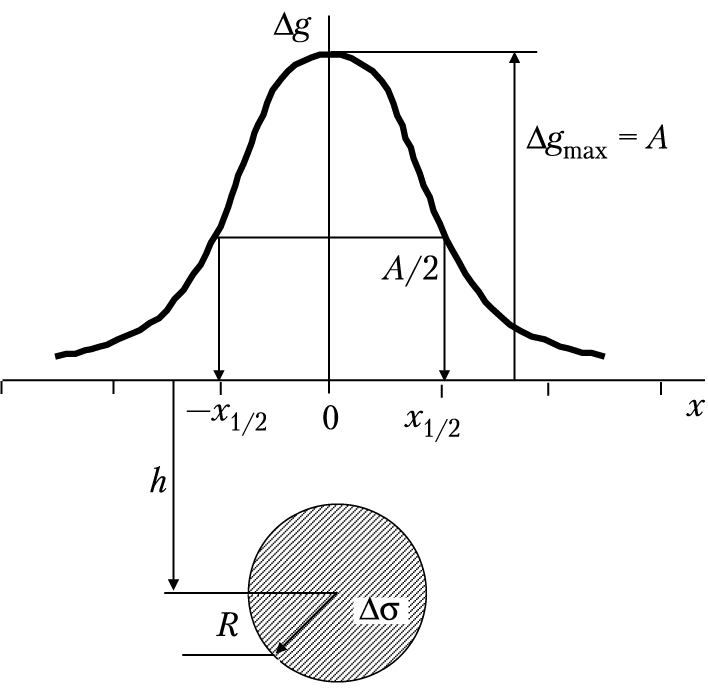
Рис. 1.6. Гравитационная аномалия (∆g(х)) от модели в виде шара
или горизонтального стержня (цилиндра) при Δσ > 0

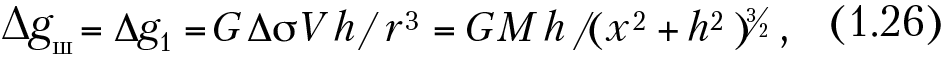
где M = ΔσV — эффективная масса шара.

График Δgш будет иметь максимум (при Δσ >0) над центром шара Δgmax(0) = GM/h2 = А и асимптотически стремиться к нулю при х → ± ∞ (см. рис. 1.6). Знак Δgш определяется знаком Δσ. Если провести расчеты по ряду профилей, то очевидно, что карта изолиний Δgш будет иметь вид концентрических окружностей с центром над шаром, т. е. аномалия Δgш в плане на плоскости х0у будет изометричной.

Из анализа уравнения (1.26) и графиков на рис. 1.6 можно решить обратную задачу. Например, найдем абсциссу x1/2, в которой Δgш достигает половины максимума:

откуда (x21/2 + h2)3/2 = 2h3. Решив это уравнение, получим:

|x1/2| = 0,76 h или h = 1,31 |x1/2|. (1.28)

Таким образом, определив по графику Δgш значения Δgmax, 1/2 ⋅ Δgmax и абсциссу точки кривой x1/2, где Δgш = 1/2 ⋅ Δgmax, и умножив ее на коэффициент 1,31, можно найти глубину залегания центра шарообразного объекта (h). Далее можно рассчитать эффективную массу (M = Δgmaxh2/G), а зная Δσ, определить радиус (R) или, зная R, получить значение ∆σ (табл. 1.2).

Таблица 1.2. Основные результаты решения прямой и обратной задач гравимагниторазведки

№ п/п	Модель объема	Формула расчета аномалии		Форма аномалии вдоль профиля 0Х		Характер аномалии на плоскости Х0Y		Амплитуда (σ0) аномалии (A)		Соотношение параметров аномалии и характеристик тела
		∆gа(х)	∆Zа(х)	∆gа(х)	∆Zа(х)	∆gа(х, у)	∆Zа(х, у)	∆gа(х)	∆Zа(х)	∆gа(х)	∆Zа(х)
1	Шар			один знак, один экстремум	два знака, три экстремума	изометричный	изометричный				IV =Ah3
2	Вертикальный стержень (цилиндр)	—		один знак, один экстремум	один знак, один экстремум	изометричный	изометричный	—		—	IS=Ah2
3	Горизонтальный стержень (цилиндр)			один знак, один экстремум	два знака, три экстремума	линейный	линейный				IS = Ah/2
4	Вертикальный пласт	—		один знак, один экстремум	один знак, один экстремум	линейный	линейный	—		—	I2bS = Ah/2

Примечание:  — абсцисса точки аномальной кривой, в которой значение функции равно нулю;

 — абсцисса точки аномальной кривой, в которой значение функции составляет половину амплитуды аномалии.

В геологической практике модель шара часто используется при аппроксимации интрузий батолитового типа, многих полиметаллических месторождений, карстовых образований и др.

Прямая и обратная задачи для горизонтального кругового цилиндра. Пусть горизонтальный бесконечно длинный круговой цилиндр радиуса R, сечения S, с избыточной плотностью ∆σ расположен вдоль оси у на глубине h (см. рис. 1.6).

Решим прямую задачу, т. е. определим ΔgГЦ вдоль оси х, направленной вкрест простирания цилиндра с началом координат над его центром. Притяжение цилиндра будет таким же, как притяжение вещественной линии, расположенной вдоль его оси с массой единицы длины dm = SΔσdy. Поэтому для точек наблюдения вдоль оси х (y = z = 0) с учетом того, что х = 0, –∞ < y < +∞ (цилиндр считается бесконечно длинным) и z = h, аналитическое выражение можно получить из уравнения (1.25):

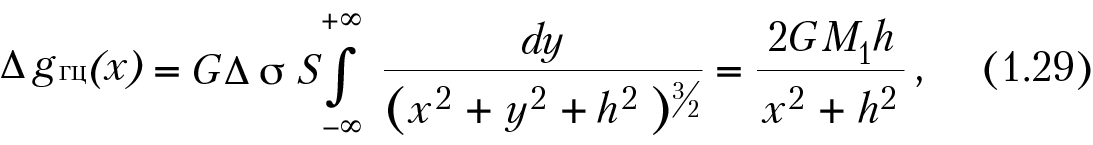
где М1 = SΔσ — эффективная масса единицы длины цилиндра.

График ΔgГЦ будет иметь максимум (при Δσ > 0) над центром структуры Δgmax(0) =  2GM1/h = А и, как и Δgш, асимптотически стремиться к нулю при х → ± ∞. В целом график ΔgГЦ вдоль оси х будет примерно таким же, как и над шаром. Очевидно, что в плане изолинии ΔgГЦ будут представлять систему параллельных оси цилиндра линий, т. е. аномалия ΔgГЦ в плоскости х0у будет линейной.

Решим обратную задачу для горизонтального бесконечно длинного кругового цилиндра тем же приемом, что и для шара:

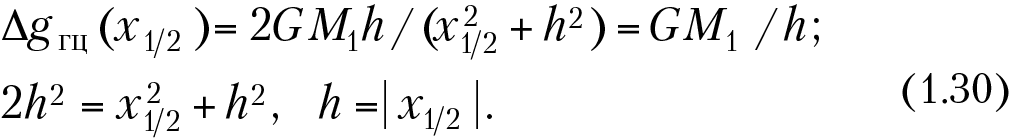
Таким образом, определив по графику ΔgГЦ значение Δgmax, 1/2 Δgmax и абсциссу x1/2, можно получить глубину залегания оси цилиндра (h) и далее рассчитать единичную эффективную массу (M1 = ∆σS = Δgmaxh/2G), а зная Δσ, можно определить площадь поперечного сечения цилиндра (S = πR2 = M1/Δσ) или его радиус (R), или, зная R, рассчитать ∆σ (см. табл. 1.2).

В реальных условиях модель горизонтального цилиндра применяется при аппроксимации валообразных поднятий фундамента, протяженных складчатых структур осадочного чехла, техногенных образований и пр.

Прямая и обратная задачи для вертикального уступа. Под вертикальным уступом в теории интерпретации гравитационных аномалий понимают горизонтальный полупласт, ограниченный вертикальной гранью, бесконечно простирающийся по оси y в какую-либо сторону от начала координат (рис. 1.7). Плотность пород уступа и вмещающих пород различна и составляет постоянную и отличную от нуля величину Δσ. Если глубину верхней горизонтальной плоскости, ограничивающей полупласт, обозначить h1, нижней — h2, а боковую вертикальную грань совместить с осью Z, то гравитационное поле Δgуст в точках x (вдоль оси х при z = 0 и y = 0) соответствует выражению (1.25) при определенных пределах интегрирования и может быть выражено аналитически:

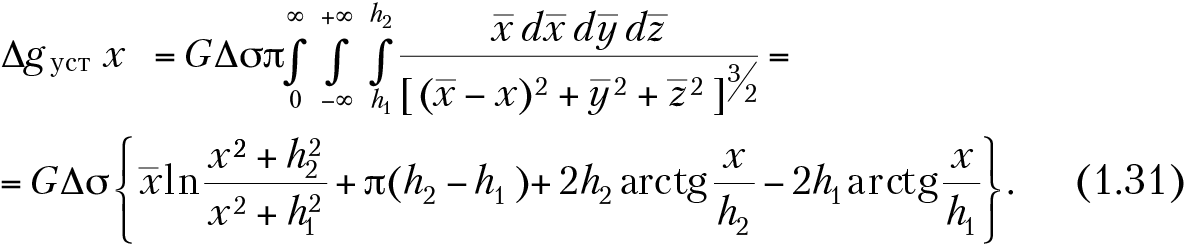
Вид кривой Δgуст (при σ > σ0) приведен на рис. 1.7. При х → ±∞ значения Δg выходят на горизонтальные асимптоты с максимальной амплитудой Δgmax = 2πGΔσΔh. Над самим вертикальным сбросом (при х = 0) получаем Δg = 1/2 ⋅ Δgmax = πGΔσΔh. Очевидно, на карте Δgуст будут наблюдаться параллельные изолинии с максимальным сгущением изолиний над вертикальной гранью. Из выражения (1.31) можно получить для абсцисс точек с x1/4 и x3/4, в которых Δgуст составляет 1/4 и 3/4 от Δgmax, выражение для определения средней глубины залегания вертикального уступа:

hср = (h1 + h2)/2 = x1/4 = x3/4. (1.32)

Если известна избыточная плотность (Δσ), то можно определить мощность вертикального уступа ∆h = Δgmax/2πGΔσ и рассчитать глубину залегания верхней (h1 = hcp – Δh/2) и нижней (h2 = hcp + Δh/2) кромок. Зная ∆h, можно рассчитать величину ∆σ.

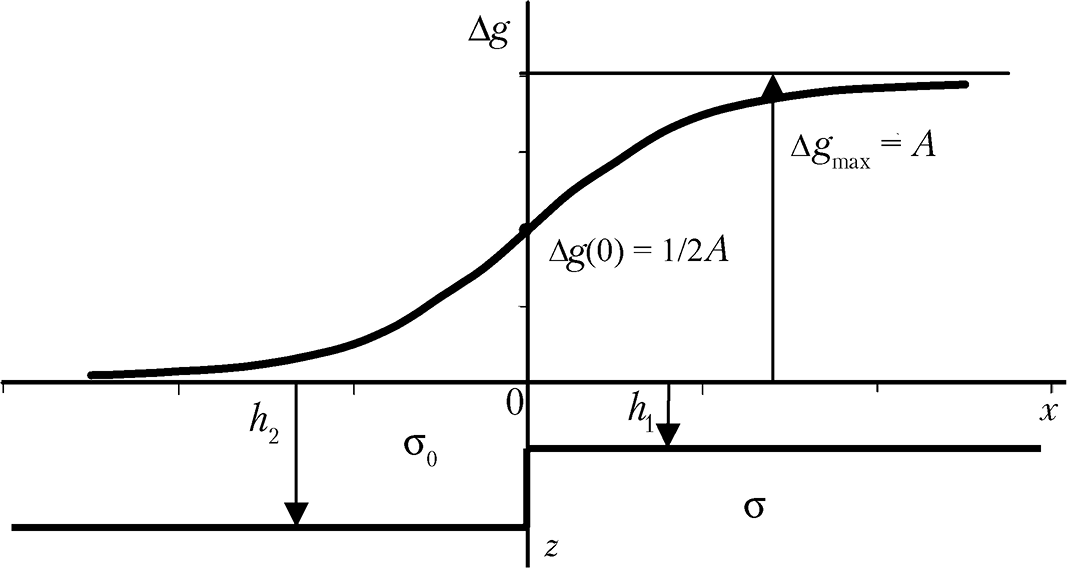
Рис. 1.7. Аномалия силы тяжести «гравитационная ступень»
от модели плотностной неоднородности в виде вертикального уступа

Моделью вертикального уступа часто аппроксимируют геологические объекты в виде сброса, участков вертикальных разломов, резких флексур и др.

Численные методы решения прямых задач гравиразведки. Для более сложных форм аномальных объектов с изменяющейся избыточной плотностью при решении прямой задачи гравиразведки применяют численные методы решения прямых задач гравиразведки. Для этого по заданному распределению масс получают значения элементов гравитационного поля, например, с помощью способов механических кубатур. Суть такого подхода — в замене реального объекта суммой (n) объектов простой геометрической формы и постоянной плотности. Гравитационный эффект (Δgi) от каждого i-го элементарного объема рассчитывают исходя из его элементарной формы, например по формуле (1.26) или (1.29), а значение Δg(x) в каждой точке определяют как их сумму:

Метод требует разбиения объекта на достаточно большое число ячеек, использования сложных, но повторяющихся в расчетах специфических выражений и поэтому относительно просто реализуется с помощью современных ЭВМ. Погрешность численного метода решения составляет 1–5 % в зависимости от формы элементарных объемов, их количества и степени аппроксимации.

Основные выводы из анализа решений прямых и обратных задач гравиразведки. Анализ решения прямых и обратных задач гравиразведки позволяет сделать следующие выводы.

1. В принципе прямая задача гравиразведки решается однозначно и от плотностной неоднородности существует единственная кривая аномалий силы тяжести. Точность получения данной кривой зависит от метода решения прямой задачи гравиразведки и степени аппроксимации данного объекта и закона изменения плотности плотностной неоднородности.

2. Обратная задача гравиразведки относится к классу математически некорректных и неоднозначных задач, т. е. одна и та же кривая аномалии силы тяжести может соответствовать нескольким плотностным неоднородностям разной формы (шар, куб и др.) и с разными геометрическими и плотностными параметрами.

3. Знак аномалии (Δg) определяется знаком эффективной плотности и над относительно «легкими» (Δσ < 0) объектами фиксируются отрицательные аномалии, а над более плотными (Δσ > 0) — положительные.

4. Экстремальные значения Δg наблюдаются над центрами тяжести этих объектов, а их амплитуды прямо пропорциональны избыточной плотности и обратно пропорциональны для вытянутых тел глубине, а для изометричных тел — квадрату глубины.

5. Форма аномалий Буге (ΔgБ) на картах и графиках тесно связана с пространственным положением эффективных масс: под вытянутыми (двумерными) аномалиями залегают вытянутые структуры или геологические тела, под изометричными — округлые в плане плотностные неоднородности.

6. Существует аналитическая или статистическая связь между абсциссами характерных точек на кривых ΔgБ и параметрами гравитирующих тел, что позволяет, аппроксимируя их телами простых геометрических форм, решать обратную задачу гравиразведки. При этом некоторые параметры, например h, рассчитывают достаточно однозначно. Для определения других параметров, например V, S, требуется привлечение дополнительных данных (эффективной плотности).

7. Чем глубже залегает тот или иной гравитирующий объект, тем более широкую и расплывчатую (региональную) аномалию создает он на земной поверхности (эффект дальнодействия).

1.4.2. Геологическая интерпретация данных гравиразведки

В практике геологической интерпретации результатов гравиразведки (карт или графиков ΔgБ) различают две стадии анализа — качественную и количественную.

Качественная интерпретация. Первым этапом интерпретации результатов гравиразведки (а в некоторых сложных условиях и при отсутствии сведений о плотности пород разреза — единственным) является качественная интерпретация. При качественной интерпретации дают визуальное описание характера аномалий силы тяжести по картам и профилям. При этом отмечают форму аномалий, их простирание, примерные размеры, амплитуду. Устанавливают связь гравитационных аномалий с геологическим строением, выделяют региональные аномалии, связанные со строением земной коры, региональными структурами и тектоническими зонами, и локальные аномалии, часто представляющие большой разведочный интерес, так как они связаны со строением осадочной толщи и указывают на местоположение отдельных структур, месторождений полезных ископаемых. Выделение региональных аномалий (плавных изменений аномалий (Δg) на значительных расстояниях) проводят методом сглаживания и другими. Вычитание региональных аномалий из наблюденного поля (снятие регионального фона) позволяет выявить локальные аномалии гравитационного поля (см. рис. 1.2).

Наблюденные аномалии гравитационного поля являются, как правило, сложными интерференционными полями. Они представляют собой сумму гравитационных эффектов от ряда геоструктурных этажей и геологических тел с различными законами распределения плотности, формой и глубиной залегания. В этих условиях не всегда удается визуально установить аномалию в «чистом» виде, не осложненную соседними аномалиями. Поэтому разработаны различные методы преобразований, или трансформаций исходного (наблюденного) аномального поля, которые «обостряют» (выявляют в визуально четкой форме) либо региональные, либо локальные аномалии. Наиболее распространены аналитические продолжения наблюденного поля в верхнее и нижнее полупространства, позволяющие выделить те или иные составляющие гравитационного поля. Пересчеты вверх, т. е. на уровни выше поверхности наблюдений, приводят к резкому уменьшению амплитуд локальных аномалий и несущественному изменению региональных. Это позволяет при оптимально выбранной высоте пересчета отождествлять трансформированные аномалии с региональным фоном. Пересчет наблюденного поля вниз, ниже плоскости наблюдений, так же как и вычисление высших производных поля силы тяжести, приводит к подчеркиванию локальных аномалий поля. Необходимо отметить, что при любом преобразовании наблюденного поля общее количество информации об источниках поля не возрастает, а, скорее, теряется, хотя делается она более наглядной. По картам и графикам Δgнабл или Δgлок и Δgрег, пользуясь выводами из решений прямых задач гравиразведки, можно сделать качественные заключения о плотностных неоднородностях, создающих эти аномалии. Например, определить местоположение центров возмущающих масс, простирание и форму аномальных тел, а по интенсивности аномалий судить об эффективной массе и глубине их залегания. Положительные аномалии соответствуют местоположению более плотных пород по сравнению с вмещающими, отрицательные — менее плотных или поднятию и опусканию какой-либо субгоризонтальной границы, на которой существует скачок плотностей горных пород. Зоны повышенных горизонтальных градиентов соответствуют крутым контактам пород разной плотности.

Количественная (расчетная) интерпретация данных гравиразведки основана на решении обратных задач и сводится к уточнению местоположения и количественной оценке глубины залегания центра тяжести, размеров, иногда эффективной плотности аномалообразующих масс. Решение обратной задачи неоднозначно, так как одинаковые аномалии силы тяжести могут быть созданы геологическими объектами разной формы, размеров и плотности. Тем не менее после проведения качественной интерпретации и изучения общего геолого-геофизического и плотностного строения района отдельные аномалии можно проинтерпретировать количественно с достаточной долей достоверности.

Существуют прямые методы количественной интерпретации, в которых элементы залегания гравитирующих масс определяют непосредственно по картам и графикам Δg, и косвенные приемы, основанные на сравнении наблюденных и теоретических кривых. При достаточно обоснованном предположении о форме объекта и уверенном выделении отдельных аномалий (Δg) применяют аналитический метод решения обратной задачи, при котором параметры плотностных неоднородностей определяют по характерным точкам кривой Δg. Такие соотношения для моделей простой геометрической формы в предположении постоянства избыточной плотности получены выше (см. выражения (1.28), (1.30), (1.32), табл. 1.2). Имеются аналогичные подходы и формулы расчета глубин для других тел простой геометрической формы. Погрешность количественного определения глубин даже по нескольким характерным точкам кривой Δg (x1/2, x1/4, x3/4 и т. д.) невелика и составляет в благоприятных условиях ±(20–30) %.

В теории гравиразведки разработаны также палеточные приемы интерпретации, с помощью которых всю наблюденную кривую Δg сравнивают с заранее рассчитанными теоретическими (палеточными) кривыми (Δgтеор) для моделей определенного класса и различных параметров. Задача количественной интерпретации в этом случае заключается в отыскании такой теоретической кривой (Δgтеор), которая наилучшим способом совпадает (или приближается) с наблюденной, и тогда параметры модели переносят на параметры объекта. Этот процесс автоматизирован и решается с помощью соответству­ющих программ на ЭВМ.

При сложном интерференционном характере аномального поля для решения обратной задачи гравиразведки применяют метод подбора. Суть этого метода состоит в последовательном переборе различных моделей плотностного строения разреза (I, II и т. д. приближения к реальной ситуации), расчета с помощью ЭВМ прямого гравитационного эффекта от этих моделей с помощью тех или иных методов решения прямой задачи, сопоставлении полученных значений Δg от моделей разного приближения (Δgтеор I, Δgтеор II и т. д.) с наблюденным полем (Δgнабл). Процесс подбора и сопоставления проводят до тех пор, пока не будет найдена модель, которая описывала бы поле Δgтеор, наиболее полно приближенное к Δgнабл. И для реализации этого метода разработаны специальные автоматизированные комплексы вычислительных компьютерных программ, позволяющие при разных ограничениях на форму объектов или на величины эффективной плотности получать данные о плотностном строении весьма сложных геологических районов.

Геологическое истолкование данных гравиразведки. Важным этапом качественной и количественной интерпретации данных гравиразведки является геологическое истолкование, которое сводится к сопоставлению выделенных аномалий и соответствующих плотностных неоднородностей с определенной геологической информацией и данными о плотностных особенностях горных пород и руд изучаемого района. Такое сопоставление обычно проводят на эталонных участках, где есть данные и геологии, и геофизики. Затем полученные закономерности и выводы о геологической природе составляющих аномального гравитационного поля распространяют на весь район исследования.

1.4.3. Области применения гравиразведки

Гравиразведка находит широкое применение при глубинных исследованиях Земли, структурно-геологическом изучении земной коры, рекогносцировочно-поисковых работах, поиске и разведке различных полезных ископаемых (нефти, газа, рудных, нерудных), при инженерно-геологических изысканиях.

Условия эффективного применения гравиразведки. Необходимыми предпосылками при решении тех или иных прикладных геологических задач с помощью гравиразведки являются следующие.

1. Геометрические условия. Форма плотностной структуры должна быть отлична от модели плоскопараллельного горизонтального слоя. Этому способствует наблюда­емая в геологической действительности реальная концентрация плотностных масс в объемах, аппроксимирующихся такими моделями, как вертикальный или горизонтальный цилиндр, шар, параллелепипед, вертикальный или наклонный пласт и т. п.

2. Физические условия. Величина эффективной плотности должна быть отлична от нуля. Этому способствует наблюдаемое различие плотности у разных типов пород и руд. Осложняющим фактором служит совпадение плотности у различных горных пород, например, когда осадочные породы, залегающие на значительных глубинах, по плотности тождественны некоторым кристаллическим породам.

3. Технические условия. Превышение по крайней мере в три раза амплитуды аномалий силы тяжести над уровнем погрешности гравитационной съемки. С развитием и усовершенствованием гравитационной аппаратуры возможности гравиразведки несомненно будут расширяться.

4. Наличие дополнительной геолого-геофизической информации о строении района исследования, снижающей неоднозначность решения обратной задачи гравиразведки и повышающей достоверность и точность интерпретации аномалий силы тяжести. Как правило, гравиразведка выполняется в комплексе с другими геологическими, геохимическими и геофизическими методами исследования.

В качестве примеров возможности применения гравиразведки рассмотрим региональные и поисково-разведочные работы.

Региональные гравиметрические съемки суши и акваторий. Значительная часть континентов и акваторий морей и океанов исследована с помощью проведения общей региональной гравиметрической съемки в масштабах мельче 1 : 200 000. Основными задачами региональной съемки являются: изучение литосферы и земной коры; оценка их мощности и строения; тектоническое районирование; выявление крупных структур; изучение строения фундамента; выявление перспективных площадей для поиска полезных ископаемых.

Интерпретация карт аномалий в редукции Буге (ΔgБ) качественная, а при наличии опорных геолого-геофизических профилей (как правило, сейсмических) может быть и количественной. На рисунке 1.8 приведен пример использования гравиразведки при решении региональной задачи по определению строения переходной зоны в районе Охотского моря. В результате интерпретации аномалий Буге выделены плотностные блоки с различной эффективной плотностью, соответствующие участкам океанической литосферы, покровно-мантийным комплексам литосферы переходного типа и областям относительно приподнятой астеносферы.

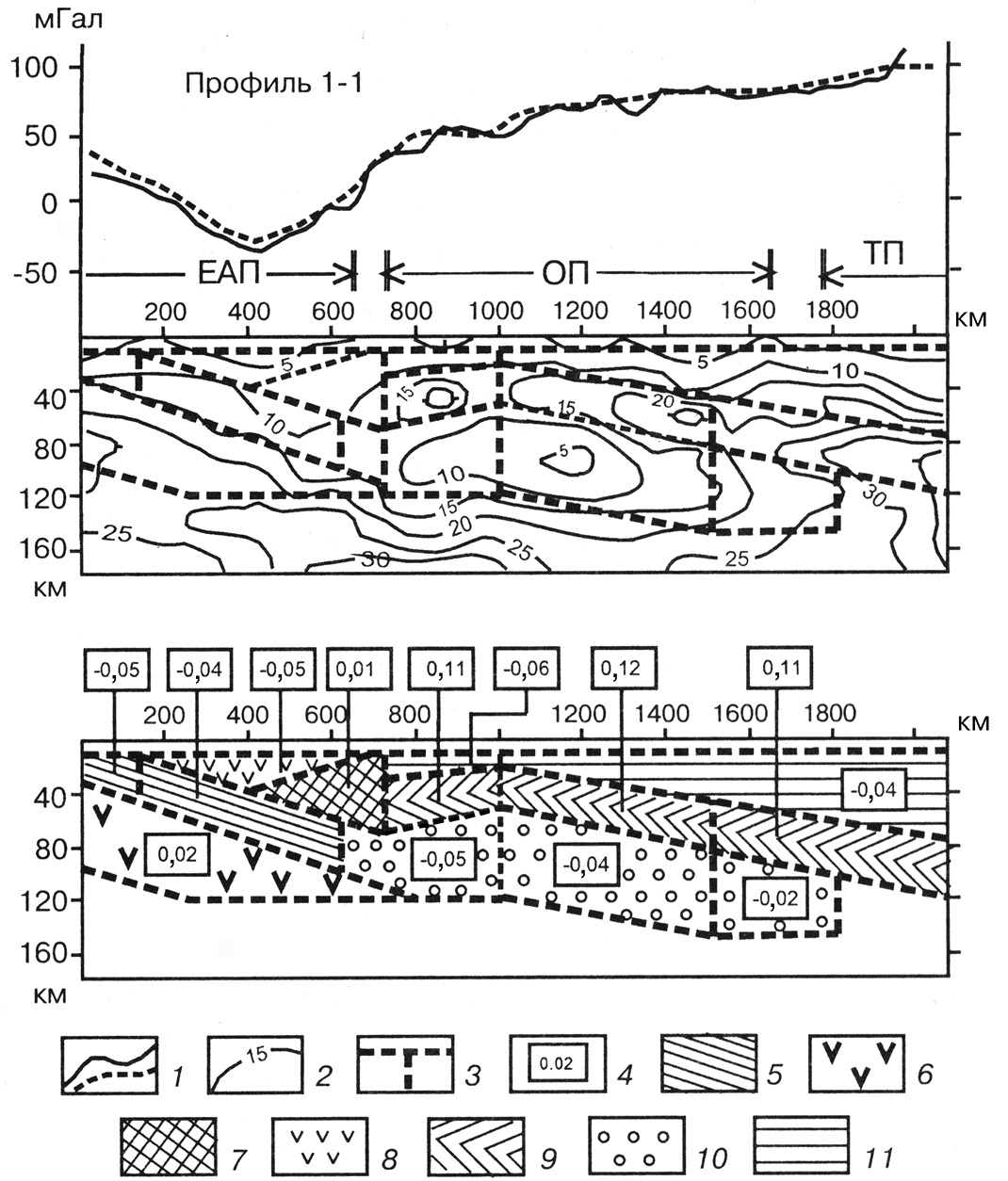
Рис. 1.8. Плотностная модель тектоносферы Охотского моря:

1 — наблюденный (сплошная линия) и расчетный (пунктирная) графики аномалий Буге
в условном уровне; 2 — изолинии μz (10–2 кг/м2/км); 3 — границы плотностных блоков;
4 — расчетная эффективная плотность блоков (10–3 кг/м3); 5 — континентальная земная кора;
6 — нижний слой континентальной литосферы; 7 — аккреционная призма;
8 — Охотско-Чукотский вулканический пояс; 9 — океаническая литосфера; 10 — астеносфера;
11 — покровно-мантийные комплексы литосферы переходного типа (А. М. Петрищевский, 2005)

В результате гравиметрических и сейсмических исследований обширных территорий континентов и океанов выявили прямую зависимость между мощностью земной коры и региональными аномалиями ΔgБ. Установлено, что в геосинклинальных областях отмечаются интенсивные (до –400 мГал) отрицательные аномалии, платформы характеризуются небольшими аномалиями разного знака, а на акваториях наблюдаются интенсивные положительные (до 400 мГал) аномалии, причем тем большие, чем меньше мощность земной коры. Объясняется это тем, что подошва земной коры (граница Мохоровичича) отделяет породы разной плотности: 2,8–3,0 г/см3 сверху и 3,1–3,3 г/см3 снизу. Поэтому обычно кривая ΔgБ отражает форму границы Мохоровичича, т. е. мощность земной коры.

По гравиметрическим и сейсмическим данным установлено, что при средней мощности континентальной земной коры на платформах примерно 30 км, под горами (в геосинклиналях) она достигает 70 км, а в океанах уменьшается до 5 км. В целом поверхность Мохоровичича зеркально повторяет форму поверхности рельефа Земли, в частности, существуют корни гор. Этот факт объясняют гипотезой изостазии, сущность которой сводится к представлению литосферы и земной коры в виде отдельных блоков, «плава­ющих» в пластичном подкоровом веществе (верхней мантии). Подчиняясь закону Архимеда — чем больше нагружен блок (например, горами), тем глубже он погружается своей нижней частью, — блоки земной коры как бы «плавают» и избыток масс на поверхности компенсируется недостатком внизу.

По региональным гравиметрическим аномалиям типа гравитационной ступени выделяют глубинные разломы с вертикальными перемещениями соседних блоков. На платформах с большой мощностью осадков (свыше 2–3 км) кривая ΔgБ характеризует поведение кровли кристаллического фундамента: максимумам соответствуют поднятия в фундаменте, минимумам — прогибы. На участках небольшой глубины фундамента (до 2 км) кривая ΔgБ характеризует и литологический состав фундамента, и его рельеф.

При региональных гравиметрических работах удается успешно решать различные задачи структурной геологии, выделяя по соответствующим аномалиям Буге различные структуры земной коры, отличающиеся от вмещающих пород по плотности. Так, в пределах Якутии гравиразведка помогла выявить форму и определить глубину заложения структуры Сарычева (рис. 1.9).

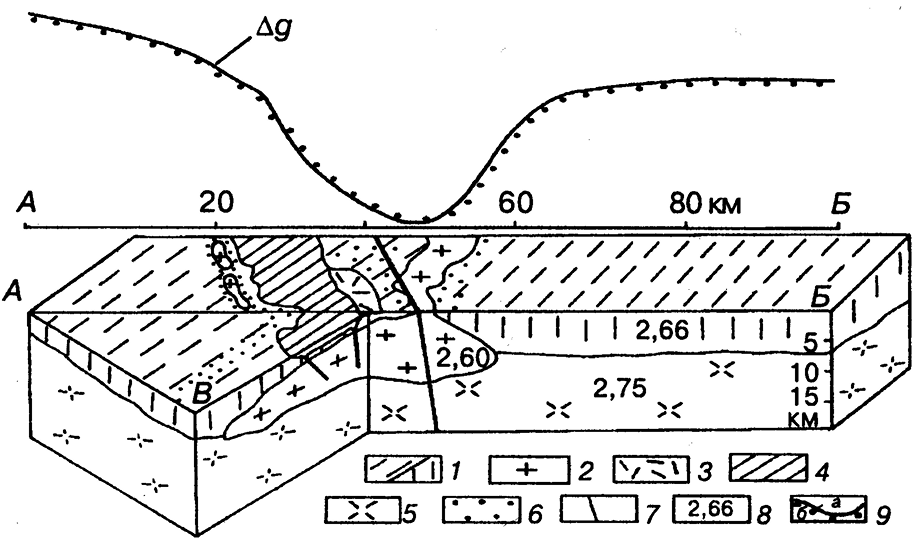
Рис. 1.9. Модель глубинного строения структуры Сарычева (Якутия):

1 — осадочные отложения; 2 — граниты; 3 — вулканиты; 4 — дациты; 5 — метаморфические породы;
6 — зоны метаморфизованных пород; 7 — тектонические нарушения; 8 — значения плотности (г/см3);
9 — кривая силы тяжести в редукции Буге (А — наблюденная, Б — расчетная)
(В. В. Стогний, Г. А Стогний., С. П. Васильев, 2000)

Поиски и разведка полезных ископаемых. Важным направлением гравиразведки являются поиски и разведка нефтегазовых структур: соляных куполов, антиклинальных складок, рифовых массивов, куполовидных платформенных структур. Наиболее благоприятны для разведки соляные купола, поскольку соль отличается низкой плотностью (σ = 2,1 г/см3) по сравнению с окружающими породами и резкими крутыми склонами. Соляные купола, находящиеся в Урало-Эмбенском районе, Днепровско-Донецкой впадине и других районах, выделяются изометрическими интенсивными отрицательными аномалиями, по которым можно судить не только об их местоположении и форме, но и о глубине залегания.

Антиклинальные складки выделяются вытянутыми изолиниями аномалий (ΔgБ) положительного и отрицательного знака в зависимости от плотности пород, залегающих в ядре складок. Интерпретация результатов качественная, изредка количественная.

Многие месторождения нефти и газа приурочены к рифовым массивам, но их разведка гравиметрическим методом является задачей нелегкой. Для разведки рифовых известняков среди осадочных терригенных пород используют анализ как региональных, так и локальных аномалий, причем рифовые известняки выделяются, как правило, положительными аномалиями. Куполовидные платформенные поднятия, к которым также нередко приурочены месторождения нефти и газа, отличаются малой амплитудой и большой глубиной залегания. Применение высокоточных гравиметров позволяет вести разведку и этих структур, выделяющихся слабыми отрицательными аномалиями за счет разуплотнения пород над поднятиями.

В связи с разведкой угольных месторождений гравиметрию применяют как для определения границ угольного бассейна, так и для непосредственных поисков отдельных месторождений и пластов угля. В некоторых случаях мощные, неглубоко залегающие угольные пласты выделяются минимумами ΔgБ за счет малой (σ = 1,1 г/см3) плотности углей.

Гравиразведку применяют в комплексе с другими геофизическими методами также для разведки рудных и нерудных ископаемых, причем ее привлекают как для крупномасштабного картирования и выявления тектонических зон и структур, благоприятных для залегания тех или иных ископаемых, так и для непосредственных поисков и разведки месторождений. Существенное отличие рудной гравиметрии от нефтяной состоит в меньшей глубинности, большей детальности и точности разведки.

Классическим примером применения гравиметрии являются поиски и разведка железорудных месторождений (особенно Курская магнитная аномалия и Кривой Рог), где гравиразведку применяют для изучения структуры бассейна, картирования железорудной толщи и поисков богатых руд. На железорудных месторождениях наблюдаются локальные положительные аномалии за счет высокой плотности железосодержащих руд. Работы проводят совместно с магниторазведкой, что позволяет определить размеры, глубины залегания, мощности рудных залежей (подробнее см. главу 2). Из-за высокой плотности хромитов гравиразведка практически является единственным методом поисков и разведки хромитовых руд.

На рудных колчеданных и полиметаллических месторождениях гравиразведка существенно дополняет методы электроразведки при отделении рудных электрических аномалий от безрудных. С залежами колчеданных руд связаны интенсивные положительные аномалии за счет их повышенной плотности.

Широкое применение находит гравиметрия и при разведке нерудных ископаемых. Интенсивными положительными локальными аномалиями ΔgБ часто выделяются пегматитовые, кварцевые, корундовые, баритовые жилы, кимберлитовые алмазные трубки, месторождения слюд, марганца, боксита и многих других ископаемых. Минимумами ΔgБ выделяются месторождения минеральных солей.