* * *
1.1.1. Нормальное гравитационное поле Земли
Нормальное гравитационное поле представляет собой поле ускорений силы тяжести планеты Земля с усредненными характеристиками (нормальной Земли), без каких-либо плотностных неоднородностей, связанных с геологическими структурами литосферы.
Согласно закону всемирного тяготения все тела притягиваются друг к другу с силой, пропорциональной их массе и обратно пропорциональной квадрату расстояния между ними. Для точечных масс, т. е. для масс, сосредоточенных в бесконечно малом объеме, справедлив закон всемирного тяготения Ньютона:
где F — сила притяжения; m1, m2 — взаимодействующие массы; r — расстояние между их центрами; G — коэффициент пропорциональности, называемый гравитационной постоянной, в системе СИ G = 6,67 10–11 м3 кг–1 с–2.
Если силу притяжения отнести к единичной массе (т1 = 1), то точечная масса (т2 = m) будет притягивать ее с силой, равной ускорению силы притяжения :
В случае притяжения единичной массы телом, состоящим из отдельных точек (n) с массой (mi), ускорение силы притяжения принимает вид
При непрерывном распределении притягиваемых масс сумма заменяется интегралом по всему занимаемому массами объему (V):
В теории притяжения доказано, что однородное сферическое тело притягивает массу с силой, развиваемой точечной массой, сосредоточенной в его центре. Поэтому, представляя в первом приближении Землю в виде сферически однородного шара, получаем ускорение силы равным:
где М — масса Земли; r — средний радиус Земли, если притягиваемая точка А находится на ее поверхности (рис. 1.1).
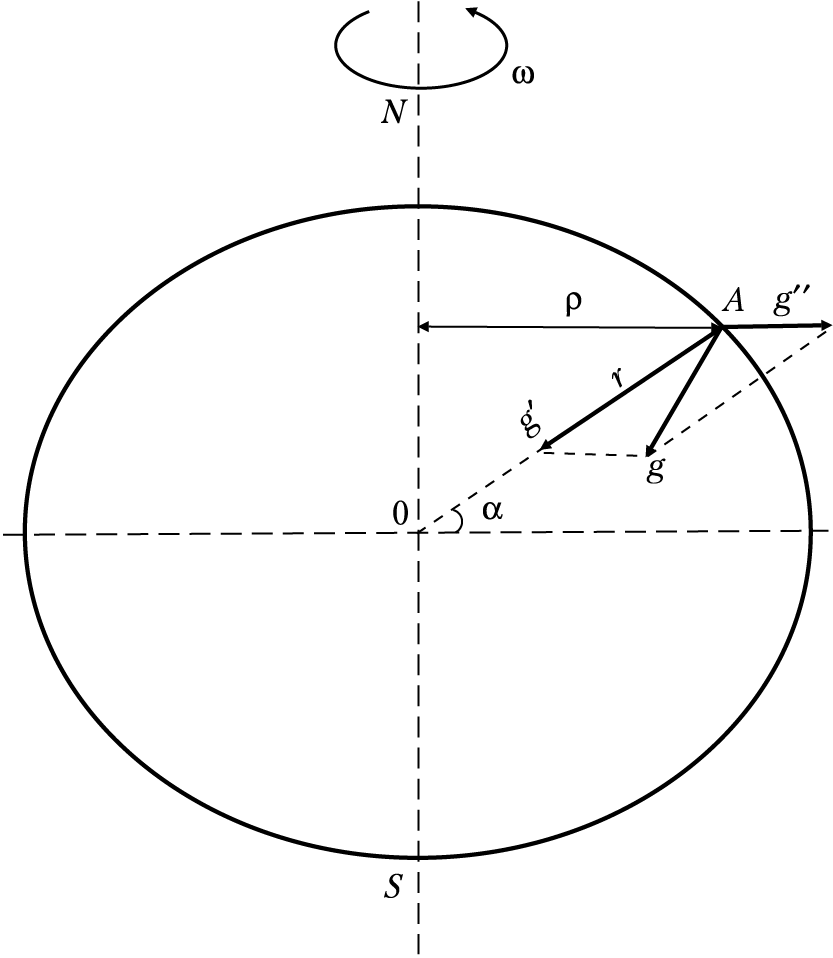
Рис. 1.1. Нормальное поле силы тяжести и составляющие силы тяжести:
g′ – ускорение силы притяжения; g″ — ускорение центробежной силы; g — ускорение силы тяжести;
r — радиус Земли в точке А, равный в случае шара R; ρ — радиус вращения точки А; α — широтный угол
Кроме силы притяжения на массу (т) действует центробежная сила, возникающая вследствие суточного вращения Земли вокруг своей оси. Эта сила пропорциональна радиусу вращения (ρ) и квадрату угловой скорости (ω):
Относя ее к единичной массе, получаем ускорение центробежной силы g′′, направленное по радиусу вращения от оси вращения:
В общем случае нормальное гравитационное поле (γ0) Земли в виде шара представляет собой равнодействующую ускорений притяжения (g′) и центробежной силы (g′′):
γ0 = g = g′ + g′′. (1.8)
Отношение максимального значения ускорения центробежной силы (на экваторе) к минимальному значению ускорения притяжения (на экваторе) составляет 1/288, т. е. основной вклад в структуру гравитационного поля Земли вносит ускорение притяжения, поэтому во многих случаях можно считать g ≅ g′.
Единицей ускорения свободного падения в системе СИ является метр на секунду в квадрате. В гравиразведке используют более мелкую единицу: 1 мГал = 10–5 м/c2 = 10–3 cм/c2, которая получила свое название в честь знаменитого итальянского ученого Галилео Галилея. В настоящее время в связи с повышением точности измеряющей аппаратуры используются еще более мелкие единицы: 1 мкГал, равный 10–8 м/с2, и 1 нГал, равный 10–11 м/с2.
У поверхности Земли γ0 изменяется от 9,780 м/с2 на экваторе до 9,825 м/с2 на полюсах при среднем значении 9,810 м/с2. Наблюдаемое увеличение γ0 от экватора к полюсам объясняется, с одной стороны, изменением ускорения центробежной силы, а с другой — уменьшением радиуса Земли примерно на 21 км по оси вращения, т. е. сжатием Земли.
Если представить форму Земли в виде эллипсоида вращения малого сжатия (α = 298,26), нормальное значение ускорения силы тяжести (γ0) можно выразить, например, по Элкинсу, формулой
γ0 = gнорм = gэ(1 + 0,005302sin2φ – 0,000007sin22φ), (1.9)
где gэ — среднее значение поля на экваторе Земли; φ — широта наблюдения.
Это выражение позволяет рассчитать γ0 на поверхности геоида, т. е. уровенной поверхности однородной Земли, совпадающей с невозмущенной поверхностью океана. С ростом количества точек наблюдений и повышением точности самих измерений g численные коэффициенты и их количество в формуле (1.9) будут меняться, поэтому существует несколько вариантов аналитического расчета значений нормального гравитационного поля как для всей поверхности Земли, так и для территорий отдельных государств, что необходимо учитывать при анализе гравитационных данных сопряженных или пограничных территорий.
1.1.2. Аномалии и редукции силы тяжести
Реальная Земля отличается от «нормальной» прежде всего наличием плотностных неоднородностей литосферы, связанных с отклонением фактической плотности горных пород литосферы от среднего значения, принятого при расчете нормального поля, и отклонением поверхности Земли от невозмущенной поверхности океана (h = 0). Именно эти причины приводят к несовпадению наблюденного и нормального гравитационных полей в точке наблюдения.
Аномалией силы тяжести называют отклонение наблюденного значения (gнабл) от нормального поля, теоретически рассчитанного для этой же точки, например, по формуле
Δg = gнабл – γ0. (1.10)
Для соблюдения корректности этой операции необходимо, чтобы уровень (высота относительно уровня моря) и условия (в воздухе, на физической поверхности и т. д.) наблюдения соответствовали параметрам расчета нормального гравитационного поля. Поэтому в наблюденные значения силы тяжести вводят поправки, или редукции, снимающие эти расхождения и приводящие наблюденные и теоретические значения к одной поверхности и к одним условиям. Существуют три основные редукции. Поправка за свободный воздух (за высоту, или поправка Фая) учитывает разницу в уровне наблюдения, т. е. высоту над геодом, и рассчитывается по формуле (в мГал)
Δgсв.возд = 0,3086h, (1.11)
где h — высота точки наблюдения над уровнем моря, выраженная в метрах.
Аномалией Фая (ΔgФ) называют аномалию силы тяжести, полученную с учетом различия высот точек наблюдения:
ΔgФ = gнабл – γ0 + Δgсв.возд. (1.12)
Поправку за свободный воздух вводят в gнабл со знаком плюс, если наблюдения проводят над уровнем моря, и со знаком минус, если наблюдения осуществляются ниже уровня моря. При погрешности относительных гравиметрических измерений ±0,01 мГал разница в высотах должна быть известна с погрешностью не более 4 см.
Аномалии Фая в основном используют в геодезической гравиметрии, а также при оценке геодинамического состояния земной коры и литосферы.
При наземных съемках на участках, приподнятых по отношению к уровню геоида, между поверхностью наблюдения и геоидом располагаются массы горных пород, которые при введении поправки за свободный воздух виртуально смещаются на величину h и «накладываются» на нижележащие массы, создавая как бы двойной плотностной эффект. Для исключения влияния масс, расположенных между поверхностью наблюдения и уровнем нормального поля, вводят поправку за промежуточный слой — поправку Буге (ΔgБ). Для выровненного спокойного рельефа поверхности наблюдения, когда массы промежуточного слоя можно представить в виде плоскопараллельного горизонтального слоя мощностью h (в м), эту поправку вычисляют по формуле (в мГал)
ΔgБ = –0,0418σh, (1.13)
где σ — средняя плотность пород промежуточного слоя в г/см3.
При расположении точки наблюдения выше уровня моря поправку ΔgБ вводят в наблюденные значения силы тяжести со знаком минус.
Если отклонения рельефа местности в районе наблюдения значительны (горные районы, переходные и рифтовые зоны и др.), то поправка за промежуточный слой должна учитывать влияние масс рельефа, окружающего точку наблюдения, т. е. масс, заключенных между уровенной поверхностью, проходящей через точку наблюдения (в ее ближайших окрестностях эта поверхность горизонтальна), и физической поверхностью. Массы рельефа, залегающие над этой горизонтальной поверхностью, создают вертикальную составляющую силы тяжести, направленную вверх, т. е. уменьшающую наблюденное значение. При опускании физической поверхности ниже горизонтальной создается недостаток масс рельефа (вместо горных пород нормальной плотности находится воздух), что также ведет к занижению наблюденных значений силы тяжести. Поэтому поправку за рельеф Δgр, которая рассчитывается по специальным формулам, всегда вводят в gнабл со знаком плюс.
Поправка Буге, или полная поправка за промежуточный слой, имеет вид
ΔgБ = –0,0418σh + ΔgР, (1.14)
В зависимости от точности наблюдений используют топографические карты различного масштаба, с помощью которых определяют влияние масс рельефа в области радиусом порядка 200 км и более от точки наблюдения. Причем для близко расположенных к точке наблюдения участков необходимы более точные карты рельефа местности.
Аномалия Буге (ΔgБ) представляет собой разность наблюденного и теоретического полей силы тяжести при введении соответствующих поправок:
ΔgБ = gнабл – γ0 + Δgсв.возд + ΔgБ, (1.15)
где γ0, Δgсв.возд, ΔgБ определяют по формулам (1.9), (1.11) и (1.14).
Обычно в качестве начального значения плотности промежуточного слоя при расчете аномалий Буге выбирают значение средней плотности горных пород земной коры, равное 2,67 г/см3. Для осадочных бассейнов эта величина может составлять 2,3 г/см3.
При высокоточных гравиметрических съемках необходимо вводить поправки за лунно-солнечные возмущения силы тяжести, связанные с различным расположением Солнца и Луны по отношению к точке наблюдения и достигающие 0,16 мГал.
Аномалии Буге практически каждой территории представлены набором аномалий от разноглубинных и разномасштабных плотностных неоднородностей, отражающих локальные и региональные составляющие (рис. 1.2). Такое разделение аномалий связано с их разной частотной характеристикой: более высокочастотные аномалии относятся к локальным, а более низкочастотные — к региональным. Для выявления локальных аномалий Буге (Δgлок) от, например, геологических структур осадочных бассейнов, отдельных интрузий, карстовых образований, рудных тел и других из наблюденного поля (Δgнабл) исключают региональную составляющую (Δgрег), вычисляемую различными математическими (статистическими и др.) способами. На рисунке 1.2 приведен пример графического сглаживания наблюденного поля и выделения плавно изменяющегося регионального поля и локальной аномалии: Δgлок = Δgнабл – Δgрег (подробнее см. 1.4.2).
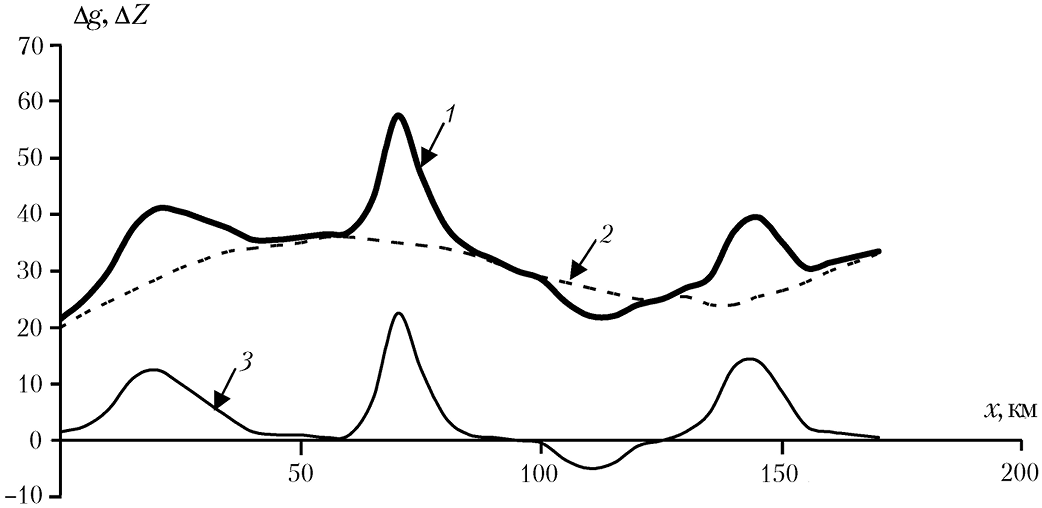
Рис. 1.2. Наблюденные (1), региональные (2) и локальные (3) аномалии силы тяжести
Плотность (σ) служит единственным физическим параметром горных пород и руд, участвующим в создании аномалий силы тяжести. Плотность, т. е. масса единицы объема породы σ = m/V в системе СИ имеет размерность килограмм на кубический метр, но нередко указывают размерность в системе СГС — грамм на кубический сантиметр. Обычно измеряют плотность образцов, взятых из естественных обнажений, скважин и горных выработок. Самый простой способ определения плотности образца состоит в его взвешивании в воздухе и в воде. На этом принципе построен денситометр — прибор, позволяющий определять σ с погрешностью 0,01 г/см3. Но наиболее надежные и правильные данные о плотности горных пород получают при измерениях в естественных условиях залегания, для чего используют наземно-скважинные гамма-гамма или подземный мюонный методы.
Плотность горных пород и руд главным образом зависит от химико-минерального состава и пористости. Плотность изверженных и метаморфических пород определяется в основном минеральным составом и увеличивается при переходе от пород кислых к основным и ультраосновным в соответствии с увеличением железосодержащих минералов. Для осадочных пород плотность определяется прежде всего пористостью, водонасыщенностью и в меньшей степени минералогическим составом. Некоторые значения плотности приведены в табл. 1.1.
Из теории аномального гравитационного поля следует, что изменение (аномалия) силы тяжести обусловлено объемом возмущающего геологического объекта, глубиной его залегания и величиной так называемой избыточной, или эффективной, плотности (Δσэф), представляющей собой разность плотности пород аномалообразующего объекта (структуры) и вмещающих пород:
Δσэф = σстр – σвм. (1.16)
В зависимости от геологической обстановки эффективная плотность (Δσэф) обычно изменяется в пределах нескольких десятых грамма на кубический сантиметр и может быть как положительной, так и отрицательной. Например, разница значений плотности между кристаллическим фундаментом и осадочным комплексом и соответствующий перепад плотности на границе поверхности фундамента составляет 0,1–0,3 г/см3. Примерно такие же значения избыточной плотности наблюдаются и при внедрении интрузий основного состава в осадочный чехол. Одна из самых резких плотностных границ находится между земной корой и мантией (граница Мохоровичича), где фиксируется перепад плотности 0,3–0,6 г/см3. Избыточная плотность соленосных пород по отношению к вмещающим осадочным породам составляет около –0,2 г/см3, что предопределяет возникновение над соляными куполами отрицательных аномалий силы тяжести.
Таблица 1.1. Плотность некоторых веществ, пород, минералов и оболочек Земли
|
Вещество, порода, минерал |
σ, г/см3 |
Вещество, порода, минерал |
σ, г/см3 |
|
Нефть |
0,8–1,0 |
Габбро |
2,8–3,1 |
|
Вода |
1,0 |
Базальт |
2,7–3,2 |
|
Уголь |
1,1–1,4 |
Перидотит |
2,8–3,4 |
|
Почва |
1,13–2,0 |
Эклогит |
3,35–4,2 |
|
Песок |
1,4–1,7 |
Медный колчедан |
4,1–4,3 |
|
Глина |
2,0–2,2 |
Магнетит, гематит |
4,9–5,2 |
|
Песчаник |
1,8–2,8 |
Верхняя часть земной коры (средняя) |
2,67 |
|
Известняк |
2,3–3,0 |
||
|
Гранит |
2,4–3,0 |
Земля (средняя) |
5,52 |
|
Гнейс |
2,6–2,8 |
Ядро Земли |
12,0 |
Теоретически и практически интенсивность аномалий силы тяжести (ΔgБ) oт геологических объектов составляет от долей до первых десятков миллигал (10–5–10–7 от абсолютного значения силы притяжения Земли). Поэтому в гравиразведке для выявления таких тонких гравитационных эффектов от геологических структур разработаны специальная высокочувствительная аппаратура и методика полевых работ.

