• Le plan est un ensemble infini de points.
• Toute droite (1) est une partie propre du plan. Elle possède une infinité de points.
• Par deux points distincts du plan, il passe (2) une droite et une seule; cette droite est contenue dans le plan.
• Un point du plan étant (3) fixé:
il existe (2) une infinité de droites du plan passant par ce point;
il existe une infinité de droites du plan ne passant pas par ce point;
• Deux droites distinctes ont au plus un point commun.
• Des points sont dits alignés s’ils appartiennent à une même droite.
Représentation et notation
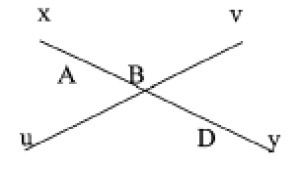
Sur la figure 1, les notations (AB), D, (x y), désignent la même droite:
(AB) = D = (x y).
Les points A et B sont des éléments de la droite D:
A ∈ D; B ∈ D.
Le point B est commun aux droites distinctes (x y) et (u v):
(x y) ∩ (u v) = {B}.
Les points distincts A et B forment une paire de points de D:
{A, B} ⊂ D.
Vocabulaire:
|
plan (m) |
плоскость |
|
partie (f) |
часть; подмножество |
|
propre, – |
собственный |
|
infinité (f) |
бесконечность |
|
passer par qch |
проходить через что-л. |
|
contenu, -e |
содержащийся |
|
alignés, -es |
находящиеся на одной прямой |
|
au plus |
самое большее, не более |
|
représentation (f) |
изображение |
|
notation (f) |
обозначение |
Des éléments de grammaire de texte:
Des substituts:
cette (droite), ce (point).
Hiérarchiser:
– N.B. Pour formuler la conclusion, condensez le contenu du texte en 1–2 phrases. (Для того, чтобы сформулировать заключение, обобщите содержание текста в 1–2 фразах).
Exemple: En bref, on peut dire que les droites du plan...
Révision de la grammaire de base:
(1) Tout, -e – «всякий, каждый».48
(2) Il passe (une droite)... – глагол “passer” в безличной конструкции переводится: «проходит (прямая)...».
(3) Etant fixé – причастие пассивной формы глагола “être fixé”, употребленное в абсолютной конструкции, переводится придаточным предложением: «Когда (если) выбрана точка на плоскости, то...».49

