1. Parallélogrammes
|
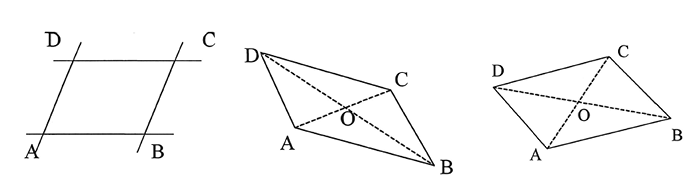
Un quadrilatère est un parallélogramme si, et seulement si: • les supports de ses côtés sont parallèles deux à deux (fïg. 7), • ses diagonales ont même milieu (fig. 8). |
Autres propriétés
• Tout parallélogramme admet un centre de symétrie: le milieu commun des deux diagonales (fig. 9).
• Les côtés opposés d’un parallélogramme ont même longueur (fig. 9).
|
fig. 7 |
fig. 8 |
fig. 9 |
|
(AB) //(CD) { (AD) //(BC) |
OB=OD; OA=OC synonyme de ABCD est un |
Si ABCD est un |
2. Losanges
|
Un quadrilatère est un losange si, et seulement si: • ses quatre côtés ont la même longueur; ou bien • c’est un parallélogramme dont deux côtés consécutifs ont la même longueur; ou bien • c’est un parallélogramme dont les supports des diagonales sont perpendiculaires; ou bien • les supports des diagonales sont des axes de symétrie. |
Vocabulaire:
|
quadrilatère (m) |
четырехугольник |
|
support (m) |
опора, зд. носитель |
|
deux à deux |
попарно |
|
diagonale (f) |
диагональ |
|
symétrie (f) |
симметрия |
|
opposé, -е |
противоположный |
|
consécutif, -ve |
последовательный, зд. соседний |
|
axe (m) |
ось |
Lecture de formules et de symboles:
voir la description des dessins.
Des éléments de grammaire de texte:
Des articulateurs et des substituts:
a) si et seulement si, ou bien, alors;
b) dont.
Hiérarchiser:
– N.B. Dans l’introduction énumérez tous les points que vous allez développer dans la partie principale. (Во введении перечислите все пункты, которые вы собираетесь развивать в основной части).
Exemple: Dans ce texte on envisage les notions ci-dessous: a), b), c) etc.

