Texte 2. Vocabulaire de la géométrie. Suite

• Triangles.

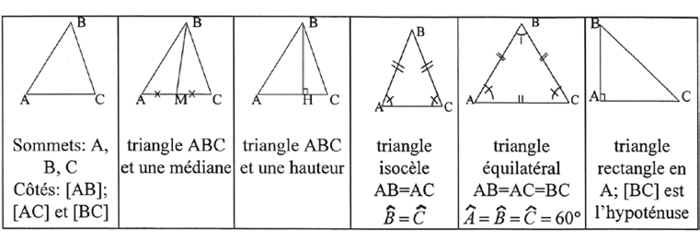
Les trois médianes d’un triangle sont concourantes en un point appelé centre de gravité du triangle.

Les trois hauteurs d’un triangle sont concourantes en un point appelé orthocentre du triangle.

• Parallélogrammes.

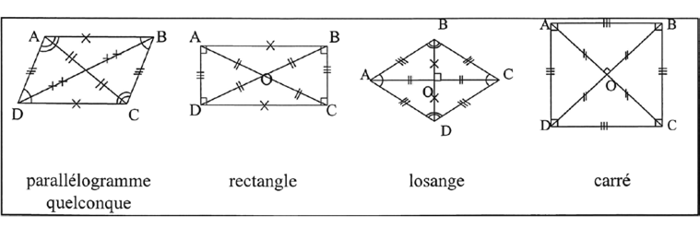
• Trapèzes.

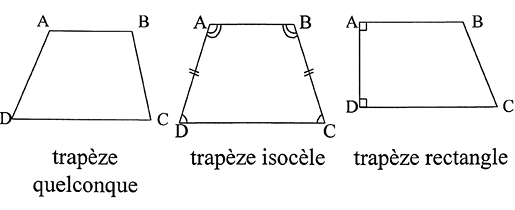
• Cercle – Disque – Arc.

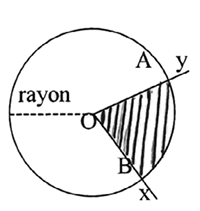
[Ox, Oy] secteur angulaire au centre intercepte l’arc AB. La partie hachurée est secteur de disque

• Objets géométriques. Grandeurs. Mesures

Vocabulaire:

suite (f)	продолжение
triangle (m)	треугольник
sommet (m)	вершина
côté (m)	сторона
médiane (f)	медиана
hauteur (f)	высота
isocèle, -	равнобедренный
équilatéral, -e	равносторонний
rectangle	прямоугольный
hypoténuse (f)	гипотенуза
concourant, -e	сходящийся в одной точке
gravité (f)	тяжесть; сила тяжести
centre de ~	центр тяжести
orthocentre (m)	ортоцентр
parallélogramme (m)	параллелограмм
losange (f)	ромб
carré (m)	квадрат
trapèze (m)	трапеция
cercle (m)	круг, окружность
disque (m)	диск, круг
arc (m)	1) дуга 2) арка
rayon (m)	радиус
intercepter qch.	отсекать
arc intercepté par un	Дуга,
secteur angulaire au	соответствующая
centre	центральному углу
hachurer qch.	заштриховать ч.-л.
grandeur (f)	величина
mesure (f)	мера
être (m)	существо
surface (f)	поверхность
longueur (f)	длина
aire (f)	площадь
amplitude (f)	амплитуда, размах
unité (f)	единица
degré (m)	градус
grade (m)	град, градус десятичный (часть прямого угла)

Des éléments de grammaire de texte:

– Attention aux sous-titres ( • Triangles etc.): ils peuvent être mentionnés non seulement au développement, mais aussi à l’introduction.

Французский язык для математиков