Государственное управление Российской Федерации: вызовы и перспективы

Лавренова Е.В., Смольникова И.А.* (Россия, г. Москва)

Аннотация. С целью оценки влияния инноваций на успеваемость сформулированы типовые гипотезы для статистической обработки результатов обучения. Предложены соответствующие статистические критерии и примеры для подтверждения или опровержения гипотез на уровне статистической значимости для возможного переноса результатов с конкретной выборки на всю генеральную совокупность. Дано сравнение критериев и программ, алгоритм их применения. Статистически значимые выводы являются обоснованием для последующего внедрения новшества и моделирования корректирующих воздействий с целью повышения результативности обучения. Технологию сравнения можно использовать не только в образовательном процессе, но и в аналогичных социально-экономических акциях.

Развитию познавательной, поведенческой и конструктивной компетентности учащегося и компонентам профессиональной деятельности педагога, методиста и администратора для 3-х типов ориентации педагогического процесса в условиях информатизации посвящена работа [1]. Современные и перспективные достижения автоматизации посредством информационных и коммуникационных технологий (ИКТ) учебного процесса рассмотрены в [1]. Большинство преподавателей разрабатывает (или адаптирует готовые) электронные образовательные ресурсы.

Для практикума управленцев по ИКТ автором разработан набор компьютерных моделей по различным аспектам менеджмента, а также тиражируемая методика обучения их совершенствованию для практического использования в дальнейшей работе менеджеров [4]. Профессиональные информационные и коммуникационные инструменты менеджера и их освоение при обучении рассмотрены в [5]. Методические материалы (в том числе, методика разработки электронных учебно-методических комплексов, конструктор для самообучающих лекционных тестов [2] и инструкция для разработки Интернет-теста и его автоматической проверки для контроля готовности [3]) автора доступны всем преподавателям.

Но до внедрения новшества (программы новых курсов, новые учебно-методические материалы, инновационные технологии обучения) проводят их апробацию. При проведении педагогического эксперимента (ПЭ) необходимо показать, что, будучи примененными к объекту (например – к группе обучаемых), новые методики, средства, способы обучения дают лучшие результаты, чем применение традиционных педагогических воздействий [6; 7].

При апробации новых средств и методов обучения надо следовать теории педагогического эксперимента. Для объективности выводов о результатах педагогических новаций необходимо корректное сравнение результатов использования традиционных и инновационных методик. Оно возможно лишь в рамках специально поставленного ПЭ. Этапы современного педагогического исследования рассмотрены в [6–8]. Последуем им (см. п. I ниже) как в предшествующем эксперименте [10]. Взяты те же данные (табл. 1 ниже), но в [10] они были обработаны без использования статистических программ, а теперь – с их применением.

I. Педагогический эксперимент

1. Две группы

Из учебного потока или его части (например, специализации) выделяются экспериментальная (училась по инновационной методике) и контрольная (обучалась традиционными средствами) группы обучаемых. Были фиксированы аналогичные группы прошлого (контрольная) и нынешнего (экспериментальная) года (вел один преподаватель), а также группы 2-х специализаций (контрольная и экспериментальная) нынешнего года (параллельно вели 2 преподавателя). Проведенные входные тесты дали снижение экзаменационных оценок предшествующего близкого курса за счет разрыва во времени и, как следствия, забывания знаний и снижения нужных умений (левые столбцы групп в табл. 1 ниже).

2. Измерительная шкала

Выбор методов обработки результатов зависит от того, в какой измерительной шкале производились измерения [7, 8]. Измерительная шкала – это числовая система, в которой отношения между различными свойствами изучаемых явлений, процессов переведены в свойства множества, удобнее – чисел. В педагогике используются два типа шкал – порядковая (ранговая, например, «зачет» – «незачет» или традиционные оценки «2» – «5») и шкала отношений (баллы от 0 до максимально возможного, например, 100 – на ЕГЭ). Для сохранения степени различия групп, учитывая мощность (см. табл. 2 в [10]) шкалы измерения, лучше не спускаться («отношения» > «порядка» > «наименований») на нижний уровень до группировки в интервалы и категории. Но т.к. входные тесты оценивались традиционными оценками, то пришлось и бальную систему курса в итоге огрубить до оценок «2» – «5».

Результаты входного и выходного тестов приведены в табл. 1 (табл. 5 в [10]):

Таблица 1

Оценки групп студентов, участвующих в ПЭ

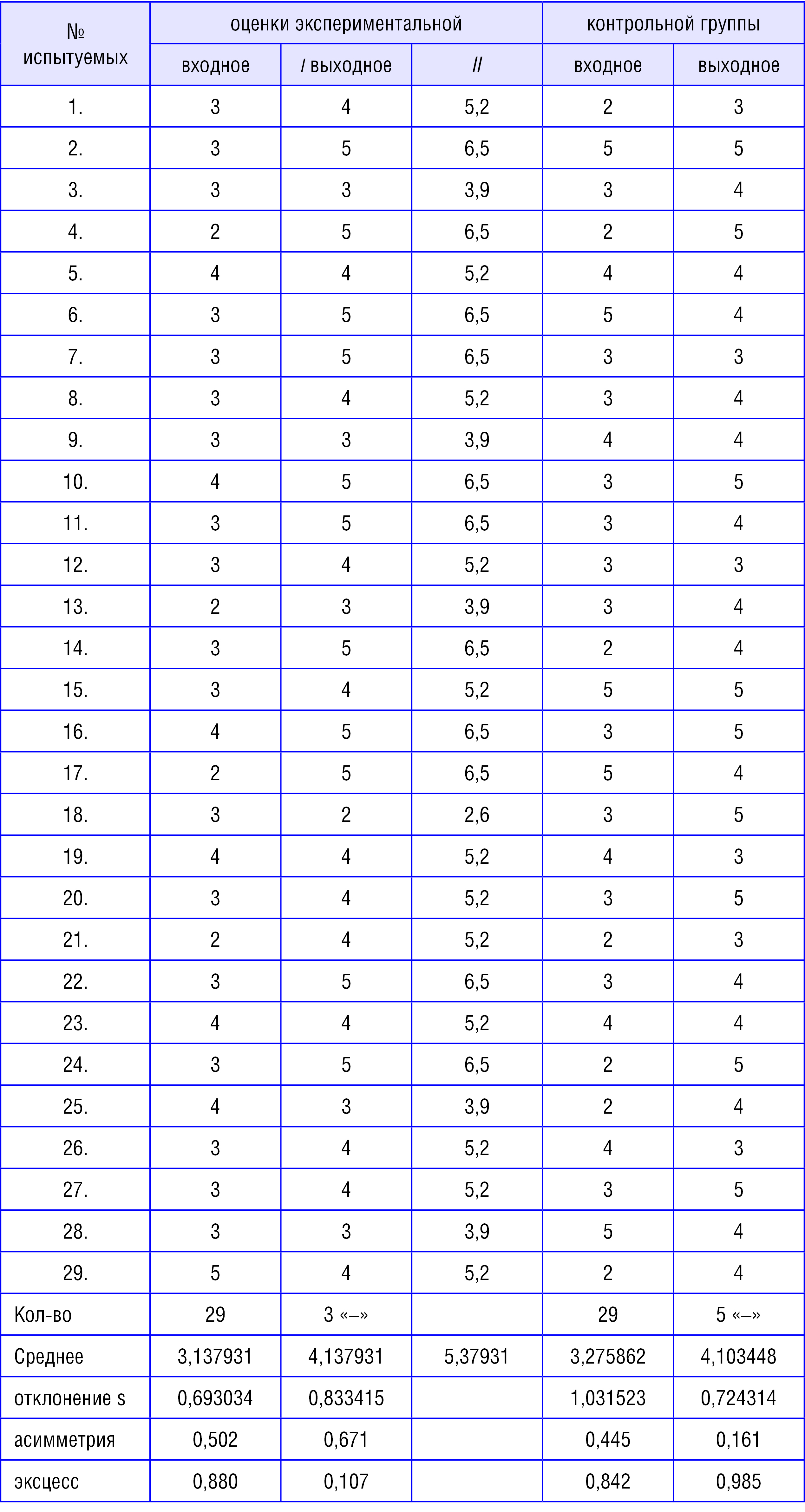
Сравним (п. 3–6 ниже) оценки 2-х групп учащихся – 5 столбцов числовых результатов:

1. экспериментальная (по новому курсу, технологиям и методике) и
2. контрольная (по традиционному курсу, технологиям и методике) по

   a) входным (до начала обучения) и

   b) выходным (по итогам обучения – традиционно I и с повышающим коэффициентом II).

3. Описательная статистика и визуальная разведка

При обработке результатов ПЭ используются обобщающие статистические показатели выборки (столбца оценок конкретных учащихся): среднее значение и стандартное отклонение σ, асимметрия и эксцесс – см. в 4-х нижних строках табл. 1.

Вычислять показатели можно и вручную, но в ПО Statistica они выдаются вместе с удобной визуализацией. Эти показатели используются для наглядного представления и первичного анализа результатов измерений экспериментальной и контрольной групп. Каждому столбцу соответствует свой «ящик с усами» – разброс данных относительно медианы или средне группового значения.

Но сначала проверим нормальность распределения частот одинаковых оценок (сводная таблица) по их гистограмме: везде 1 горб в центре – см. рис. 1:

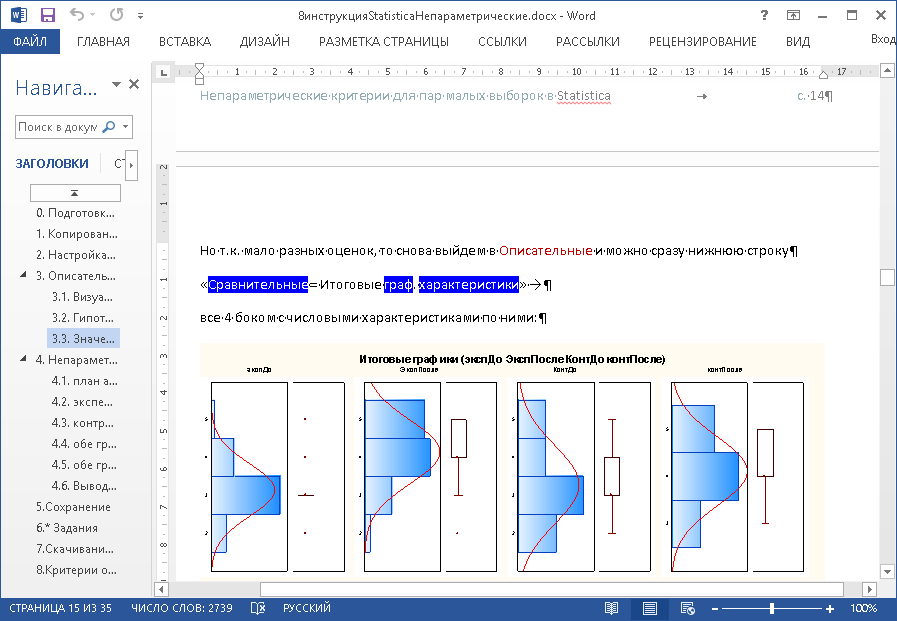
Рис. 1. Отклонения гистограмм от нормального распределения

Далее, т.к. асимметрия и эксцесс (см. последние строки табл. 1) по модулю <1 (из допустимых 3), то отклонения гистограмм от нормального распределения незначительные и возможно в дальнейшем использование статистических критериев для сравнения (см. п.5 ниже).

Сначала сравним средние значения (точки в середине) и отклонения от них –см. рис. 2:

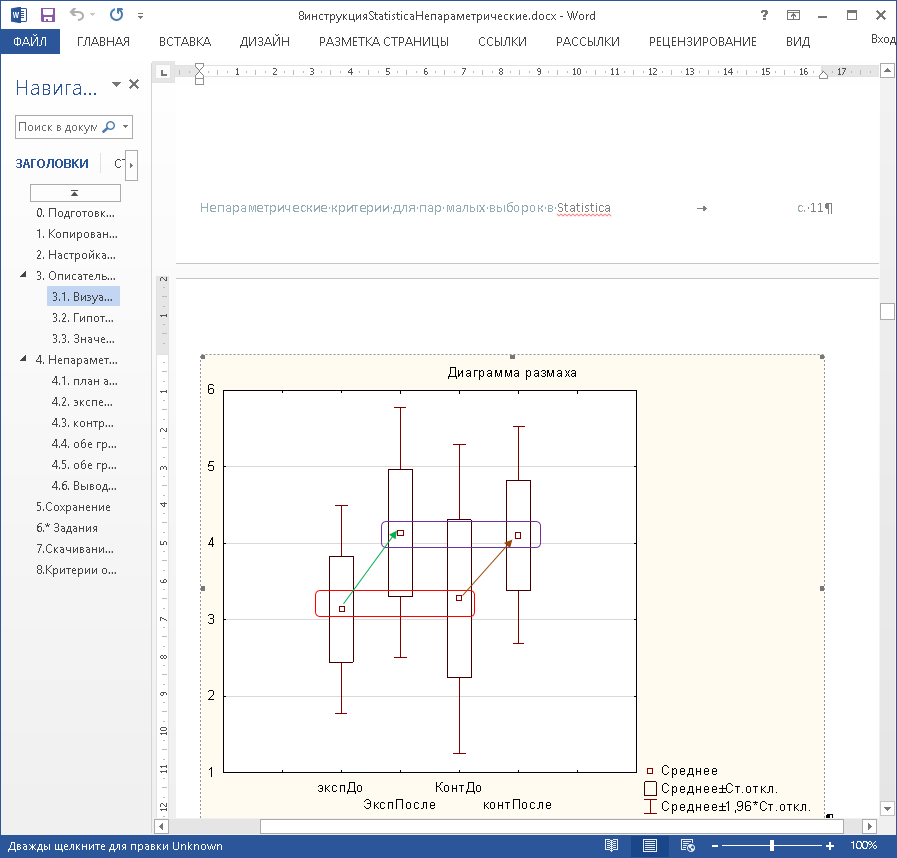
Рис. 2. Сравнение средних значений и отклонения от них

В отличие от средних (см. рис. 2) медианы (см. рис. 1) располагаются внизу ящика, но соотношения между ними одинаково.

4. Гипотезы

По п.3 выдвигаются гипотезы. Видим для средних результатов конкретных учащихся – см. на рис. 2 (выше):

1. примерно равный уровень групповых средних на входе «до» (1 и 3-я), что значит равные стартовые условия эксперимента;
2. в обоих группах «до» ниже (меньше), чем на выходе «после» (1 и 2-я) и (3 и 4-я), что значит улучшение в каждой группе «после»;
3. но расстояние (длина стрелки) в экспериментальной больше, чем в контрольной:

из 4-й снизу строки таблицы 1 (выше): разность средних «до» и «после» в экспериментальной =1 – это больше, чем в контрольной = 0,83 → улучшение в экспериментальной значительнее, да и разброс (стандартное отклонение) невелик.

Так как объектом ПЭ являются люди и количество случайных факторов, влияющих на результаты обучения, велико, то о различии характеристик групп судят на основе вероятностных заключений. Задача анализа первичных данных ПЭ – определение степени достоверности совпадений и различий интегральных характеристик экспериментальной и контрольной группы. После обучения результаты групп должны быть односторонне различными, а до обучения входные – схожими.

Для этого формулируется нулевая гипотеза Н0 – считается, что на заданном уровне значимости α значения сравниваемых столбцов совпадают (с вероятностью 1–α). Если Н0 статистически не значима (α > 0,05), то рассматривается альтернативная гипотеза Н1 о значимости различий (с вероятностью 1–р) – см. пример ниже.

5. Статистические критерии

Для принятия решений о том, какую из гипотез следует принять, используют статистические критерии. По формуле выбранного критерия на основе результатов наблюдений вычисляется число, называемое эмпирическим значением критерия. Это число сравнивается с известным (заданным таблично) числом, называемым критическим значением критерия для фиксированного α ≤ 0.05. Если полученное эмпирическое значение критерия оказывается меньше или равно критическому, то принимается Н0 В противном случае, если эмпирическое значение критерия оказывается больше критического, то нулевая гипотеза отвергается и принимается альтернативная гипотеза Н1 о значимости различий характеристик с 1–р.

По результатам сравнения (знак неравенства) либо принимается Н0 на уровне значимости α (вероятности ошибки отбрасывания верной гипотезы Н0), либо Н1 с достоверностью 1–р. Для односторонних различий (не просто «≠», а «>») надо проверять неравенство с модулем вычисленного (эмпирического) значения – см. примеры в I ниже. При этом надо учесть зависимость либо независимость выборок:

1. зависимые – результаты входного и выходного тестирования одних и тех же учащихся
2. независимые – результаты однотипного тестирования учащихся разных групп.

Обзор назначения критериев статистической обработки результатов обучения дан в [6–8 и 10]. Но т.к. длина выборок N = 29 < 50, то правомерны только непараметрические критерии.

Таблица 2

Сводная таблица вероятностей 1–р соответствующих критериев в Statistica

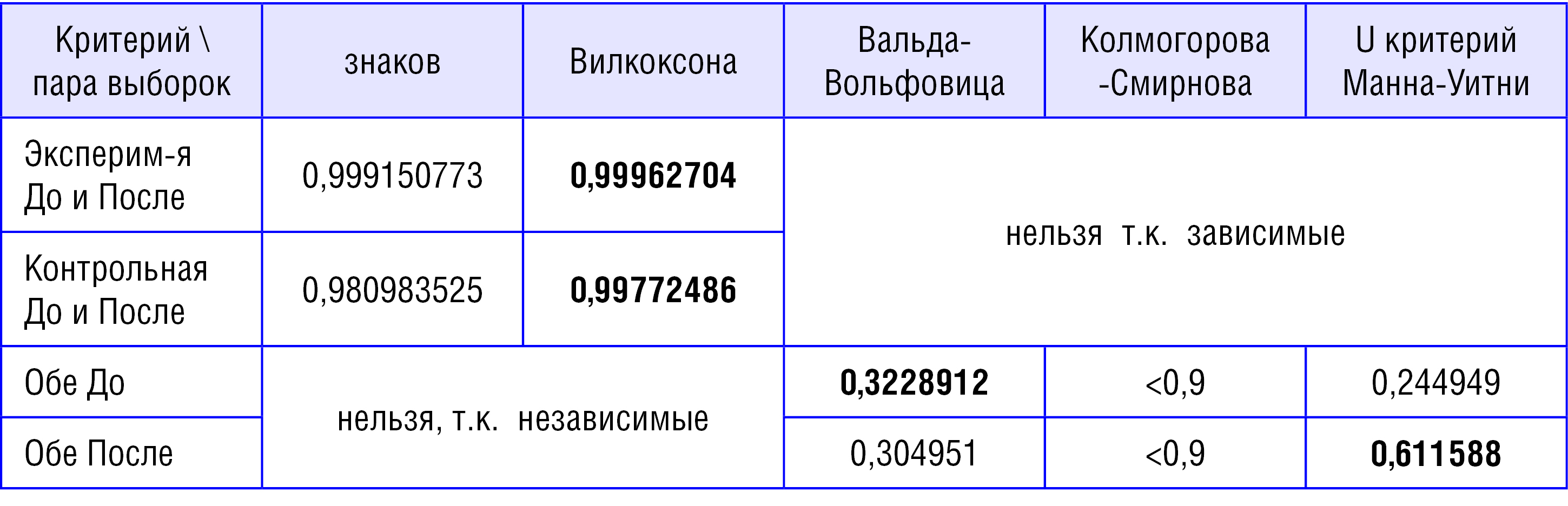
Сводная таблица параметров критериев с гипотезой и ее вероятностью по более чувствительному критерию (жирным выделено максимальное значение в строке):

Вилкоксона – для 2-х первых строк, а для 2-х последних строк соответственно Вальда-Вольфовица – для 3-й и Манна-Уитни – для 4-й:

Таблица 3

Сводная таблица с гипотезой и ее большей вероятностью из таблицы 2

6. Интерпретация выводов

Можно ли результаты конкретных учащихся пар сравниваемых групп перенести на всех учащихся в аналогичных условиях? По табл. 3:

1. Отличие пары уровней средних до (3-я строка) статистически не значимы (<0,95), поэтому считаем, что входной уровень статистически «схож», что означает равные условия начала эксперимента.
2. В обоих группах до обучения уровень ниже (меньше), чем после (1 –я и 2-я строки), что значит улучшение после, причем в каждой группе улучшение статистически значимо (с вероятностью более 0,99);
3. Хотя улучшение в экспериментальной группе больше, чем в контрольной, но отличия средних после (4-я строка) велико, но статистически не значимо, т.е. утверждать, что экспериментальная методика даст улучшение и для других учащихся в аналогичных условиях нельзя.

Итог: Несмотря на «чистоту» эксперимента (п.1) и его положительные результаты (п.4) гипотеза о значительном улучшении знаний с использованием экспериментальных методик по табл. 3 не подтвердилась.

Однако, если учтем увеличившееся на 4 из 15 количество изученных вопросов и технологий, а также выросшую сложность итогового задания (т.е. 5 из 15), и применив получившийся вес (*1,3) к столбцу I табл. 1 (выше) для учета этих факторов, то баллы экспериментальной группы после обучения увеличатся (столбец II) и прирост успеваемости в экспериментальной группе станет значимо выше, чем в контрольной. Теперь гипотеза (3’) о значительном улучшении уровня знаниево-деятельностной компоненты готовности экспериментальной группы по сравнению с контрольной после ПЭ подтвердилась статистически значимо (с вероятностью более 0,98).

Для оперативности и массовости проверки знаний использованы тесты:

в лекционной презентации на основе конструктора [2],

в Googl-форме на сайте на основе инструкции [3].

В будущем в качестве наилучших измерений следует применять задания со свободным конструированием ответа при применении автоматизированного контроля, используя для этого многомерную вероятностную модель процесса решения задачи, а также факторный анализ [7].

II. Сравнение критериев

1. Критерий знаков: ручной в [10] (см. в табл. 4 ниже) и автоматический в ПО «Statistica» (см. в табл. 2 выше).

Вычисляются только знаки и их количество (в 5-й снизу строке табл. 1) или сами «сдвиги» и суммы нулевых, положительных и отрицательных сдвигов экспериментальной и контрольной групп. С помощью табл. 7 в [10] оценивался уровень различий входного и выходного тестирования. Результат для экспериментальной группы усилился: улучшение с вероятностью не 99%, а 99,9%.

А для контрольной группы результат уточнился: общий положительный сдвиг статистически не достоверен с вероятностью 95% (при грубом ручном оценивании), но достоверен с вероятностью 77% (при точном автоматическом оценивании).

2. В Statistica (см.ниже) реализован критерий Манна-Уитни, но не реализован вариант, уточненный Вилкоксоном (ВМУ). А результаты по ним различны: критерий Манна-Уитни дал повышение итоговых результатов в экспериментальной группе только на 37,6% по сравнению с контрольной, а ВМУ, рассчитанный вручную в [10] – 95%.

Т.о., с достоверностью не ниже 95% значение результатов выполнения тестовых заданий для исследования знаниевой компоненты профессиональных компетенций в экспериментальной группе (даже без повышающего коэффициента) будет выше, чем в контрольной группе студентов, обучающихся в сходных с нашими студентами условиях.

Видим, что ручной критерий знаков груб, а ВМУ более чувствительный. Сравним вероятности, полученные параметрическими методами в Excel:

Таблица 4

Продолжение таблицы 3 для параметрических методов и их вероятностей

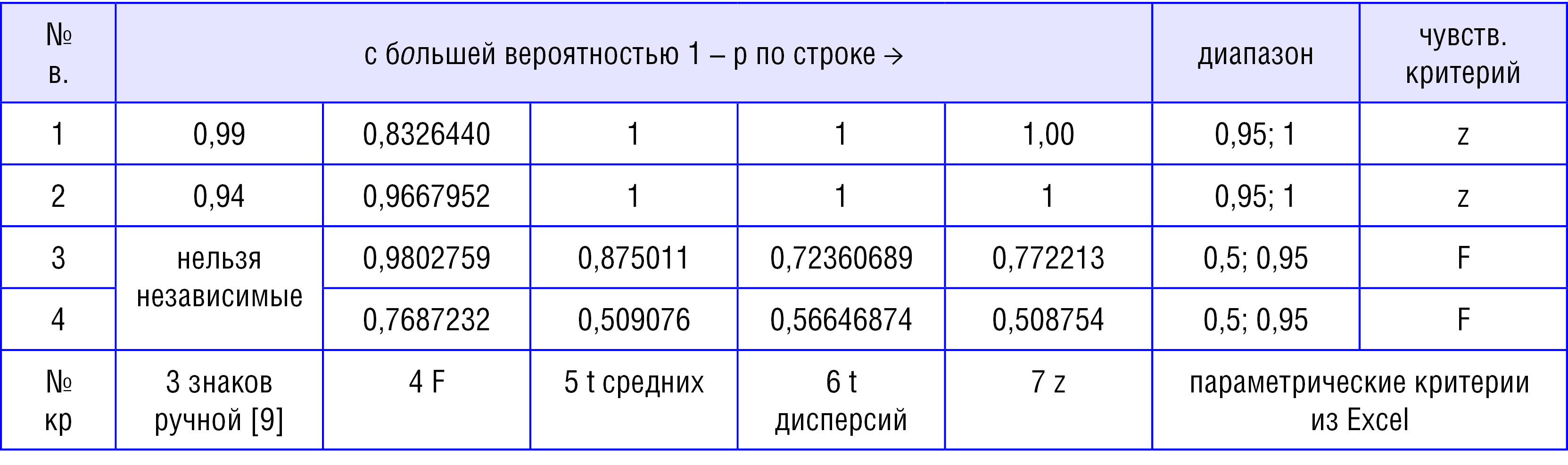
Выводы по критериям сравнения пар выборок:

Т.к. длины выборок < 50, то параметрические критерии не правомерны. Непараметрические критерии (табл. 2 выше) дали ожидаемо худший результат (меньшую вероятность даже для самого чувствительного критерия), но для имеющихся данных выводы в части принятия или отклонения гипотезы Н0 совпадают.

В рассмотренном примере данные критичны: попытка сблизить результаты экспериментальной и контрольной групп при сохранении различия средних баллов не дадут статистически достоверных различий.

Выводы по технологиям обработки результатов эксперимента:

Если длины пары выборок <50, то нужно сразу использовать непараметрические критерии в Statistica, причем выбирать самый чувствительный:

Вилкоксона – для 2-х зависимых выборок, и любой (Вальда-Вольфовица или Манна-Уитни) – для 2-х независимых выборок, можно даже разной длины.

Если сумма объемов выборок >100, то нужно сразу использовать параметрические критерии (табл. 4 выше), причем для зависимых выборок лучше использовать z-критерий, а для независимых – F-критерий.

Выводы будут статистически значимы при 1– р > 0,95; поэтому нужно начать с α = 0,05. Далее:

1. в случае статистической значимости Н0 попробовать уменьшить α. Остановиться в случае статистической значимости Н0 на самом маленьком α.
2. в случае статистической незначимости Н0 попробовать увеличить α. Остановиться в случае статистической значимости Н0 при самом маленьком α < 0.5. Если р < 0.5, то принять H1 с вероятностью 1– р. Если р < 0.05, то H1 статистически значима.

Именно для распространения выводов с конкретных студентов на всех обучающихся в схожих условиях (генеральная совокупность) и применяют продемонстрированный аппарат математической статистики.

Отметим, что использование статистических методов требует планировать педагогический эксперимент на стадии его подготовки, оценивать необходимый объем выборок, их зависимость или независимость, шкалу измерений и другие важные параметры.

III. Статистические компьютерные программы для автоматизации расчетов

Для описательной статистики можно использовать бесплатную программу WolframAlpha с ручным вводом данных. Для педагогических экспериментов можно использовать бесплатную программу PedStat (www.mtas.ru/uploads/stst.zip) [8].

Для начала сравнения выборок (в виде столбца) достаточно возможностей модуля анализа распространенной универсальной программы MS Excel – описательная статистика, которая при выделении выборок сразу выдаст их индивидуальные харатеристики: среднее, стандартная ошибка, медиана, мода, стандартное отклонение, дисперсия выборки, эксцесс, асимметричность, интервал, минимум, максимум, сумма, счет (количество), уровень надежности (для 95,0%).

Но в широко распространенной MS Excel пока выше названные непараметрические критерии не реализованы, а реализованы только параметрические методы.

Следует заметить, что реализованный (в аналитическом модуле MS Excel) критерий «χ2 согласия» отличается от рекомендованного «χ2 однородности», поэтому следует набрать формулы самостоятельно или пользоваться:

1. бесплатными настройками к Excel в Интернете: Megastаt, XLStat
2. более мощными, но дорогими и непростыми в освоении профессиональными статистическими пакетами: SPSS, STATGraphics, Statistica (русифицирована).

Работа в Statistica, Genehunter, FuzzyXl с примерами для экономических и социологических исследований, когда число факторов велико, в том числе, с разбором неправильного применения и неверными выводами, рассмотрена в [8].

Непараметрические критерии реализованы только в Statistica, хотя без более чувствительного критерия Вилкоксона-Манна-Уитни (ВМУ).

Вывод

Большие возможности и далекие перспективы использования ИКТ требуют не только готовности всего коллектива создавать информационные ресурсы и использовать информационную среду, но и оперативной обратной связи, анализа результатов для повышения эффективности образовательной, профессиональной, научной и административной деятельности. Для обработки экспериментальных данных в МГУ для научно-педагогических работников проводятся межфакультетские курсы по закупленной специализированной статистической и Data Mining – программе Statistica, но пока без педагогической составляющей. Для представленного способа доказательства статистической значимости инновации авторами разработана подробная инструкция для обработки первичных педагогических данных в модуле анализа MS Excel и Statistica. Поэтому желающие смогут получить поддержку как очно, так и дистанционно. Предъявленный способ доказательства может быть распространен на данные социально-педагогических экспериментов в интервальной шкале (см. п.2 в I).

Список литературы

1. Смольникова И.А. Развитие информационных и коммуникационных систем обучения. // Гос. управление в XXI веке: традиции и инновации: Матер. 8-й междунар. конференции. – ФГУ МГУ имени М.В. Ломоносова, 2010. Ч. 1. – С.739–746.
2. Смольникова И.А. Разработка интерактивной тестирующей презентации (сайта) на основе конструктора (шаблона) // Информатика и образование, 2008. №8. – С. 25–29 (2009. №2. С. 63–68).
3. Смольникова И.А. Конструирование обучающе-контролирующего google – сайта и методика его использования. // Применение новых педагогических технологий: Матер. 26-й Межд. конференции-выставки. – М.: Троицк, 2015. Секция 1. – C. 132–133.
   URL: http://ito.mosedu.ru/files/materials.pdf (29.05.2016).
4. Смольникова И.А., Мартынов Ю.В. Интеграция компьютерного моделирования управления для обучения и практического использования. // Гос. управление в XXI веке: традиции и инновации: Матер. 7-й междунар. конференции. ФГУ МГУ имени М.В. Ломоносова, 2009. Ч. 3. – С. 647–656.
5. Смольникова И.А., Мартынов Ю.В. Информационные и коммуникационные инструменты менеджера и их освоение при обучении. // Гос. управление в XXI веке: традиции и инновации: Матер. 7-й междунар. конференции. ФГУ МГУ имени М.В. Ломоносова, 2009. Ч. 3. – С. 656–666.
6. Смольникова И.А. Планирование педагогического эксперимента и статистическая обработка результатов посредством ИТ // Дистанционное образование: проблемы, перспективы развития – М: ФИРО, 2007. – С. 143–159.
7. Грабарь М.И. Измерение и оценка результатов обучения. – М.: ИОСО РАО, 2000. – 93 с.
8. Новиков Д.А. Статистические методы в педагогических исследованиях. – М: М3-Пресс, 2004. – 67 с.
   URL: www.mtas.ru/pedstat.pdf (29.05.2017).
9. Петрунин Ю.Ю. Информационные технологии анализа данных. Data Analysis: учебное пособие. – М.: КДУ, 2008. – 292 с.
10. Лавренова Е.В., Смольникова И.А. Статистические критерии социально-педагогических исследований. // Гос. управление в современном мире: Матер.13-й междунар. конференции. ФГУ МГУ имени М.В. Ломоносова, 2015, секц.VII, с.62–70.
    URL: http://spa.msu.ru/uploads/files/knigi/conf_2015_7.pdf.

---